Z życia muchy

Wipipedia
Zapewne każdy z nas dobrze zna muszkę owocówkę (drosophila melanogaster, co tłumaczy się dosłownie jako ciemnobrzucha miłośniczka rosy). Dla większości ta dobra znajomość niekoniecznie musi budzić dobre skojarzenia – być może z uwagi na jej natrętny muszy charakter i masową obecność letnią porą w pobliżu nieopatrznie zostawionych bez przykrycia słodkich owoców. Niemal równie powszechna jest wiedza o jej zasługach naukowych w dziedzinie genetyki. Mało kto zdaje sobie sprawę z tego, że to nie pies Łajka, a właśnie muszka była pierwszą ziemską istotą, która wybrała się w podróż kosmiczną. Ale czy ktoś uwierzy, że muszka pomogła również w rozwiązywaniu pewnego problemu z pogranicza matematyki i informatyki?
Rys. 1
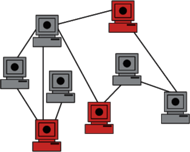
Większość systemów komputerowych, z jakimi mamy obecnie do czynienia, to tak zwane systemy rozproszone, czyli niezależne urządzenia (stosując pewne uproszczenie, będziemy dalej mówić o procesorach) połączone, mniej lub bardziej ściśle, w jedną sieć, mogące się komunikować i sprawiające wrażenie jednej całości. Jednym z kluczowych zadań, przed jakim staje projektant takiego systemu, jest rozwiązanie problemu komunikacji. Ustanowienie bezpośredniego połączenia między każdymi dwoma urządzeniami w sieci byłoby nieefektywne i nieopłacalne, konieczne jest więc wyznaczenie możliwie najmniejszego zbioru procesorów (tak zwanych liderów), który będzie miał bezpośrednie połączenie z każdym procesorem z zewnątrz. Model matematyczny tego zagadnienia najłatwiej jest przedstawić w języku teorii grafów. Zbiór wszystkich komputerów w sieci możemy utożsamiać z wierzchołkami grafu, a strukturę połączeń pomiędzy nimi opisuje zbiór krawędzi tego grafu (Rys. 1).
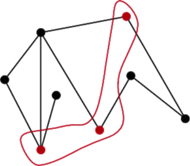
Rys. 2 Minimalny niezależny zbiór dominujący (czyli maksymalny zbiór niezależny) w grafie.
Definicja. Zbiór parami niesąsiednich wierzchołków grafu, w którym swojego sąsiada ma każdy wierzchołek spoza zbioru, a do tego jest nienadmiarowy (czyli jeśli cokolwiek z niego zabierzemy, to przestanie mieć tę pierwszą cechę), w teorii grafów nosi nazwę minimalnego niezależnego zbioru dominującego.
Jest to pojęcie dualne do pojęcia maksymalnego zbioru niezależnego. Maksymalny zbiór niezależny to taki, w którym żadne dwa wierzchołki nie są połączone krawędzią (niezależność) i nie możemy do niego dołożyć nic więcej, żeby własności niezależności nie stracić (maksymalność). Można wykazać, że minimalny niezależny zbiór dominujący jest jednocześnie maksymalnym zbiorem niezależnym i odwrotnie.
Szukanie zbioru liderów w rozproszonej sieci sprowadza się więc do wyznaczenia maksymalnego zbioru niezależnego w reprezentującym ją grafie. Jak znaleźć taki zbiór? Przyjrzyjmy się na początek najprostszym metodom.
Rozwiązanie 1. Ustawiamy wierzchołki grafu w dowolnym porządku. Następnie zgodnie z zadanym porządkiem sprawdzamy, czy kolejne wierzchołki mogą znaleźć się w zbiorze liderów (czy nie mają już w tym zbiorze sąsiada). Jeżeli tak, to dodajemy taki wierzchołek do zbioru.
Rozwiązanie 2. Ustawiamy wierzchołki grafu w dowolnym porządku. Następnie zgodnie z zadanym porządkiem dodajemy wierzchołek do zbioru liderów, natomiast wszystkich jego sąsiadów wyrzucamy z rozważań.
Te najprostsze algorytmy są jednocześnie stosunkowo szybkie. Oba działają
liniowo względem liczby krawędzi. Jednak oba te podejścia mają naturę
sekwencyjną i w związku z tym średnio pasują do modelu systemów
rozproszonych. W 1982 roku znany informatyk-teoretyk Leslie Valiant uznał
problem wyznaczania maksymalnego zbioru niezależnego za jedno z większych
wyzwań informatyki teoretycznej, twierdząc jednocześnie, że trudno
sobie wyobrazić, w jaki sposób ten problem mógłby być rozwiązany
równolegle w istotnie mniejszej liczbie kroków. Trzy lata później A vi
Wigderson i Richard Karp znaleźli skomplikowany algorytm o złożoności
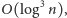 który następnie poprawił zespół pod kierunkiem
Nogi Alona, izraelskiego matematyka i informatyka, uzyskując algorytm
o złożoności
który następnie poprawił zespół pod kierunkiem
Nogi Alona, izraelskiego matematyka i informatyka, uzyskując algorytm
o złożoności
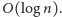

Mamy zatem efektywne algorytmy rozwiązujące problem znajdowania maksymalnego zbioru niezależnego w grafie. W każdym z nich każdy wierzchołek musi znać swoich sąsiadów w grafie, podczas gdy w prawdziwych sieciach mogą występować ograniczenia możliwości komunikacji. Wyobraźmy sobie, na przykład, system kontroli lotu działający w ten sposób, że zrzucamy z samolotu na pewnym terenie tysiące urządzeń monitorujących, które mają się komunikować. Urządzenia mogą jedynie wysyłać sygnały do urządzeń znajdujących się w odpowiedniej odległości. Mamy sieć, którą można reprezentować za pomocą grafu, którego wierzchołki będą odpowiadały urządzeniom, natomiast krawędzie będzie determinowała odległość między nimi. Niestety, urządzenia zostały rozmieszczone na danym terenie w sposób losowy i nie mamy pojęcia, jak wygląda faktyczna struktura sieci. Co możemy zrobić w takim przypadku?
Okazuje się, że natura dawno wymyśliła za nas rozwiązanie tego problemu, a klucz do niego umieściła na głowie muszki owocówki. Ten fakt zaobserwowała oraz opracowała pod kątem matematycznym grupa matematyków i biologów, w skład której wchodzili: Yehuda Afek, Noga Alon, Omer Barad, Eran Hornstein, Naama Barkai i Ziv Bar-Joseph. Wyniki swoich obserwacji zawarli w artykule A biological solution to a fundamental distributed computing problem (Biologiczne rozwiązanie podstawowego problemu obliczeń rozproszonych), który ukazał się w prestiżowym czasopiśmie Science.
Dorosła muszka ma na głowie zespół włoskowatych organów sensorycznych. Kształtują się one jeszcze w stadium larwalnym z sąsiadujących, równorzędnych komórek. Nie ma jednak żadnego klucza, który pomógłby nam wskazać, z których komórek (nazywanych POS-ami) wykształcą się organy sensoryczne. Wiemy natomiast, czym charakteryzują się wybrane już POS-y:
- każda z komórek zostaje POS-em lub sąsiadem POS-a,
- żadne dwa POS-y nie są sąsiadami.
Na głowie muszki tworzy się więc maksymalny zbiór niezależny w grafie komórek – zbiór POS-ów. Poszczególne komórki nie mają informacji, jak wygląda całość struktury. Mogą jedynie wysyłać do swoich sąsiadów sygnał (produkując duże stężenie proteiny Delta), że chcą zostać POS-em. Cały proces trwa około trzech godzin i zawsze kończy się sukcesem. Muszka potrafi zrobić dokładnie to, o co nam chodzi! Algorytm, którego mogliśmy się od niej nauczyć, jest zaskakująco prosty.
Rozwiązanie 3.
- Pewien losowy zbiór komórek wyraża chęć zostania POS-em i wysyła sygnał do wszystkich swoich sąsiadów.
- Każda komórka, która chce zostać POS-em i nie otrzymała sygnału od żadnego ze swoich sąsiadów, zostaje POS-em.
- Każdy POS „usypia” wszystkich swoich sąsiadów.
- Cała procedura powtarza się na zbiorze komórek, które nie zostały jeszcze wybrane na POS-y ani uśpione.
Algorytm ten wykonuje pesymistycznie
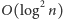 iteracji i z dużym
prawdopodobieństwem łączna liczba wysyłanych w nim sygnałów
jest optymalna (z dokładnością do stałego czynnika). Czytelników
obeznanych z informatyczną terminologią i poszukujących ciekawych
szczegółów odsyłam do wspomnianego wyżej artykułu. Tekstowi,
który ukazał się w czasopiśmie, towarzyszą filmy przedstawiające proces
wyboru POS-ów u muszki oraz dodatek zawierający wszelkie techniczne
szczegóły.
iteracji i z dużym
prawdopodobieństwem łączna liczba wysyłanych w nim sygnałów
jest optymalna (z dokładnością do stałego czynnika). Czytelników
obeznanych z informatyczną terminologią i poszukujących ciekawych
szczegółów odsyłam do wspomnianego wyżej artykułu. Tekstowi,
który ukazał się w czasopiśmie, towarzyszą filmy przedstawiające proces
wyboru POS-ów u muszki oraz dodatek zawierający wszelkie techniczne
szczegóły.