Skojarzenia...
Ten numer Delty jest zdominowany przez tematykę skojarzeń w grafach. Dla
przypomnienia: graf nieskierowany to zbiór wierzchołków połączonych
krawędziami, skojarzenie zaś w tym grafie to taki podzbiór krawędzi
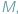 że każdy wierzchołek grafu jest incydentny z co najwyżej jedną
krawędzią z
że każdy wierzchołek grafu jest incydentny z co najwyżej jedną
krawędzią z
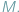
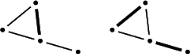
Rys. 1 Po lewej: przykładowe skojarzenie w grafie (pogrubiona krawędź). Po prawej: jedyne najliczniejsze skojarzenie w tym samym grafie.
W wielu zastosowaniach interesować nas będzie wyznaczenie najliczniejszego skojarzenia w grafie, tzn. skojarzenia, które zawiera możliwie najwięcej krawędzi. W tym artykule pokażemy, jak znajdować takie skojarzenia.
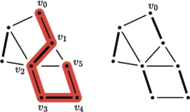
Rys. 2 Graf z wyróżnioną ścieżką powiększającą skojarzenie (kolor) oraz graf po powiększeniu skojarzenia wzdłuż tej ścieżki.
Nasze algorytmy będą działały metodą przyrostową: dla danego grafu
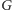 i wyróżnionego w nim skojarzenia
i wyróżnionego w nim skojarzenia
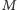 będą znajdować
skojarzenie o jedną krawędź większe bądź też będą stwierdzać, że
będą znajdować
skojarzenie o jedną krawędź większe bądź też będą stwierdzać, że
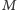 jest już najliczniejszym skojarzeniem. W jaki sposób można
powiększyć skojarzenie? Zauważmy, że jeśli w grafie istnieją dwa
nieskojarzone wierzchołki połączone krawędzią, to można tę krawędź dodać
do skojarzenia. Pomysł ten można uogólnić: jeśli w grafie istnieją dwa
nieskojarzone wierzchołki
jest już najliczniejszym skojarzeniem. W jaki sposób można
powiększyć skojarzenie? Zauważmy, że jeśli w grafie istnieją dwa
nieskojarzone wierzchołki połączone krawędzią, to można tę krawędź dodać
do skojarzenia. Pomysł ten można uogólnić: jeśli w grafie istnieją dwa
nieskojarzone wierzchołki
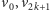 połączone ścieżką, na której
dokładnie co druga krawędź jest skojarzona, tzn. ścieżką
połączone ścieżką, na której
dokładnie co druga krawędź jest skojarzona, tzn. ścieżką
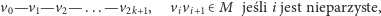 |
to można wyrzucić ze skojarzenia
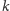 krawędzi
krawędzi
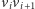 dla
dla
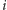 nieparzystego i dorzucić do niego
nieparzystego i dorzucić do niego
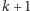 krawędzi
krawędzi
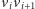 dla
dla
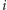 parzystego (Rys. 2). Taką ścieżkę, wzdłuż której powiększamy
skojarzenie, nazywamy ścieżką powiększającą to skojarzenie. Jasne jest, że
jeśli taka ścieżka w grafie istnieje, to możemy powiększyć skojarzenie.
Okazuje się, że implikacja w przeciwną stronę również zachodzi i jest tezą
twierdzenia sformułowanego i udowodnionego przez francuskiego matematyka
Claude’a Berge’a:
parzystego (Rys. 2). Taką ścieżkę, wzdłuż której powiększamy
skojarzenie, nazywamy ścieżką powiększającą to skojarzenie. Jasne jest, że
jeśli taka ścieżka w grafie istnieje, to możemy powiększyć skojarzenie.
Okazuje się, że implikacja w przeciwną stronę również zachodzi i jest tezą
twierdzenia sformułowanego i udowodnionego przez francuskiego matematyka
Claude’a Berge’a:
Twierdzenie. Skojarzenie w grafie jest najliczniejsze wtedy i tylko wtedy, gdy nie istnieje ścieżka powiększająca to skojarzenie.
Tak więc to, czego potrzebujemy, to procedura znajdowania ścieżki
powiększającej lub stwierdzania, że takowa nie istnieje. Dla ustalenia uwagi
możemy skupić się na poszukiwaniu ścieżki powiększającej zaczynającej się
w ustalonym nieskojarzonym wierzchołku
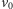 – wystarczy przejrzeć
wszystkie takie wierzchołki. Oczywiście, moglibyśmy wyznaczyć wszystkie
ścieżki wychodzące z tego wierzchołka, korzystając z przeszukiwania
z nawrotami. Taka metoda będzie jednak wymagać czasu wykładniczego, zatem
potrzebujemy czegoś sprytniejszego.
– wystarczy przejrzeć
wszystkie takie wierzchołki. Oczywiście, moglibyśmy wyznaczyć wszystkie
ścieżki wychodzące z tego wierzchołka, korzystając z przeszukiwania
z nawrotami. Taka metoda będzie jednak wymagać czasu wykładniczego, zatem
potrzebujemy czegoś sprytniejszego.
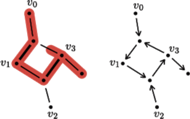
Rys. 3 Graf dwudzielny
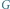 z wyróżnionymi krawędziami odwiedzonymi podczas
przeszukiwania w głąb oraz graf skierowany
z wyróżnionymi krawędziami odwiedzonymi podczas
przeszukiwania w głąb oraz graf skierowany
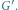 W obu grafach podpisano wierzchołki ze
zbioru
W obu grafach podpisano wierzchołki ze
zbioru
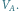
Na początek zajmiemy się grafami dwudzielnymi, tzn. takimi, których zbiór
wierzchołków możemy podzielić na takie dwa podzbiory
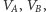 że
każda krawędź łączy wierzchołki należące do różnych podzbiorów.
Spróbujmy usprawnić przeszukiwanie z nawrotami, tak aby odwiedzić
każdy wierzchołek co najwyżej raz. A konkretnie: zaczynając z wierzchołka
że
każda krawędź łączy wierzchołki należące do różnych podzbiorów.
Spróbujmy usprawnić przeszukiwanie z nawrotami, tak aby odwiedzić
każdy wierzchołek co najwyżej raz. A konkretnie: zaczynając z wierzchołka
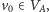 wykonujemy przeszukiwanie grafu w głąb, z tym że
w każdym wierzchołku na głębokości parzystej przeglądamy nieskojarzone
krawędzie wychodzące z tego wierzchołka, w każdym zaś wierzchołku na
głębokości nieparzystej idziemy krawędzią skojarzoną (może być co
najwyżej jedna). Jeśli trafimy na wierzchołek nieskojarzony, to znaczy, że
znaleźliśmy ścieżkę powiększającą (Rys. 3). Co ciekawe, jeśli na niego
nie trafiliśmy, to znaczy, że ścieżki powiększającej nie ma. Jak to
udowodnić?
wykonujemy przeszukiwanie grafu w głąb, z tym że
w każdym wierzchołku na głębokości parzystej przeglądamy nieskojarzone
krawędzie wychodzące z tego wierzchołka, w każdym zaś wierzchołku na
głębokości nieparzystej idziemy krawędzią skojarzoną (może być co
najwyżej jedna). Jeśli trafimy na wierzchołek nieskojarzony, to znaczy, że
znaleźliśmy ścieżkę powiększającą (Rys. 3). Co ciekawe, jeśli na niego
nie trafiliśmy, to znaczy, że ścieżki powiększającej nie ma. Jak to
udowodnić?
Rozważmy graf skierowany
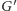 o zbiorze wierzchołków
o zbiorze wierzchołków
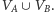 Dla
każdej krawędzi
Dla
każdej krawędzi
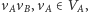
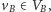 z naszego
z naszego
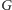 dodajmy
do
dodajmy
do
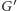 skierowaną krawędź:
skierowaną krawędź:
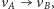 jeśli
jeśli
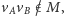 albo
albo
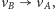 jeśli
jeśli
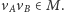 Zauważmy, że w grafie
Zauważmy, że w grafie
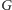 istnieje
ścieżka powiększająca wtedy i tylko wtedy, gdy w grafie
istnieje
ścieżka powiększająca wtedy i tylko wtedy, gdy w grafie
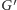 da się
dojść (zgodnie ze skierowaniem krawędzi) z wierzchołka
da się
dojść (zgodnie ze skierowaniem krawędzi) z wierzchołka
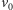 do innego
wierzchołka nieskojarzonego. A powyższy algorytm to nic innego jak zwykłe
przeszukiwanie w głąb grafu
do innego
wierzchołka nieskojarzonego. A powyższy algorytm to nic innego jak zwykłe
przeszukiwanie w głąb grafu
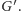
Przeszukiwanie to działa w czasie
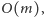 zatem znalezienie ścieżki
powiększającej zajmie czas
zatem znalezienie ścieżki
powiększającej zajmie czas
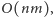 jeśli zaczynamy przeszukiwanie
z każdego wierzchołka nieskojarzonego od nowa, lub
jeśli zaczynamy przeszukiwanie
z każdego wierzchołka nieskojarzonego od nowa, lub
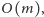 jeśli
zaczynamy naraz z wszystkich wierzchołków nieskojarzonych z
jeśli
zaczynamy naraz z wszystkich wierzchołków nieskojarzonych z
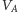 (dlaczego możemy tak zrobić?). Skojarzenie może być powiększone
co najwyżej
(dlaczego możemy tak zrobić?). Skojarzenie może być powiększone
co najwyżej
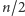 razy, zatem cały algorytm działa w czasie
razy, zatem cały algorytm działa w czasie
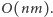 Dodajmy, że w praktyce nie opłaca się zaczynać z pustego
skojarzenia, ale z jakiegoś skojarzenia znalezionego prostszą metodą
(przykładowo, algorytm zachłannie dodający kolejne krawędzie do skojarzenia
zawsze znajdzie skojarzenie o liczności równej co najmniej połowie liczności
najliczniejszego skojarzenia).
Dodajmy, że w praktyce nie opłaca się zaczynać z pustego
skojarzenia, ale z jakiegoś skojarzenia znalezionego prostszą metodą
(przykładowo, algorytm zachłannie dodający kolejne krawędzie do skojarzenia
zawsze znajdzie skojarzenie o liczności równej co najmniej połowie liczności
najliczniejszego skojarzenia).
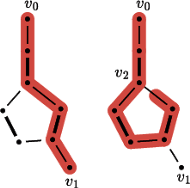
Rys. 4 Po lewej: graf ze skojarzeniem (pogrubione krawędzie) i ścieżką powiększającą (kolor). Po prawej: ten sam graf z krawędziami odwiedzonymi przez algorytm.
Okazuje się, że w przypadku grafów, które nie są dwudzielne, sprawa się
komplikuje, a nasz algorytm nie działa. Istotnie, spójrzmy na graf z rysunku 4
Pomimo tego, że istnieje w nim ścieżka powiększająca z wierzchołka
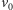 do wierzchołka
do wierzchołka
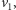 to algorytm nigdy jej nie znajdzie, jeśli
zacznie obchodzić cykl od lewej strony (w szczególności nigdy nie odwiedzi
wierzchołka
to algorytm nigdy jej nie znajdzie, jeśli
zacznie obchodzić cykl od lewej strony (w szczególności nigdy nie odwiedzi
wierzchołka
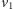 ).
).
Cały kłopot jest powodowany przez cykle, które znajdujemy, przeszukując graf.
Problematyczne okazują się mianowicie cykle nieparzystej długości,
które są połączone z wierzchołkiem
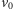 ścieżką o parzystej
długości. Taki cykl nazwiemy kielichem (ang. blossom), a ścieżkę łodygą
(ang. stem). Kanadyjski matematyk Jack Edmonds podał następujący
sposób, w jaki można sobie z nimi radzić: ściągnąć, czyli zastąpić
jednym wierzchołkiem, a następnie rekurencyjnie poszukać ścieżki
powiększającej w mniejszym grafie. Przyjrzyjmy się temu pomysłowi
bliżej.
ścieżką o parzystej
długości. Taki cykl nazwiemy kielichem (ang. blossom), a ścieżkę łodygą
(ang. stem). Kanadyjski matematyk Jack Edmonds podał następujący
sposób, w jaki można sobie z nimi radzić: ściągnąć, czyli zastąpić
jednym wierzchołkiem, a następnie rekurencyjnie poszukać ścieżki
powiększającej w mniejszym grafie. Przyjrzyjmy się temu pomysłowi
bliżej.
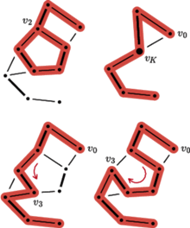
Rys. 5 Na górze po lewej: graf
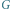 z zaznaczonym kielichem. Na górze po prawej: graf
z zaznaczonym kielichem. Na górze po prawej: graf
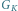 z zaznaczoną ścieżką powiększającą. Na dole: dwie możliwości uzupełnienia
ścieżki powiększającej w grafie
z zaznaczoną ścieżką powiększającą. Na dole: dwie możliwości uzupełnienia
ścieżki powiększającej w grafie
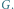
Operacja ściągnięcia kielicha wygląda następująco (Rys. 5): zastępujemy
wszystkie wierzchołki kielicha jednym wierzchołkiem
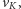 który jest
połączony krawędziami z wszystkimi sąsiadami kielicha, otrzymując graf
który jest
połączony krawędziami z wszystkimi sąsiadami kielicha, otrzymując graf
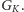 Zauważmy, że na rysunku wierzchołek
Zauważmy, że na rysunku wierzchołek
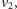 który łączył
kielich z łodygą, był jedynym wierzchołkiem spośród wierzchołków kielicha
skojarzonym z wierzchołkiem poza kielichem, zatem wierzchołek
który łączył
kielich z łodygą, był jedynym wierzchołkiem spośród wierzchołków kielicha
skojarzonym z wierzchołkiem poza kielichem, zatem wierzchołek
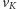 będzie
również skojarzony z dokładnie jednym wierzchołkiem. Wynika z tego, że
po ściągnięciu nowo utworzone skojarzenie
będzie
również skojarzony z dokładnie jednym wierzchołkiem. Wynika z tego, że
po ściągnięciu nowo utworzone skojarzenie
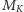 nadal jest poprawne.
Okazuje się, że prawdziwy jest następujący lemat:
nadal jest poprawne.
Okazuje się, że prawdziwy jest następujący lemat:
Lemat. W grafie
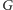 istnieje ścieżka powiększająca skojarzenie
istnieje ścieżka powiększająca skojarzenie
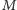 wtedy i tylko wtedy, gdy w grafie
wtedy i tylko wtedy, gdy w grafie
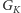 istnieje ścieżka
powiększająca skojarzenie
istnieje ścieżka
powiększająca skojarzenie
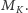
Dla dowodu lematu załóżmy, że w grafie
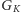 znaleźliśmy
ścieżkę powiększającą
znaleźliśmy
ścieżkę powiększającą
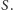 Pokażemy, jak dzięki niej znaleźć
ścieżkę w grafie
Pokażemy, jak dzięki niej znaleźć
ścieżkę w grafie
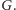 Jeśli ścieżka
Jeśli ścieżka
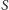 nie zawiera wierzchołka
nie zawiera wierzchołka
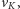 to w oczywisty sposób jest ona również ścieżką powiększającą
w
to w oczywisty sposób jest ona również ścieżką powiększającą
w
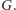 W przeciwnym przypadku można ją uzupełnić krawędziami
z kielicha, przechodząc go w lewo lub w prawo, w zależności od położenia
wierzchołka
W przeciwnym przypadku można ją uzupełnić krawędziami
z kielicha, przechodząc go w lewo lub w prawo, w zależności od położenia
wierzchołka
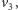 którym wchodzi druga krawędź ścieżki (Rys. 5).
Ponadto każda ścieżka powiększająca w
którym wchodzi druga krawędź ścieżki (Rys. 5).
Ponadto każda ścieżka powiększająca w
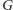 musi być takiej postaci
(tzn. jeśli przecina kielich, to wchodzi do niego krawędzią łodygi), zatem jest
również ścieżką powiększającą w
musi być takiej postaci
(tzn. jeśli przecina kielich, to wchodzi do niego krawędzią łodygi), zatem jest
również ścieżką powiększającą w
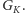
Jako zadanie dla Czytelnika pozostawiamy wykazanie, że jeśli w
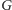 istnieje
ścieżka powiększająca, to nasz algorytm wyszukujący ścieżki powiększające
albo ją znajdzie, albo znajdzie kielich, który można ściągnąć.
istnieje
ścieżka powiększająca, to nasz algorytm wyszukujący ścieżki powiększające
albo ją znajdzie, albo znajdzie kielich, który można ściągnąć.
Znalezienie ścieżki powiększającej z ustalonego wierzchołka zajmuje czas
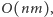 gdyż potencjalnie aż
gdyż potencjalnie aż
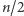 razy będziemy musieli
wykonać ściągnięcie kielicha. Zatem cały algorytm działa w czasie
razy będziemy musieli
wykonać ściągnięcie kielicha. Zatem cały algorytm działa w czasie
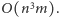
Na koniec zaznaczmy, że opisane algorytmy nie są najlepszymi znanymi
algorytmami znajdującymi najliczniejsze skojarzenia w grafach, są za to
niezbyt skomplikowane. Przykładowo algorytm Hopcrofta–Karpa dla
grafów dwudzielnych oraz algorytm Micalego–Vaziraniego dla grafów
dowolnych działają w czasie
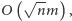 zaś randomizowany algorytm
Muchy–Sankowskiego sprowadza znajdowanie skojarzenia w grafie dowolnym
do problemu mnożenia macierzy i działa w czasie
zaś randomizowany algorytm
Muchy–Sankowskiego sprowadza znajdowanie skojarzenia w grafie dowolnym
do problemu mnożenia macierzy i działa w czasie
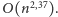
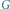 z wyróżnionymi krawędziami odwiedzonymi podczas
przeszukiwania w głąb oraz graf skierowany
z wyróżnionymi krawędziami odwiedzonymi podczas
przeszukiwania w głąb oraz graf skierowany
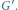 W obu grafach podpisano wierzchołki ze
zbioru
W obu grafach podpisano wierzchołki ze
zbioru
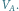
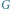 z zaznaczonym kielichem. Na górze po prawej: graf
z zaznaczonym kielichem. Na górze po prawej: graf
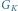 z zaznaczoną ścieżką powiększającą. Na dole: dwie możliwości uzupełnienia
ścieżki powiększającej w grafie
z zaznaczoną ścieżką powiększającą. Na dole: dwie możliwości uzupełnienia
ścieżki powiększającej w grafie