Informatyczny kącik olimpijski
Dwóch generałów
W tym kąciku zajmiemy się zadaniem Dwóch generałów, które pochodzi z Uniwersyteckich Zawodów Informatycznych organizowanych przez Uniwersytet Jagielloński, a konkretnie z konkursu z października 2009 roku.
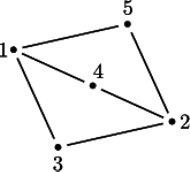
Rys. 1 Dla powyższego planu Bitlandii, jeśli armia zaczyna w mieście 1, to generał A może
przesunąć ją do miasta 3, 4 lub 5. Niezależnie od jego wyboru generałowi B pozostaje
jedyny ruch do miasta 2. Generał A rusza wtedy do jeszcze nieodwiedzonego miasta ze
zbioru
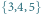 i wygrywa. Jeśli armia zaczyna w mieście 3, to wygra generał B.
i wygrywa. Jeśli armia zaczyna w mieście 3, to wygra generał B.
Zadanie. Generałowie A i B rywalizują ze sobą, na przemian dyktując
ruchy bajtockiej armii, która prowadzi kampanię wojenną w Bitlandii.
W kraju tym jest
 miast połączonych między sobą dwukierunkowymi
drogami. Ruch armii polega na przesunięciu jej z miasta, w którym
stacjonuje, wzdłuż drogi, do jednego z miast sąsiednich. Każde miasto,
w którym znajdzie się armia, zostaje złupione i spalone – nie można
go więc odwiedzić ponownie. Jeśli generał nie będzie mógł wykonać
ruchu, to ośmieszy się przed armią i przegra rywalizację. Dla każdej
początkowej pozycji armii należy rozstrzygnąć, który z generałów wygra,
zakładając, że generał A zaczyna i że obaj generałowie grają optymalnie
(patrz Rys. 1).
miast połączonych między sobą dwukierunkowymi
drogami. Ruch armii polega na przesunięciu jej z miasta, w którym
stacjonuje, wzdłuż drogi, do jednego z miast sąsiednich. Każde miasto,
w którym znajdzie się armia, zostaje złupione i spalone – nie można
go więc odwiedzić ponownie. Jeśli generał nie będzie mógł wykonać
ruchu, to ośmieszy się przed armią i przegra rywalizację. Dla każdej
początkowej pozycji armii należy rozstrzygnąć, który z generałów wygra,
zakładając, że generał A zaczyna i że obaj generałowie grają optymalnie
(patrz Rys. 1).
Plan Bitlandii możemy traktować jako graf nieskierowany
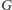 o
o
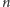 wierzchołkach i
wierzchołkach i
 krawędziach. Na początek
spróbujmy rozwiązać prostszą wersję tego zadania, w której graf
krawędziach. Na początek
spróbujmy rozwiązać prostszą wersję tego zadania, w której graf
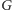 jest dwudzielny (wierzchołki reprezentujące miasta możemy
podzielić na dwa zbiory
jest dwudzielny (wierzchołki reprezentujące miasta możemy
podzielić na dwa zbiory
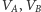 tak, że każda krawędź-droga
łączy wierzchołki znajdujące się w różnych zbiorach). Niech miasto
początkowe będzie w
tak, że każda krawędź-droga
łączy wierzchołki znajdujące się w różnych zbiorach). Niech miasto
początkowe będzie w
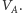 W tej sytuacji ruch generała A zawsze
prowadzi z
W tej sytuacji ruch generała A zawsze
prowadzi z
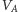 do
do
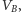 zaś ruch generała B – przeciwnie.
Rozważmy pewną rozgrywkę między generałami, w której zwycięża generał
A oraz wszystkie miasta Bitlandii zostały odwiedzone. W rozgrywce
tej dla każdego miasta
zaś ruch generała B – przeciwnie.
Rozważmy pewną rozgrywkę między generałami, w której zwycięża generał
A oraz wszystkie miasta Bitlandii zostały odwiedzone. W rozgrywce
tej dla każdego miasta
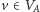 generał A wybrał pewne miasto
generał A wybrał pewne miasto
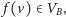 do którego ruszył się z
do którego ruszył się z
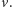 Z warunków zadania
wynika, że funkcja
Z warunków zadania
wynika, że funkcja
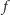 jest bijekcją. Ponadto, zbiór krawędzi,
którymi poruszał się generał A, jest doskonałym skojarzeniem w grafie
jest bijekcją. Ponadto, zbiór krawędzi,
którymi poruszał się generał A, jest doskonałym skojarzeniem w grafie
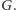
Zauważmy więc, że jeśli w grafie
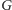 istnieje doskonałe skojarzenie
istnieje doskonałe skojarzenie
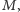 to generał A wygrywa, startując z dowolnego miasta, a jego strategia
polega na poruszaniu się po krawędziach ze skojarzenia
to generał A wygrywa, startując z dowolnego miasta, a jego strategia
polega na poruszaniu się po krawędziach ze skojarzenia
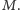 Generał B
nigdy nie będzie mógł zrobić ruchu krawędzią z
Generał B
nigdy nie będzie mógł zrobić ruchu krawędzią z
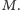
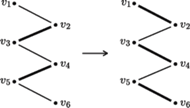
Rys. 2 Ilustracja przypadku dla
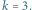 Krawędzie należące do
Krawędzie należące do
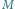 są pogrubione.
są pogrubione.
No dobrze, ale co w przypadku, gdy w
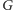 nie istnieje doskonałe
skojarzenie? Niech
nie istnieje doskonałe
skojarzenie? Niech
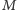 będzie pewnym najliczniejszym skojarzeniem
w
będzie pewnym najliczniejszym skojarzeniem
w
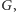 zaś
zaś
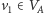 będzie wierzchołkiem początkowym,
który nie jest skojarzony w
będzie wierzchołkiem początkowym,
który nie jest skojarzony w
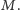 Zauważmy, że jakikolwiek
ruch generała A musi prowadzić do wierzchołka
Zauważmy, że jakikolwiek
ruch generała A musi prowadzić do wierzchołka
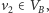 który
jest skojarzony w
który
jest skojarzony w
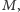 inaczej bowiem moglibyśmy powiększyć
inaczej bowiem moglibyśmy powiększyć
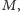 dokładając do niego krawędź
dokładając do niego krawędź
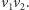 Generał B może
wtedy odpowiedzieć ruchem wzdłuż krawędzi z
Generał B może
wtedy odpowiedzieć ruchem wzdłuż krawędzi z
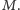 Okazuje
się, że będzie mógł tak zrobić zawsze. Załóżmy bowiem, że
w
Okazuje
się, że będzie mógł tak zrobić zawsze. Załóżmy bowiem, że
w
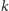 -tym ruchu generał B trafia na nieskojarzony wierzchołek,
czyli
-tym ruchu generał B trafia na nieskojarzony wierzchołek,
czyli
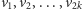 jest ciągiem odwiedzonych wierzchołków,
jest ciągiem odwiedzonych wierzchołków,
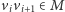 wtedy gdy
wtedy gdy
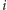 jest parzyste, oraz
jest parzyste, oraz
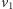 i
i
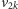 są
nieskojarzone w
są
nieskojarzone w
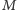 (Rys. 2). Wówczas możemy usunąć ze skojarzenia
(Rys. 2). Wówczas możemy usunąć ze skojarzenia
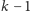 krawędzi
krawędzi
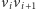 dla
dla
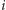 parzystego, a zamiast tego
dołożyć
parzystego, a zamiast tego
dołożyć
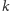 krawędzi
krawędzi
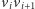 dla
dla
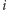 nieparzystego, co daje
skojarzenie liczniejsze niż
nieparzystego, co daje
skojarzenie liczniejsze niż
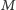 – sprzeczność. Wynika z tego, że jeśli
w grafie
– sprzeczność. Wynika z tego, że jeśli
w grafie
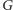 pewne najliczniejsze skojarzenie nie kojarzy wierzchołka
początkowego, to skojarzenie to wyznacza strategię wygrywającą dla generała
B.
pewne najliczniejsze skojarzenie nie kojarzy wierzchołka
początkowego, to skojarzenie to wyznacza strategię wygrywającą dla generała
B.
Pozostał do rozważenia przypadek, w którym wierzchołek początkowy
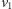 jest skojarzony w każdym najliczniejszym skojarzeniu. Niech
jest skojarzony w każdym najliczniejszym skojarzeniu. Niech
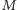 będzie pewnym takim skojarzeniem. Pokażemy, że wygrywa
generał A, a jego strategią jest poruszanie się wzdłuż krawędzi skojarzenia
będzie pewnym takim skojarzeniem. Pokażemy, że wygrywa
generał A, a jego strategią jest poruszanie się wzdłuż krawędzi skojarzenia
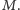 Argument jest podobny jak poprzednio: gdyby w pewnym momencie
dla ciągu odwiedzonych wierzchołków
Argument jest podobny jak poprzednio: gdyby w pewnym momencie
dla ciągu odwiedzonych wierzchołków
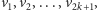 wierzchołek
wierzchołek
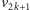 był nieskojarzony w
był nieskojarzony w
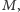 to wymieniając
to wymieniając
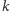 krawędzi
krawędzi
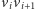 dla
dla
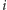 nieparzystego na
nieparzystego na
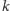 krawędzi
krawędzi
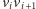 dla
dla
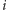 parzystego, dostajemy nowe skojarzenie (równoliczne z
parzystego, dostajemy nowe skojarzenie (równoliczne z
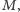 a więc
o największej liczności), które nie kojarzy wierzchołka
a więc
o największej liczności), które nie kojarzy wierzchołka
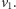 Znów
dochodzimy do sprzeczności.
Znów
dochodzimy do sprzeczności.
Wystarczy zatem dla każdego wierzchołka
 sprawdzić, czy
każde najliczniejsze skojarzenie kojarzy ten wierzchołek. Dowolne
najliczniejsze skojarzenie
sprawdzić, czy
każde najliczniejsze skojarzenie kojarzy ten wierzchołek. Dowolne
najliczniejsze skojarzenie
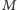 możemy wyznaczyć np. w czasie
możemy wyznaczyć np. w czasie
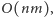 poprzez
poprzez
 -krotne wyszukanie ścieżki powiększającej.
Wierzchołek
-krotne wyszukanie ścieżki powiększającej.
Wierzchołek
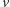 jest kojarzony w każdym najliczniejszym skojarzeniu,
jeśli jest skojarzony w
jest kojarzony w każdym najliczniejszym skojarzeniu,
jeśli jest skojarzony w
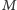 oraz, po usunięciu
oraz, po usunięciu
 z grafu,
liczność najliczniejszego skojarzenia się zmniejsza. Zauważmy, że
szukając skojarzenia, nie musimy zaczynać zawsze od nowa, wystarczy
w skojarzeniu
z grafu,
liczność najliczniejszego skojarzenia się zmniejsza. Zauważmy, że
szukając skojarzenia, nie musimy zaczynać zawsze od nowa, wystarczy
w skojarzeniu
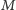 usunąć krawędź kojarzącą
usunąć krawędź kojarzącą
 oraz poszukać
jednej ścieżki powiększającej. Zatem cały algorytm działa w czasie
oraz poszukać
jednej ścieżki powiększającej. Zatem cały algorytm działa w czasie
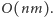
W tym momencie Czytelnik może pokręcić z powątpiewaniem głową, że,
owszem, zrobiliśmy rozgrzewkę i rozwiązaliśmy zadanie dla grafów
dwudzielnych – ale jak nasze rozważania mają się do rozwiązania dla grafów
dowolnych? I będzie miał słuszność, gdyż w istocie wiele problemów,
które umiemy sprawnie rozwiązać dla grafów dwudzielnych, staje się trudne
dla grafów niemających tej własności. Zachęcam jednak Czytelnika do
przeczytania jeszcze raz powyższego rozwiązania i przekonania się, że tak
naprawdę nigdzie nie korzystamy z założenia, że graf
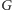 jest
dwudzielny. Zatem nasze rozwiązanie działa również w ogólnym przypadku,
pod warunkiem że umiemy znajdować najliczniejsze skojarzenia w dowolnych
grafach. Można to zrobić w czasie
jest
dwudzielny. Zatem nasze rozwiązanie działa również w ogólnym przypadku,
pod warunkiem że umiemy znajdować najliczniejsze skojarzenia w dowolnych
grafach. Można to zrobić w czasie
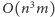 algorytmem Edmondsa
i w takim też czasie działa całe rozwiązanie.
algorytmem Edmondsa
i w takim też czasie działa całe rozwiązanie.
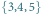 i wygrywa. Jeśli armia zaczyna w mieście 3, to wygra generał B.
i wygrywa. Jeśli armia zaczyna w mieście 3, to wygra generał B.
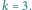 Krawędzie należące do
Krawędzie należące do
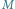 są pogrubione.
są pogrubione.
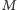 (tzn. każdy wierzchołek jest skojarzony w
(tzn. każdy wierzchołek jest skojarzony w
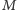 ).
).