Informatyczny kącik olimpijski
Opóźnione wyszukiwanie
W tym kąciku zajmiemy się zadaniem Delayed search, które pojawiło się w 2004 r. w konkursie Internet Problem Solving Contest, organizowanym co roku przez Słowaków. Zadanie jest wariacją na temat znanej zabawy „zgadnij, o jakiej liczbie myślę”...

Organizatorzy wybrali pewną liczbę naturalną
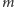 z przedziału
z przedziału
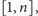 a my mamy ją wyznaczyć, zadając pytania „jak się ma wybrana
liczba do liczby
a my mamy ją wyznaczyć, zadając pytania „jak się ma wybrana
liczba do liczby
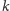 ”, na które dostajemy odpowiedź, że jest ona mniejsza,
większa lub równa
”, na które dostajemy odpowiedź, że jest ona mniejsza,
większa lub równa
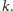 Zadanie ma jednak dodatkowe urozmaicenie:
odpowiedź na
Zadanie ma jednak dodatkowe urozmaicenie:
odpowiedź na
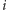 -te pytanie dostajemy dopiero po zadaniu pytania
numer
-te pytanie dostajemy dopiero po zadaniu pytania
numer
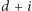 (w szczególności, pierwszą odpowiedź po zadaniu
(w szczególności, pierwszą odpowiedź po zadaniu
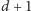 pytań). Ponieważ za każde zadane pytanie naliczane są nam
punkty karne, chcemy znaleźć liczbę
pytań). Ponieważ za każde zadane pytanie naliczane są nam
punkty karne, chcemy znaleźć liczbę
 za pomocą jak najmniejszej
liczby pytań. Zabawa kończy się, gdy usłyszymy odpowiedź „wybrana
liczba jest równa
za pomocą jak najmniejszej
liczby pytań. Zabawa kończy się, gdy usłyszymy odpowiedź „wybrana
liczba jest równa
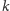 ”. Warto dodać, że chcemy zminimalizować
liczbę pytań zadanych w pesymistycznym przypadku – organizatorzy
nie muszą ustalać
”. Warto dodać, że chcemy zminimalizować
liczbę pytań zadanych w pesymistycznym przypadku – organizatorzy
nie muszą ustalać
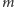 zawczasu, mogą swą decyzję opierać na
naszych pytaniach tak, aby wymusić na nas zadanie jak największej ich
liczby.
zawczasu, mogą swą decyzję opierać na
naszych pytaniach tak, aby wymusić na nas zadanie jak największej ich
liczby.
Dla
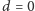 rozwiązanie jest znane: używamy wyszukiwania binarnego.
Każde pytanie dzieli przedział, w którym może znajdować się
rozwiązanie jest znane: używamy wyszukiwania binarnego.
Każde pytanie dzieli przedział, w którym może znajdować się
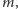 na
pół, potrzebujemy zatem
na
pół, potrzebujemy zatem
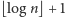 pytań. Pożyteczne będzie
przyjrzenie się tej strategii bliżej. Załóżmy, że mamy ustaloną liczbę pytań,
pytań. Pożyteczne będzie
przyjrzenie się tej strategii bliżej. Załóżmy, że mamy ustaloną liczbę pytań,
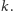 Zastanówmy się, jaka jest największa długość przedziału
Zastanówmy się, jaka jest największa długość przedziału
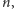 dla
której
dla
której
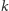 pytań wystarczy do wyznaczenia
pytań wystarczy do wyznaczenia
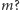 Oznaczmy tę liczbę
przez
Oznaczmy tę liczbę
przez
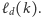
Oczywiście,
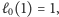 bo musimy zadać jedno pytanie o liczbę 1, by
dostać odpowiedź, że zgadliśmy poprawnie. Załóżmy, że mamy
bo musimy zadać jedno pytanie o liczbę 1, by
dostać odpowiedź, że zgadliśmy poprawnie. Załóżmy, że mamy
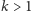 oraz przedział
oraz przedział
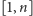 i że zadajemy pierwsze pytanie
o liczbę
i że zadajemy pierwsze pytanie
o liczbę
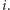 Mamy do rozważenia trzy przypadki: albo mamy
szczęście,
Mamy do rozważenia trzy przypadki: albo mamy
szczęście,
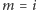 i gra się kończy, albo
i gra się kończy, albo
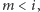 zostaje nam
zostaje nam
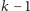 pytań i wiemy, że szukana liczba znajduje się w przedziale
pytań i wiemy, że szukana liczba znajduje się w przedziale
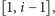 albo
albo
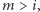 mamy
mamy
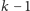 pytań i przedział
pytań i przedział
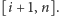 Ponieważ
Ponieważ
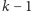 pytań wystarczy dla przedziału
o długości
pytań wystarczy dla przedziału
o długości
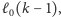 więc zmieścimy się w limicie pytań,
o ile
więc zmieścimy się w limicie pytań,
o ile
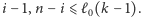 Opłaca nam się, żeby przedziały
Opłaca nam się, żeby przedziały
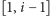 i
i
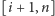 były jak najdłuższe, więc możemy przyjąć
dowolne
były jak najdłuższe, więc możemy przyjąć
dowolne
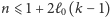 oraz
oraz
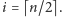 Zatem
Zatem
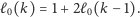 |
Rozwiązując tę rekurencję, dostajemy, że
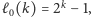 co dla
„klasycznych” 20 pytań daje nam przedział długości
co dla
„klasycznych” 20 pytań daje nam przedział długości
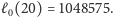
Dla
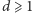 możemy zastosować trywialną strategię: po każdym pytaniu
czekamy na odpowiedź, zadając
możemy zastosować trywialną strategię: po każdym pytaniu
czekamy na odpowiedź, zadając
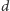 „głupich” pytań. Taka strategia
wymaga zadania
„głupich” pytań. Taka strategia
wymaga zadania
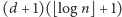 pytań. Nie jest zbyt dobrze, gdyż
w ten sposób 20 pytań pozwoli nam dla
pytań. Nie jest zbyt dobrze, gdyż
w ten sposób 20 pytań pozwoli nam dla
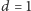 jedynie na przedział
długości
jedynie na przedział
długości
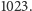 Zdradzimy zaś, że optymalna strategia daje
Zdradzimy zaś, że optymalna strategia daje
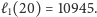 Musimy więc umieć wyznaczać kolejne pytania, zanim
dostaniemy odpowiedź na poprzednie.
Musimy więc umieć wyznaczać kolejne pytania, zanim
dostaniemy odpowiedź na poprzednie.
Rozważmy przypadek
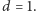 Załóżmy, że pierwsze dwa pytania
są o liczby
Załóżmy, że pierwsze dwa pytania
są o liczby
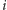 oraz
oraz
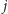 (bez straty ogólności
(bez straty ogólności
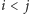 ).
W tym momencie znamy już odpowiedź na pierwsze z tych pytań.
Jeśli więc gra się nie skończyła, to albo
).
W tym momencie znamy już odpowiedź na pierwsze z tych pytań.
Jeśli więc gra się nie skończyła, to albo
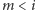 i wtedy pytanie
o
i wtedy pytanie
o
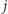 jest stracone (wiemy na pewno, że
jest stracone (wiemy na pewno, że
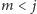 ), zatem mamy
), zatem mamy
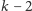 pytań i przedział
pytań i przedział
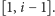 Jeśli zaś
Jeśli zaś
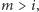 to
zostajemy z przedziałem
to
zostajemy z przedziałem
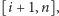 w którym zadaliśmy już jedno
pytanie
w którym zadaliśmy już jedno
pytanie
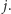 Mogliśmy więc przewidzieć tę sytuację i użyć jako
Mogliśmy więc przewidzieć tę sytuację i użyć jako
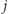 pierwszego pytania z optymalnej strategii dla
pierwszego pytania z optymalnej strategii dla
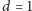 i przedziału
długości
i przedziału
długości
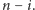 Dzięki temu nie marnujemy tego pytania i w sumie
zostaje nam
Dzięki temu nie marnujemy tego pytania i w sumie
zostaje nam
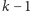 pytań. Stosując rozumowanie jak poprzednio,
mamy
pytań. Stosując rozumowanie jak poprzednio,
mamy
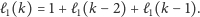 |
Ponieważ
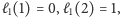 więc rozwiązaniem rekurencji jest
więc rozwiązaniem rekurencji jest
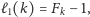 gdzie
gdzie
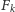 jest
jest
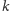 -tą liczbą Fibonacciego. Zatem
strategia postępowania dla
-tą liczbą Fibonacciego. Zatem
strategia postępowania dla
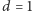 jest następująca: zadajemy pytanie,
dzieląc najdłuższy przedział w złotej proporcji.
jest następująca: zadajemy pytanie,
dzieląc najdłuższy przedział w złotej proporcji.
Podobną strategię możemy zastosować dla
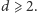 Zadajemy
Zadajemy
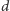 pytań: pierwsze o liczbę
pytań: pierwsze o liczbę
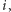 a następne o coraz większe liczby
zgodnie z optymalną strategią dla przedziału długości
a następne o coraz większe liczby
zgodnie z optymalną strategią dla przedziału długości
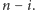 Jeśli gra
się nie skończyła, to albo
Jeśli gra
się nie skończyła, to albo
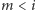 i mamy
i mamy
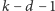 pytań na
przedziale długości
pytań na
przedziale długości
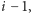 albo
albo
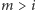 i mamy
i mamy
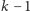 pytań
na pozostałej części przedziału. Zatem
pytań
na pozostałej części przedziału. Zatem
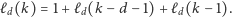 |
Okazuje się, że powyższa strategia jest optymalna. Dowód tego faktu jest
nieco techniczny, zainteresowanych Czytelników odsyłamy do pracy [1]. Jej
autorzy podają również „życiowy” przykład zastosowania „opóźnionego”
wyszukiwania binarnego. Chcieli oni mianowicie wyznaczyć optymalny poziom
trudności prac domowych dla grupy studentów, zadając im prace i analizując
ich wyniki (tzn. sprawdzając, czy sobie z nimi poradzili, czy nie). Z uwagi jednak
na organizację zajęć studenci dostawali nową pracę domową co tydzień,
a mieli ją oddać na następnych zajęciach. Zatem profesorowie musieli
przygotować zadania na zajęcia w tygodniu
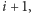 zanim sprawdzili
zadania z tygodnia
zanim sprawdzili
zadania z tygodnia
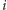 – zastosowali zatem powyższy algorytm dla
– zastosowali zatem powyższy algorytm dla