Bliźniacze programy liniowe

Program liniowy jest to minimalizacja (maksymalizacja) liniowej funkcji celu o   argumentach 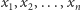 przy zachowaniu pewnej liczby równości lub nierówności liniowych zawierających zmienne 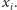 Oto przykład:

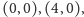
Ponieważ w powyższym przykładzie mamy tylko dwie zmienne, możemy łatwo wyobrazić sobie zbiór rozwiązań dopuszczalnych, tzn. zbiór punktów w przestrzeni dwuwymiarowej spełniających podane nierówności. Jest to czworokąt o wierzchołkach  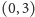i 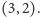  Interesują nas rozwiązania optymalne, czyli rozwiązania dopuszczalne, które minimalizują (maksymalizują) funkcję celu. W szczególności, jeśli zbiór rozwiązań dopuszczalnych jest nieograniczony, rozwiązanie optymalne może nie istnieć. Dla programów o wszystkich zmiennych nieujemnych można dość łatwo wykazać (zachęcam Czytelnika, aby spróbował swoich sił dla dwóch wymiarów), że jeśli jakieś rozwiązanie optymalne istnieje, to istnieje też takie, które jest wierzchołkiem zbioru rozwiązań dopuszczalnych. Po sprawdzeniu wszystkich wierzchołków okazuje się, że rozwiązanie optymalne dla powyższego przykładu to

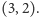
Czy programy liniowe mają coś wspólnego z informatyką? Okazuje się, że bardzo wiele. Po pierwsze, istnieją (bardzo ciekawe!) efektywne algorytmy rozwiązujące programy liniowe. Ponadto, programy liniowe są kluczowym narzędziem w optymalizacji kombinatorycznej, algorytmach aproksymacyjnych czy algorytmach online. Dla przykładu, problem maksymalnego przepływu jest szczególnym przypadkiem programu liniowego (dla sieci o   wierzchołkach i   krawędziach taki program ma  zmiennych i 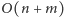  ograniczeń).

Przejdźmy teraz do głównego tematu tego artykułu: każdy program liniowy ma swojego brata bliźniaka. Aby się o tym przekonać, spróbujmy znaleźć jakiś prosty (istotnie prostszy niż dowodzenie twierdzenia o wierzchołkach) sposób, żeby przekonać kolegę, że rozwiązanie 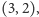 o wartości funkcji celu 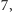 jest faktycznie rozwiązaniem optymalnym, albo chociaż że jest bliskie optymalnemu. Innymi słowy, szukamy oszacowania górnego na wartość funkcji celu rozwiązań dopuszczalnych. Zauważmy, że tak się szczęśliwie złożyło, iż rozwiązania dopuszczalne naszego programu są nieujemne. Dlatego proste oszacowanie możemy dostać już na podstawie pierwszej nierówności: 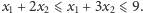 Dodając pierwsze dwie nierówności pomnożone przez 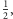 otrzymujemy jeszcze lepsze oszacowanie: 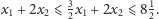 Spróbujmy pójść tą drogą jeszcze dalej. Mianowicie, chcemy znaleźć takie liczby 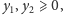 że mnożąc 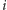-tą nierówność przez 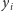 i dodając otrzymane nierówności, dostaniemy jak najlepsze oszacowanie na wartość funkcji celu. Żeby wartość funkcji celu faktycznie szacowała się z góry przez taką sumę, musi zachodzić 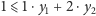 oraz 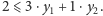 A więc otrzymaliśmy pewne zadanie do rozwiązania. Spostrzegawczy Czytelnik zapewne zauważył już, że jest to zadanie programowania liniowego! Możemy je zapisać następująco:

Ponownie stosując trik z wyznaczeniem wierzchołków wielokąta, otrzymujemy, że 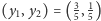 jest rozwiązaniem optymalnym naszego nowego programu. A jaką otrzymaliśmy wartość funkcji celu? Mamy 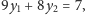 czyli idealnie! Możemy więc łatwo przekonać kolegę, że rozwiązanie 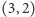 oryginalnego problemu jest nie tylko bliskie optymalnemu, ale nawet że jest optymalne.

Pełna treść artykułu dostępna jest w wersji do druku