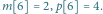Informatyczny kącik olimpijski
Plecak
Jednym z klasycznych problemów algorytmicznych jest tzw. problem plecakowy...

Mamy
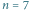 przedmiotów i plecak o udźwigu
przedmiotów i plecak o udźwigu
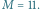 W powyższym drzewie
masa przedmiotu oznaczona jest liczbą kwadracików pod numerem przedmiotu, np.
W powyższym drzewie
masa przedmiotu oznaczona jest liczbą kwadracików pod numerem przedmiotu, np.
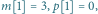 zaś
zaś
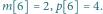
Przedstawiany jest on m.in. w następującej wersji:
Problem. Mamy
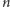 przedmiotów, ponumerowanych liczbami od
przedmiotów, ponumerowanych liczbami od
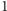 do
do
 Każdy przedmiot ma określoną masę –
Każdy przedmiot ma określoną masę –
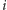 -ty
przedmiot waży
-ty
przedmiot waży
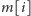 kilogramów. Mamy do dyspozycji plecak, do
którego możemy zapakować przedmioty o łącznej masie co najwyżej
kilogramów. Mamy do dyspozycji plecak, do
którego możemy zapakować przedmioty o łącznej masie co najwyżej
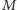 kilogramów. Chcemy dowiedzieć się, jaka jest największa
masa przedmiotów, które możemy zapakować do plecaka, tak by nie
przekroczyć jego udźwigu.
kilogramów. Chcemy dowiedzieć się, jaka jest największa
masa przedmiotów, które możemy zapakować do plecaka, tak by nie
przekroczyć jego udźwigu.
Rozwiązanie tego problemu korzysta z metody programowania
dynamicznego. Mamy tablicę
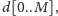 na początku zainicjowaną
wartościami
na początku zainicjowaną
wartościami
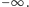 Kolejne przedmioty rozpatrujemy w kolejnych fazach
algorytmu. Będziemy utrzymywali niezmiennik, że po
Kolejne przedmioty rozpatrujemy w kolejnych fazach
algorytmu. Będziemy utrzymywali niezmiennik, że po
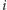 -tej fazie
algorytmu
-tej fazie
algorytmu
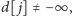 jeśli spośród przedmiotów ze zbioru
jeśli spośród przedmiotów ze zbioru
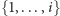 możemy wybrać podzbiór
możemy wybrać podzbiór
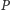 o łącznej masie
o łącznej masie
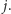 Ponadto
Ponadto
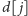 będzie największym numerem przedmiotu, który
można umieścić w pewnym
będzie największym numerem przedmiotu, który
można umieścić w pewnym
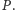

Odpowiedzią jest, oczywiście, największe
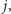 takie że
takie że
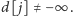 Nasze
rozwiązanie działa w czasie
Nasze
rozwiązanie działa w czasie
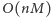 i pamięci
i pamięci
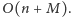
W praktyce jednak, wybierając się na wycieczkę, pakujemy do plecaka rzeczy,
biorąc pod uwagę ich przydatność, a nie tylko to, jak imponująco będzie
wyglądał nasz plecak. W szczególności niektóre z przedmiotów są
bezużyteczne, jeśli w plecaku nie znajdą się z innymi, np. wzięcie
na wakacje statywu nie jest zbyt mądre, jeśli nie weźmiemy aparatu
fotograficznego. I właśnie z tą ciut praktyczniejszą wersją problemu
plecakowego musieli zmierzyć się uczestnicy finału Potyczek Algorytmicznych
2012. Dla każdego przedmiotu
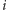 został określony inny przedmiot
został określony inny przedmiot
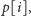 bez którego przedmiot
bez którego przedmiot
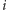 będzie bezużyteczny (albo
będzie bezużyteczny (albo
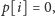 jeśli
jeśli
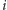 jest przedmiotem przydatnym samym
w sobie). Pytamy znów, jak ciężki plecak możemy zapakować, nie
przekraczając jego udźwigu i nie zabierając żadnego bezużytecznego
przedmiotu.
jest przedmiotem przydatnym samym
w sobie). Pytamy znów, jak ciężki plecak możemy zapakować, nie
przekraczając jego udźwigu i nie zabierając żadnego bezużytecznego
przedmiotu.
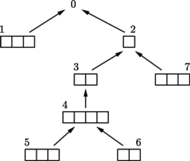
Zależności między przedmiotami możemy przedstawić jako drzewo: dla
każdego przedmiotu
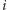 tworzymy krawędź skierowaną z węzła
tworzymy krawędź skierowaną z węzła
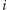 do węzła
do węzła
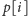 (patrz rysunek). Dodajemy także sztuczny
przedmiot numer
(patrz rysunek). Dodajemy także sztuczny
przedmiot numer
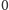 o wadze
o wadze
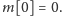 Widzimy, że aby
można było zapakować do plecaka przedmiot
Widzimy, że aby
można było zapakować do plecaka przedmiot
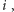 muszą tam
znaleźć się wszystkie przedmioty na ścieżce od węzła
muszą tam
znaleźć się wszystkie przedmioty na ścieżce od węzła
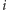 w górę
drzewa.
w górę
drzewa.
Okazuje się, że problem można rozwiązać całkiem prosto, ale wymaga to
pewnej dozy pomysłowości i na zawodach udało się to tylko dwóm
z 20 zawodników. Będziemy przeglądać przedmioty w kolejności
występowania ich w drzewie w porządku preorder (czyli w kolejności
przechodzenia drzewa w głąb – dla ułatwienia przenumerujmy te przedmioty,
jeśli ich kolejność jest inna). Rozważamy przedmiot
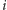 i pytamy się
o warunek istnienia upakowania
i pytamy się
o warunek istnienia upakowania
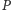 o masie
o masie
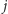 przedmiotami ze
zbioru
przedmiotami ze
zbioru
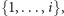 jeśli bierzemy przedmiot
jeśli bierzemy przedmiot
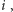 ale nie bierzemy
żadnego bezużytecznego przedmiotu. Załóżmy, że istnieje poprawne
upakowanie plecaka przedmiotami
ale nie bierzemy
żadnego bezużytecznego przedmiotu. Załóżmy, że istnieje poprawne
upakowanie plecaka przedmiotami
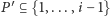 o masie
o masie
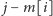 i że
i że
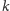 jest największym możliwym numerem
przedmiotu w
jest największym możliwym numerem
przedmiotu w
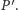 Zauważmy, że jeśli
Zauważmy, że jeśli
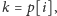 to w oczywisty
sposób
to w oczywisty
sposób
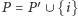 jest poprawnym upakowaniem. Podobnie jeśli
jest poprawnym upakowaniem. Podobnie jeśli
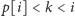 (czyli węzeł
(czyli węzeł
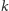 znajduje się w poddrzewie zaczepionym
w lewym bracie węzła
znajduje się w poddrzewie zaczepionym
w lewym bracie węzła
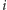 ), to ponieważ
), to ponieważ
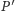 zawiera wszystkie
przedmioty na ścieżce od
zawiera wszystkie
przedmioty na ścieżce od
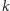 do korzenia, więc zawiera również
przedmiot
do korzenia, więc zawiera również
przedmiot
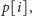 zatem znowu bierzemy
zatem znowu bierzemy
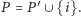 Jeśli
natomiast
Jeśli
natomiast
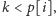 to oznacza, że żadne upakowanie o masie
to oznacza, że żadne upakowanie o masie
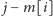 nie może zawierać przedmiotu
nie może zawierać przedmiotu
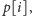 czyli upakowanie
czyli upakowanie
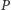 nie może istnieć.
nie może istnieć.
Zaimplementowanie nowego rozwiązania wymaga jedynie kosmetycznej zmiany w poprzednim programie:

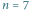 przedmiotów i plecak o udźwigu
przedmiotów i plecak o udźwigu
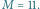 W powyższym drzewie
masa przedmiotu oznaczona jest liczbą kwadracików pod numerem przedmiotu, np.
W powyższym drzewie
masa przedmiotu oznaczona jest liczbą kwadracików pod numerem przedmiotu, np.
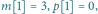 zaś
zaś