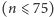W zadaniu dany jest graf skierowany o   wierzchołkach , w którym każda nieuporządkowana para wierzchołków  i 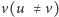  jest połączona dokładnie jedną krawędzią skierowaną (taki graf nazywa się turniejem). Możemy wykonywać operacje kliknięcia w wierzchołek, co powoduje zaznaczenie tego wierzchołka oraz wszystkich wierzchołków, do których wchodzi z niego bezpośrednia krawędź. Naszym celem jest zaznaczenie wszystkich wierzchołków grafu, chcemy przy tym zminimalizować liczbę kliknięć. Należy podać tę liczbę oraz dowolny podzbiór wierzchołków, które należy kliknąć, aby uzyskać ów wynik. Wierzchołki mogą być zaznaczane wielokrotnie.

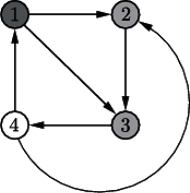
Rysunek obok przedstawia przykładowy turniej dla 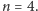 Kliknięcie w wierzchołek numer 1 powoduje zaznaczenie wierzchołków 1, 2 oraz 3.

Dosyć intrygujące w tym zadaniu wydaje się choćby ograniczenie na rozmiar danych wejściowych. Maksymalny rozmiar grafu 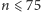 wskazuje raczej na algorytm wielomianowy. Rzadko kiedy mamy jednak do czynienia z algorytmami o złożoności 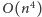 czy 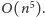 Okazuje się, że w tym zadaniu poszukujemy właśnie takiego algorytmu.

Czasami, aby rozwiązać zadanie dobrze, należy najpierw rozwiązać zadanie źle. Pierwszym pomysłem, który mógłby się nasunąć, byłoby rozwiązanie heurystyczne. Na przykład takie: wybieramy wierzchołek o największym stopniu i klikamy go, następnie wyrzucamy z grafu wszystkie zaznaczone wierzchołki i analogicznie próbujemy zaznaczyć resztę. Rozwiązanie to może nie zadziałać (choćby wtedy, gdy wszystkie wierzchołki mają równy stopień). Narysowanie kontrprzykładu pozostawiam Czytelnikowi (nie jest to, wbrew pozorom, takie łatwe!). Pytanie, jakie należałoby sobie w tym momencie zadać, brzmi:

jaki wynik w najgorszym przypadku zwróci owo błędne rozwiązanie? Odpowiedź może być zaskakująca: zaledwie sześć!

Zauważmy, że każdy wierzchołek jest incydentny z 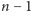  krawędziami. Mogą być one skierowane albo od niego, albo do niego. Nie może być tak, żeby każdy wierzchołek miał większy stopień wejściowy niż wyjściowy, więc w grafie musi istnieć wierzchołek o stopniu wyjściowym co najmniej 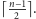 To oznacza, że w pierwszym kroku zaznaczamy co najmniej połowę wierzchołków. Ponadto po usunięciu zaznaczonych wierzchołków oraz krawędzi z nimi incydentnych otrzymujemy nadal turniej, a zatem własność ta zachodzi nie tylko w pierwszym kroku, ale w każdym. Stąd, jeśli 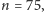 to w kolejnych krokach zostaje nam co najwyżej 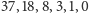 wierzchołków niezaznaczonych. Czyli w najgorszym przypadku wynik dla naszego problemu wynosi sześć, ponadto mamy algorytm, który takie rozwiązanie znajduje.

Wystarczy zatem sprawdzić, czy wynik może być równy pięć lub mniej. Najprostsze naiwne rozwiązanie rozpatruje rzędu 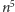 konfiguracji wierzchołków, co dla 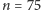 daje ponad 2 miliardy, czyli zdecydowanie za dużo (zwłaszcza że liczba przypadków do rozpatrzenia w jednym pliku testowym wynosiła kilkanaście). Czy naprawdę jest aż tak źle? Okazuje się, że nie. Bardzo łatwo zauważyć, że kolejność klikania wierzchołków jest bez znaczenia. To oznacza, że możemy rozpatrywać każdą nieuporządkowaną piątkę wierzchołków tylko raz (w poprzednim rozwiązaniu każdą taką piątkę analizowalibyśmy 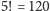 razy), a zatem realnie do przetestowania jest niecałe 20 milionów takich piątek.

Wydawałoby się, że to już koniec. 20 milionów operacji jest wartością akceptowalną. Sęk w tym, że po uwzględnieniu czasu na klikanie i zaznaczanie wierzchołków, a także sprawdzenie, czy wszystkie wierzchołki są już zaznaczone (co z grubsza kosztuje 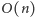), sytuacja wygląda zupełnie inaczej – nadal przekraczamy limit czasu. Czy to oznacza, że należy wykonać jeszcze mniej sprawdzeń? Na szczęście nie, możemy bowiem zredukować czas sprawdzenia.

Zbiór krawędzi wychodzących z każdego wierzchołka można reprezentować w postaci maski bitowej (w tym przypadku można zastosować na przykład trójkę liczb 32-bitowych lub parę liczb 64-bitowych). Dla ułatwienia implementacji możemy dla wierzchołka 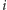 ustawić dodatkową jedynkę na pozycji 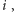 wtedy maska bitowa będzie reprezentować wszystkie wierzchołki, które zostaną zaznaczone po kliknięciu w wierzchołek 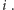 Jeśli chcemy poznać zbiór zaznaczonych wierzchołków, powinniśmy wziąć maski bitowe wszystkich klikniętych wierzchołków i skorzystać z bitowej operacji alternatywy (or). Teraz, aby dowiedzieć się, czy zaznaczyliśmy wszystkie wierzchołki, wystarczy sprawdzić, czy maska bitowa zawiera same jedynki. Zastosowanie masek bitowych pozwala zatem przyspieszyć proces sprawdzania, czy dana piątka wierzchołków jest rozwiązaniem, o czynnik proporcjonalny do liczby bitów dostępnych w wybranym typie całkowitoliczbowym.

Na koniec zauważmy, że oszacowanie liczby konfiguracji przez 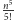 jest bardzo pesymistyczne. W zestawie testów nie znalazł się ani jeden przypadek z wynikiem 6. Pozwala to sądzić, że podany algorytm znajdzie rozwiązanie dużo wcześniej. Wystarczy choćby, żeby kombinacji dających wynik 5 było kilka lub żeby algorytm heurystyczny (podany na początku) dał wynik 5. Proponuję Czytelnikom przygotowanie złośliwych testów do tego zadania, jest to całkiem trudne wyzwanie.