Parzyste, nieparzyste
O zadaniu z Akademickich Mistrzostw Polski w Programowaniu Zespołowym (2012)
Zadanie. Powiemy, że ciąg liczb naturalnych jest
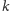 -parzysty, jeśli
każdy jego
-parzysty, jeśli
każdy jego
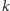 -elementowy spójny fragment ma parzystą sumę.
Przykładowo, ciąg:
-elementowy spójny fragment ma parzystą sumę.
Przykładowo, ciąg:

jest 5-parzysty, a ciąg:

nie. Ile minimalnie wyrazów ciągu
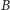 trzeba zmienić, aby stał się on
5-parzysty?
trzeba zmienić, aby stał się on
5-parzysty?

Następujące podejście jest bardzo naturalne. Suma pierwszych pięciu wyrazów
ciągu
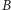 jest równa 16, jest więc parzysta – nic nie trzeba zmieniać. Suma
wyrazów od drugiego do szóstego jest równa 17 – to źle. Aby suma ta stała się
parzysta, wystarczy szósty wyraz ciągu zamienić na jakikolwiek nieparzysty, np.
na 1:
jest równa 16, jest więc parzysta – nic nie trzeba zmieniać. Suma
wyrazów od drugiego do szóstego jest równa 17 – to źle. Aby suma ta stała się
parzysta, wystarczy szósty wyraz ciągu zamienić na jakikolwiek nieparzysty, np.
na 1:

Teraz suma pięciu rozważanych wyrazów jest równa 12 – możemy iść dalej. Kolejny wyraz ciągu jest równy 3, a suma pięciu wyrazów kończących się na tym wyrazie to 13. Wystarczy zatem na siódmej pozycji ciągu wstawić jakąkolwiek liczbę parzystą, np. 2. Nowy ciąg ma postać:

Kontynuując to podejście, zmienimy jeszcze wyrazy 3, 6, 7 i 1. Niestety, wykonaliśmy w sumie sześć zamian, a da się lepiej.
Spróbujmy podejść do zadania bardziej metodycznie. Przede wszystkim
zauważmy, że znaczenie ma jedynie parzystość wyrazów ciągu. Wystarczy
więc, zamiast
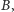 rozważać ciąg:
rozważać ciąg:

Oznaczmy przez
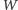 binarny ciąg wynikowy (powstały z
binarny ciąg wynikowy (powstały z
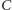 poprzez
minimalną liczbę zamian).
poprzez
minimalną liczbę zamian).
Dla dowolnego
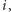 sumy
sumy
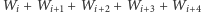 oraz
oraz
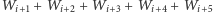 muszą mieć tę samą parzystość. Stąd
muszą mieć tę samą parzystość. Stąd
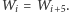 Widzimy zatem, że ciąg
Widzimy zatem, że ciąg
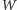 rozpada się na
5 podciągów stałych:
rozpada się na
5 podciągów stałych:
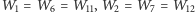 itd.
itd.
Zapiszmy ciąg
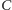 tak, aby wyrazy o indeksach różniących się
o 5 znajdowały się jeden pod drugim:
tak, aby wyrazy o indeksach różniących się
o 5 znajdowały się jeden pod drugim:

 Aby wykonać jak najmniej zamian, w pierwszej
kolumnie ustawimy same zera, w drugiej – same jedynki, w trzeciej – zera,
w czwartej i piątej – jedynki. Razem wyszły nam trzy zamiany. Jakie to
proste!
Aby wykonać jak najmniej zamian, w pierwszej
kolumnie ustawimy same zera, w drugiej – same jedynki, w trzeciej – zera,
w czwartej i piątej – jedynki. Razem wyszły nam trzy zamiany. Jakie to
proste!Otóż... nie do końca. Zapiszmy nasz wynikowy ciąg:

Oto uzyskany przez nas ciąg wynikowy:

oraz ciąg
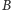 po minimalnej liczbie zamian:
po minimalnej liczbie zamian:
