Informatyczny kącik olimpijski
Czworokąty wypukłe
W tym kąciku zajmiemy się zadaniem Quadrilaterals z obozu w Petrozawodsku
w 2006 roku. Na płaszczyźnie dane jest
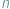 punktów w położeniu
ogólnym (tzn. żadna trójka punktów nie leży na jednej prostej). Należy
wyznaczyć liczbę czworokątów wypukłych, których wierzchołki znajdują się
wśród podanych punktów.
punktów w położeniu
ogólnym (tzn. żadna trójka punktów nie leży na jednej prostej). Należy
wyznaczyć liczbę czworokątów wypukłych, których wierzchołki znajdują się
wśród podanych punktów.
Aby sprawdzić, czy punkty
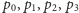 mogą być kolejnymi
wierzchołkami czworokąta wypukłego w porządku przeciwnym do kierunku
ruchu wskazówek zegara, wystarczy zbadać, czy każda trójka kolejnych
punktów tworzy zakręt w lewo. W tym celu można zbadać znak iloczynu
wektorowego:
mogą być kolejnymi
wierzchołkami czworokąta wypukłego w porządku przeciwnym do kierunku
ruchu wskazówek zegara, wystarczy zbadać, czy każda trójka kolejnych
punktów tworzy zakręt w lewo. W tym celu można zbadać znak iloczynu
wektorowego:
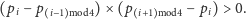
Sprawdzając wszystkie możliwe czwórki uporządkowane, liczbę „dobrych
czwórek” możemy wyznaczyć w czasie
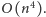 Liczbę czworokątów
wypukłych uzyskamy, dzieląc liczbę „dobrych czwórek” przez 4 (bierzemy
poprawkę na obroty cykliczne).
Liczbę czworokątów
wypukłych uzyskamy, dzieląc liczbę „dobrych czwórek” przez 4 (bierzemy
poprawkę na obroty cykliczne).
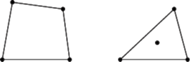
Rys. 1 Dwa przypadki położenia nieuporządkowanej czwórki punktów: A (po lewej) i B (po prawej).
Aby otrzymać szybsze rozwiązanie, skorzystamy z pewnego pomysłowego triku. Rozważmy dowolną nieuporządkowaną czwórkę punktów (w położeniu ogólnym) i zastanówmy się, jakie czworokąty można na niej zbudować. W zależności od wzajemnego ustawienia punktów mamy dwa przypadki (patrz Rys. 1): albo wszystkie punkty leżą na brzegu otoczki wypukłej (przypadek A), albo trzy punkty leżą na brzegu otoczki wypukłej, a czwarty punkt w środku (przypadek B). Łatwo przekonać się, że w pierwszym przypadku czwórka punktów wyznacza jeden czworokąt wypukły, natomiast w drugim przypadku dostajemy trzy różne czworokąty wklęsłe.
Powiemy, że para punktów
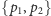 tworzy przecięcie z parą punktów
tworzy przecięcie z parą punktów
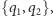 jeśli punkty
jeśli punkty
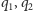 leżą po różnych stronach
prostej wyznaczonej przez punkty
leżą po różnych stronach
prostej wyznaczonej przez punkty
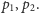 Zauważmy, że czwórka
punktów z przypadku A generuje nam dwa przecięcia (gdy za punkty
Zauważmy, że czwórka
punktów z przypadku A generuje nam dwa przecięcia (gdy za punkty
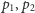 weźmiemy przeciwległe wierzchołki czworokąta wypukłego),
natomiast w przypadku B są to trzy przecięcia (gdy jeden z punktów
weźmiemy przeciwległe wierzchołki czworokąta wypukłego),
natomiast w przypadku B są to trzy przecięcia (gdy jeden z punktów
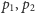 leży w środku otoczki wypukłej). Niech
leży w środku otoczki wypukłej). Niech
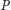 będzie liczbą
wszystkich przecięć w zadanym zbiorze
będzie liczbą
wszystkich przecięć w zadanym zbiorze
 punktów, natomiast
punktów, natomiast
 i
i
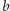 będą liczbą czwórek punktów tworzących układy
odpowiednio typu A i typu B. Możemy napisać następujący układ
równań:
będą liczbą czwórek punktów tworzących układy
odpowiednio typu A i typu B. Możemy napisać następujący układ
równań:

Rozwiązując ten układ, dostajemy, że liczba czworokątów wypukłych
to
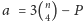 (przy okazji: liczba wszystkich czworokątów to
(przy okazji: liczba wszystkich czworokątów to
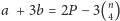 ).
).
Pozostaje pokazać, jak wyznaczyć liczbę
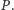 Jeśli dla ustalonej
pary punktów
Jeśli dla ustalonej
pary punktów
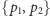 dokładnie
dokładnie
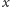 punktów leży po
jednej stronie prostej
punktów leży po
jednej stronie prostej
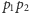 i
i
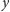 punktów leży po drugiej
stronie tej prostej, to mamy
punktów leży po drugiej
stronie tej prostej, to mamy
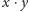 przecięć zawierających parę
przecięć zawierających parę
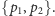 Rozważając każdą taką parę
Rozważając każdą taką parę
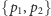 osobno,
uzyskujemy czas
osobno,
uzyskujemy czas
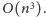
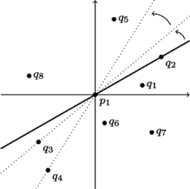
Rys. 2 Przejście prostej ze stanu
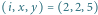 do stanu
do stanu
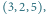 a następnie
do
a następnie
do
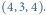
Szybciej wyznaczymy
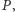 korzystając z metody zamiatania. Ustalmy punkt
korzystając z metody zamiatania. Ustalmy punkt
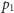 i przesuńmy punkty na płaszczyźnie tak, żeby środek układu
współrzędnych znalazł się w
i przesuńmy punkty na płaszczyźnie tak, żeby środek układu
współrzędnych znalazł się w
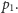 Dla każdego innego punktu
Dla każdego innego punktu
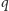 wyznaczmy kąt
wyznaczmy kąt
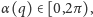 jaki tworzy półprosta
jaki tworzy półprosta
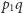 z osią
z osią
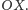 Niech
Niech
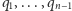 będzie listą tych
punktów posortowaną rosnąco względem kątów
będzie listą tych
punktów posortowaną rosnąco względem kątów
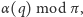 czyli
względem kątów, jakie tworzy prosta
czyli
względem kątów, jakie tworzy prosta
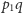 z osią
z osią
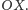 Na początku
przyjmujemy
Na początku
przyjmujemy
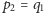 i wyznaczamy liczby
i wyznaczamy liczby
 i
i
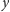 punktów,
które leżą powyżej i poniżej prostej
punktów,
które leżą powyżej i poniżej prostej
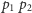 (tj. odpowiednio na
lewo i na prawo od wektora
(tj. odpowiednio na
lewo i na prawo od wektora
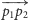 ). W każdym kolejnym kroku
). W każdym kolejnym kroku
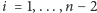 zmieniamy punkt
zmieniamy punkt
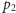 na
na
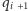 i uaktualniamy
i uaktualniamy
 i
i
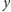 (patrz Rys. 2):
(patrz Rys. 2):

 sortowanie zajmie czas
sortowanie zajmie czas
 a przejrzenie – czas
a przejrzenie – czas
 więc cały algorytm wykona
się w czasie
więc cały algorytm wykona
się w czasie
 Uzyskany wynik (sumę iloczynów
Uzyskany wynik (sumę iloczynów
 )
musimy podzielić przez 2, gdyż interesują nas nieuporządkowane pary
punktów
)
musimy podzielić przez 2, gdyż interesują nas nieuporządkowane pary
punktów

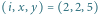 do stanu
do stanu
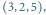 a następnie
do
a następnie
do
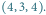
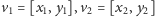 jako liczbę
jako liczbę
