Kliki
Dany jest graf nieskierowany
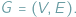 Kliką nazwiemy taki podzbiór
wierzchołków
Kliką nazwiemy taki podzbiór
wierzchołków
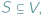 że każde dwa wierzchołki w zbiorze
że każde dwa wierzchołki w zbiorze
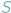 są połączone krawędzią w grafie
są połączone krawędzią w grafie
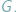 Problem znalezienia
w grafie kliki o jak największej liczbie wierzchołków jest NP-zupełny, a jak
wiadomo, dla takich problemów nikt jeszcze nie pokazał algorytmu
wielomianowego. Podobne trudności są z algorytmem dla problemu zliczania
klik w grafie, choć tutaj stosowną klasę złożoności stanowią tzw. problemy
#P-zupełne.
Problem znalezienia
w grafie kliki o jak największej liczbie wierzchołków jest NP-zupełny, a jak
wiadomo, dla takich problemów nikt jeszcze nie pokazał algorytmu
wielomianowego. Podobne trudności są z algorytmem dla problemu zliczania
klik w grafie, choć tutaj stosowną klasę złożoności stanowią tzw. problemy
#P-zupełne.
Nic więc dziwnego, że gdy takie właśnie zadanie pojawiło się na obozie
w Petrozawodzku w 2009 r. (zadanie pt. Work for Robots), nie oczekiwano od
zawodników rozwiązania wielomianowego. Występujące w zadaniu
ograniczenie
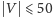 wymagało jednak zastosowania nietrywialnego
algorytmu wykładniczego.
wymagało jednak zastosowania nietrywialnego
algorytmu wykładniczego.
Niech
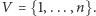 Nasz algorytm będzie wykonywał różne operacje
na podzbiorach zbioru
Nasz algorytm będzie wykonywał różne operacje
na podzbiorach zbioru
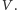 Podzbiory takie będziemy reprezentowali jako
maski bitowe o długości
Podzbiory takie będziemy reprezentowali jako
maski bitowe o długości
 (ponieważ
(ponieważ
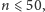 każda taka maska
zmieści się w 64-bitowej zmiennej całkowitej). W pseudokodach będziemy
zapisywać operacje sumy, iloczynu i różnicy zbiorów przy użyciu
standardowej symboliki matematycznej, ale implementując program, można je
równie prosto zapisać przy użyciu operacji bitowych (patrz Delta 11/2008).
Niech
każda taka maska
zmieści się w 64-bitowej zmiennej całkowitej). W pseudokodach będziemy
zapisywać operacje sumy, iloczynu i różnicy zbiorów przy użyciu
standardowej symboliki matematycznej, ale implementując program, można je
równie prosto zapisać przy użyciu operacji bitowych (patrz Delta 11/2008).
Niech
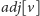 oznacza zbiór wierzchołków, z którymi połączony jest
wierzchołek
oznacza zbiór wierzchołków, z którymi połączony jest
wierzchołek
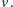 Przez
Przez
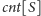 oznaczamy liczbę klik, które są
zawarte w podzbiorze
oznaczamy liczbę klik, które są
zawarte w podzbiorze
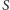 (wynikiem programu będzie
(wynikiem programu będzie
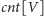 ). Dla
). Dla
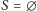 mamy dokładnie jedną taką klikę (pustą). Załóżmy zatem, że
mamy dokładnie jedną taką klikę (pustą). Załóżmy zatem, że
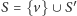 dla pewnego wierzchołka
dla pewnego wierzchołka
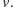 Każda klika zawarta
w
Każda klika zawarta
w
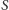 jest albo całkowicie zawarta w
jest albo całkowicie zawarta w
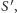 albo zawiera wierzchołek
albo zawiera wierzchołek
 i jest zawarta w
i jest zawarta w
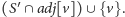
Poniższy pseudokod pokazuje, jak wypełniać tablicę
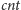 :
:

Powyższe rozwiązanie działa w czasie
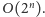
Szybsze rozwiązanie uzyskamy następująco. Podzielmy zbiór wierzchołków na dwa
możliwie równe podzbiory
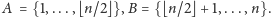 Na
początek wykonajmy powyższy algorytm, ale tylko dla wierzchołków ze zbioru
Na
początek wykonajmy powyższy algorytm, ale tylko dla wierzchołków ze zbioru
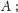 zajmie to czas
zajmie to czas
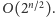 Zbiór
Zbiór
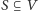 jest kliką
dokładnie wtedy, gdy oba zbiory
jest kliką
dokładnie wtedy, gdy oba zbiory
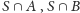 są klikami oraz istnieją
wszystkie krawędzie między nimi. Rozważmy pewien
są klikami oraz istnieją
wszystkie krawędzie między nimi. Rozważmy pewien
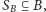 który jest
kliką. Oznaczmy
który jest
kliką. Oznaczmy

czyli zbiór tych wierzchołków, które są połączone ze wszystkimi wierzchołkami
z
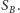 Wówczas klika
Wówczas klika
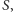 dla której
dla której
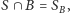 musi
spełniać
musi
spełniać
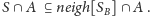 Ostatecznie wynikiem jest:
Ostatecznie wynikiem jest:

przy czym warunek sumy oznacza po prostu, że
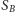 jest kliką.
jest kliką.
To, czego nam teraz potrzeba, to obliczenie
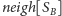 dla wszystkich
dla wszystkich
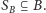 Robimy to podobnie jak w przypadku tablicy
Robimy to podobnie jak w przypadku tablicy
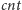 :
:

Całe rozwiązanie działa w czasie
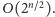 Jako zadanie dla Czytelnika
proponujemy przerobić ten algorytm tak, by znajdował najliczniejszą
klikę.
Jako zadanie dla Czytelnika
proponujemy przerobić ten algorytm tak, by znajdował najliczniejszą
klikę.