Informatyczny kącik olimpijski
Odśnieżanie
Zadanie Odśnieżanie z zeszłorocznego Obozu Naukowo-Treningowego im. A.
Kreczmara można sformułować w języku teorii grafów następująco.
W nieskierowanym, ważonym, spójnym grafie
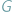 wyróżniono cztery
wierzchołki. Należy usunąć część krawędzi z grafu tak, żeby nadal istniały
ścieżki pomiędzy każdą parą wyróżnionych wierzchołków i żeby suma
wag krawędzi, które pozostały w grafie, była jak najmniejsza.
wyróżniono cztery
wierzchołki. Należy usunąć część krawędzi z grafu tak, żeby nadal istniały
ścieżki pomiędzy każdą parą wyróżnionych wierzchołków i żeby suma
wag krawędzi, które pozostały w grafie, była jak najmniejsza.
Oznaczmy zbiór wierzchołków grafu
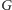 przez
przez
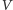 i niech
i niech
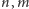 oznaczają liczbę wierzchołków i krawędzi w grafie. Niech
oznaczają liczbę wierzchołków i krawędzi w grafie. Niech
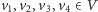 będą wyróżnionymi wierzchołkami. Szukany
optymalny zestaw nieusuniętych krawędzi na pewno nie będzie zawierać cyklu.
Gdyby były tylko dwa wyróżnione wierzchołki,
będą wyróżnionymi wierzchołkami. Szukany
optymalny zestaw nieusuniętych krawędzi na pewno nie będzie zawierać cyklu.
Gdyby były tylko dwa wyróżnione wierzchołki,
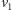 i
i
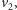 to
nieusunięte krawędzie tworzyłyby najkrótszą ścieżkę z
to
nieusunięte krawędzie tworzyłyby najkrótszą ścieżkę z
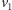 do
do
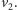 W przypadku trzech wyróżnionych wierzchołków od ścieżki
z
W przypadku trzech wyróżnionych wierzchołków od ścieżki
z
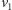 do
do
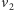 w pewnym miejscu odchodziłaby jeszcze ścieżka do
w pewnym miejscu odchodziłaby jeszcze ścieżka do
 Po chwili namysłu dochodzimy do wniosku, że w przypadku czterech
wyróżnionych wierzchołków nieusunięte krawędzie powinny tworzyć kształt
taki jak na poniższym rysunku. Wyróżnione wierzchołki są tutaj połączone
ścieżkami z pewnymi dwoma wierzchołkami
Po chwili namysłu dochodzimy do wniosku, że w przypadku czterech
wyróżnionych wierzchołków nieusunięte krawędzie powinny tworzyć kształt
taki jak na poniższym rysunku. Wyróżnione wierzchołki są tutaj połączone
ścieżkami z pewnymi dwoma wierzchołkami
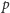 i
i
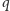 (nazwijmy je
wierzchołkami centralnymi), które również są połączone ścieżką. Bez straty
ogólności wierzchołek
(nazwijmy je
wierzchołkami centralnymi), które również są połączone ścieżką. Bez straty
ogólności wierzchołek
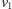 i pewien inny wierzchołek
i pewien inny wierzchołek
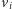 dla
dla
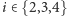 są połączone z
są połączone z
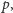 pozostałe dwa są połączone
z
pozostałe dwa są połączone
z
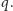 Rysunek obejmuje również przypadki, gdy niektóre wierzchołki
pokrywają się (np.
Rysunek obejmuje również przypadki, gdy niektóre wierzchołki
pokrywają się (np.
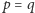 lub
lub
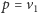 ) – w takich sytuacjach
odpowiednie ścieżki mają zerową długość.
) – w takich sytuacjach
odpowiednie ścieżki mają zerową długość.

Jeśli przez
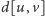 oznaczymy długość najkrótszej ścieżki
pomiędzy wierzchołkami
oznaczymy długość najkrótszej ścieżki
pomiędzy wierzchołkami
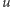 i
i
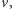 to koszt powyższego rozwiązania
wynosi
to koszt powyższego rozwiązania
wynosi

Parę wierzchołków centralnych
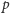 i
i
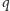 możemy wybrać na
możemy wybrać na
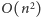 sposobów, zaś wierzchołek
sposobów, zaś wierzchołek
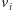 na trzy sposoby. Jednak
złożoność czasowa algorytmu jest zdominowana przez obliczenie tablicy
na trzy sposoby. Jednak
złożoność czasowa algorytmu jest zdominowana przez obliczenie tablicy
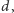 które wykonujemy w czasie
które wykonujemy w czasie
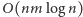 za pomocą
za pomocą
 wywołań algorytmu Dijkstry.
wywołań algorytmu Dijkstry.
Zadanie można rozwiązać szybciej. Ustalmy
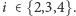 Niech graf
Niech graf
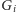 powstaje przez dodanie do grafu
powstaje przez dodanie do grafu
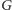 dodatkowych wierzchołków
dodatkowych wierzchołków
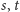 i dodatkowych krawędzi: wierzchołek
i dodatkowych krawędzi: wierzchołek
 łączymy z każdym
wierzchołkiem
łączymy z każdym
wierzchołkiem
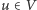 krawędzią o wadze
krawędzią o wadze
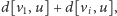 zaś
wierzchołek
zaś
wierzchołek
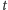 łączymy z każdym
łączymy z każdym
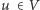 krawędzią o wadze
krawędzią o wadze
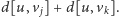
Zauważmy, że ścieżka
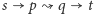 w grafie
w grafie
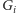 odpowiada
rozwiązaniu, w którym jako wierzchołki centralne wybieramy
odpowiada
rozwiązaniu, w którym jako wierzchołki centralne wybieramy
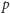 i
i
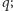 koszt takiego rozwiązania jest równy długości tej
ścieżki. Tak więc, aby rozwiązać zadanie, wystarczy dla każdego
koszt takiego rozwiązania jest równy długości tej
ścieżki. Tak więc, aby rozwiązać zadanie, wystarczy dla każdego
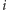 znaleźć najkrótszą ścieżkę z
znaleźć najkrótszą ścieżkę z
 do
do
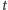 w grafie
w grafie
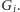
Do konstrukcji grafu
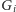 musimy wyznaczyć wartości
musimy wyznaczyć wartości
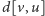 dla
dla
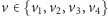 i
i
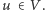 Ostatecznie nasze rozwiązanie wymaga
siedmiu wywołań algorytmu Dijkstry (czterech w grafie
Ostatecznie nasze rozwiązanie wymaga
siedmiu wywołań algorytmu Dijkstry (czterech w grafie
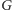 do obliczenia
do obliczenia
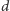 i po jednym w grafie
i po jednym w grafie
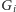 dla każdego wyboru
dla każdego wyboru
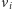 ). Graf
). Graf
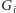 ma
ma
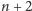 wierzchołków i
wierzchołków i
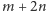 krawędzi, więc koszt
algorytmu Dijkstry jest w nim taki sam jak w grafie
krawędzi, więc koszt
algorytmu Dijkstry jest w nim taki sam jak w grafie
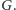 Zatem
rozwiązanie działa w czasie
Zatem
rozwiązanie działa w czasie