Zaczynamy od wypisania kolejno wszystkich liczb od 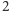 do 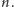 Następnie zaznaczamy 2 i wykreślamy wszystkie jej wielokrotności, zaznaczamy 3 i wykreślamy jej wielokrotności, dalej to samo z kolejnymi niewykreślonymi liczbami: 5, 7 itd. Jest to bardzo efektywna metoda; wykonujemy w niej rzędu 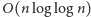 operacji, o czym można przekonać się, czytając artykuł pt. „Jak szybko działa sito?” w Delcie 4/2012. 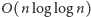 to prawie 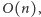 ale jednak nie. Większa niż liniowa złożoność czasowa związana jest z tym, że w sicie Eratostenesa pozwalamy sobie na pewną rozrzutność, gdyż niektóre liczby złożone wykreślamy wielokrotnie. Zależnie od szczegółów implementacyjnych, pierwszą taką liczbą złożoną jest 6 albo 12. Zastanówmy się jednak, czy nie dałoby się każdej liczby złożonej wykreślić dokładnie raz?

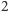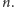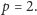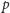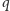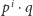Tak jak w zwykłym sicie, na początku tworzymy listę wszystkich liczb od  do  Znów w pierwszym kroku ustalamy liczbę pierwszą  Dalej będzie trochę inaczej niż poprzednio, ale nie tak znowu skomplikowanie. Rozważamy kolejne (niewykreślone i nie mniejsze niż ) liczby  na liście i dla każdej z nich wykreślamy wszystkie liczby postaci  dla

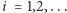
Zobaczmy to na przykładzie; niech

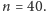
Na początku mamy 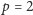 i listę przeglądamy, począwszy od 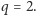 W pierwszym kroku wykreślamy liczby postaci 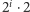 dla 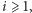 czyli potęgi dwójki:

Przyszła pora na 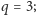 wykreślamy wszystkie liczby postaci :

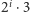Kolejną nieskreśloną liczbą jest 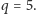 Wykreślamy więc liczby postaci :

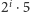Nietrudno zgadnąć, co będzie dalej. Czytelnik zechce sprawdzić, że po pełnym rozpatrzeniu 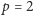 na liście pozostaną po prostu wszystkie liczby nieparzyste.

Przyszła wreszcie pora na 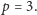 Rozważamy wszystkie dotychczas nieskreślone wartości 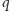 nie mniejsze niż 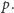 Zaczynamy od 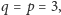 czyli najpierw wykreślamy potęgi trójki:

Następnie mamy 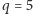 i wykreślamy tylko 15; 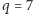 i znika 21; dalej wykreślimy jeszcze 33 i 39:

W ten sposób rozważyliśmy 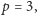 przechodzimy do 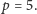 Za pomocą 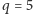 wykreślimy już tylko 25, a za pomocą 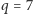 wykreślimy 35.

Dla każdego kolejnego kandydata na 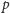 liczba 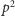 jest większa niż 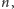 możemy więc śmiało stwierdzić, że na liście pozostały nam już tylko liczby pierwsze (i to wszystkie w badanym zakresie).

W tym przykładzie rzeczywiście każdą liczbę złożoną skreśliliśmy dokładnie raz. Nie jest to przypadek; liczbę złożoną

skreślamy w przebiegu algorytmu, w którym 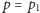 i 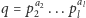 (a jeśli 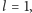 to, oczywiście, dla 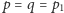). To, w szczególności, oznacza, że dla każdej liczby złożonej obliczamy przy okazji jej najmniejszy dzielnik pierwszy.

Możemy więc pokusić się o stwierdzenie, że cała metoda wykonuje wymarzone 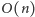 operacji. Aby jednak dało się ją przekuć na algorytm o liniowym koszcie czasowym, musimy przyjrzeć się dokładniej używanej strukturze danych. Mamy tu do czynienia z dwoma typami operacji: znajdowaniem następnego elementu na liście (potrzebne do rozpatrywania kolejnych 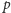 i 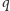 ) oraz wykreśleniem danej liczby z listy. O ile pierwszą z tych operacji wykonuje się na liście standardowo w czasie stałym, o tyle druga z nich sprawia pewien kłopot. W przypadku listy nie mamy bowiem swobodnego dostępu do jej elementów. Taki dostęp daje np. tablica, która to struktura nie pozwala z kolei na proste usuwanie bądź wykreślanie elementów...

Klucz do rozwiązania tej ostatniej trudności stanowi połączenie dwóch wspomnianych struktur danych, czyli listy i tablicy. Dokładniej, oprócz dwukierunkowej listy wszystkich niewykreślonych elementów utrzymujemy tablicę wskaźników do poszczególnych liczb od 2 do  na liście. Jeśli danej liczby nie ma już na liście, w odpowiednim polu tablicy możemy wstawić np. nil. Za pomocą wskaźników zapisanych w tablicy łatwo znajdujemy elementy listy, które chcemy wykreślić, a potem usuwamy je już standardowo – podpinając do siebie wzajemnie następny i poprzedni element listy.

Przykładowo, opisana struktura danych dla 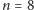 po wykreśleniu potęg dwójki wygląda tak:

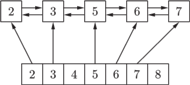
Teraz możemy już z całą pewnością powiedzieć, że otrzymaliśmy liniową metodę wykrywania wszystkich liczb pierwszych w danym początkowym zakresie liczb.

Czy w praktyce jest ona lepsza od klasycznego sita Eratostenesa? Nie sądzę. Za to ma ona pewne ciekawe z teoretycznego punktu widzenia zastosowanie, o czym można przeczytać w kolejnym artykule w tym numerze Delty.