W zadaniu mamy do czynienia z pewnym instrumentem muzycznym, za pomocą którego można zagrać 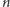 rodzajów nut. Muzyk ma zadaną melodię, którą chciałby zagrać – jest to sekwencja  kolejnych nut. Niestety, nie jest to takie proste. Otóż zagranie każdej nuty wymaga zakrycia niektórych otworów instrumentu, a jeśli dwie nuty istotnie różnią się wymaganym sposobem zakrycia, to muzyk nie jest w stanie zagrać jednej z tych nut bezpośrednio po drugiej... Innymi słowy, dla każdej pary nut wiadomo z góry, czy można zagrać je pod rząd, czy też nie. Z tego względu zagranie zadanej melodii może nie być możliwe. Muzyk chciałby więc zagrać melodię możliwie najbliższą zadanej, to znaczy zagrać taką melodię złożoną z 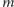  nut, która będzie różniła się od zadanej na najmniejszej możliwej liczbie pozycji – i my mamy mu w tym pomóc. 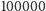Dodajmy, że w naszym zadaniu liczba możliwych nut jest stosunkowo niewielka (rzędu 100), natomiast cała melodia może składać się nawet ze  nut.

Jednym z pierwszych pomysłów, jaki narzuca się po przeczytaniu tego zadania, jest programowanie dynamiczne. Ponumerujmy poszczególne rodzaje nut od 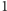 do 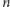 i oznaczmy kolejne nuty w zadanej melodii przez 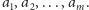 Niech dalej tablica wartości logicznych 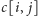 reprezentuje podane pary nut, które można zagrać bezpośrednio jedna po drugiej; zakładamy, że dla każdego 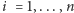 zachodzi 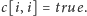 Chcemy wypełnić dwuwymiarową tablic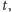ę  w której pole 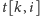 oznacza najmniejszą liczbę błędów, jakie może popełnić muzyk, grając – zamiast fragmentu melodii 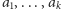– jakąś melodię długości 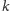 kończącą się nutą typu 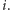 Pomijając warunki brzegowe, pola tablicy 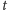 możemy wyznaczać za pomocą prostej zależności rekurencyjnej, w której sprawdzamy wszystkie możliwe rodzaje nut, jakie mogły wystąpić w melodii bezpośrednio przed zadaną nutą:

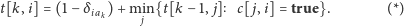W powyższym wzorze 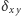 oznacza 1, jeśli 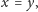 a 0 w przeciwnym przypadku. To rozwiązanie działa w czasie 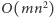 i pamięci

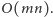
Da się jednak lepiej. Naturalne wydaje się skorzystanie z faktu, że powyższe rozwiązanie oblicza jedynie 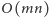 różnych wartości. Gdybyśmy tylko byli w stanie jakoś sprytniej wyznaczać minimum we wzorze 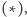 np. w czasie stałym, to uzyskalibyśmy rozwiązanie działające zadowalająco szybko. Pewną wskazówką jest tu pierwszy składnik występujący we wzorze (*). Otóż, w przeciwieństwie do drugiego składnika, może on przyjmować tylko dwie różne wartości, które zależą jedynie od tego, czy w 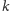  -tym kroku decydujemy się zagrać poprawną nutę 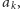 czy też nie.

Przyjrzyjmy się pierwszemu z tych przypadków i spróbujmy zmienić nieco nasze podejście. Gdyby udało nam się wyznaczyć jednowymiarową tablicę 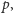 w której 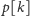 to maksymalna liczba poprawnie zagranych nut podczas wykonywania początkowego fragmentu melodii długości 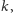 przy założeniu, że 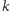 -tą nutę zagramy poprawnie, to moglibyśmy już łatwo podać wynik – byłoby to maksimum ze wszystkich elementów tablicy 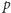 (dlaczego?). 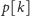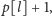Przy wypełnianiu tego typu tablic za pomocą programowania dynamicznego  oblicza się zazwyczaj jako maksimum z tych wartości  dla 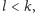 które „pasują do faktu 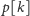 ”. 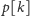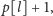W naszym przypadku przy obliczaniu  bierzemy pod uwagę te wartości  dla których istnieje poprawna (czyli możliwa do zagrania) melodia długości 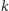 zawierająca na odpowiednich pozycjach nuty 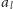 i 

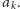
Nie dosyć, że powyższe rozwiązanie ma na starcie złożoność czasową 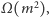 to jeszcze nie bardzo widać, jak takie 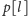 znajdować. Jest do tego potrzebny pewien pomysł: otóż tablicę  możemy potraktować jako macierz sąsiedztwa pewnego grafu. Wówczas wartość 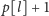 pasuje do 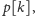 jeśli w tym grafie istnieje ścieżka długości 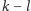 łącząca nuty 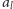 oraz 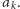 W tym celu wystarczy sprawdzić, czy najkrótsza ścieżka w grafie od 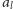 do 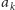 ma długość nieprzekraczającą 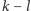 (to przejście myślowe wynika akurat z faktu, że 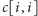 jest zawsze prawdziwe). Najkrótsze ścieżki między wszystkimi parami wierzchołków (nut) możemy wyznaczyć w czasie 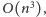 czy to za pomocą algorytmu Floyda–Warshalla, czy to wielokrotnie wykonując przeszukiwanie wszerz.

W ten sposób rozwiązaliśmy problem implementacji nowego rozwiązania, ale ciągle nie uporaliśmy się z jego paskudną złożonością czasową. Jedynym nowym pomysłem, jaki pojawił się po drodze, było wprowadzenie grafu nut. Jeśli zdecydujemy się poświęcić mu jeszcze trochę uwagi, to ta decyzja okaże się kluczowa dla skonstruowania efektywnego rozwiązania.

Potrzebne jest nam mianowicie już tylko następujące spostrzeżenie: graf nut ma zaledwie  wierzchołków, więc wszystkie najkrótsze ścieżki w tym grafie mają długości nieprzekraczające 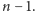 To oznacza, że dla danego 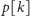 wszystkie wartości 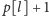 dla 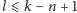 są z pewnością dobre, a zatem przy obliczaniu 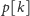 wystarczy tylko rozważyć elementy tablicy położone co najwyżej 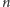 pól wstecz oraz maksimum ze wszystkich elementów położonych jeszcze wcześniej!

Zanim jednak zaczniemy świętować nasz sukces, musimy poczynić przykre spostrzeżenie, że graf nut może nie być spójny. To oznacza, że dla danego 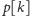 niektóre nawet bardzo odległe wartości 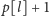 mogą nie być dobre. Przezwyciężenie tej trudności okazuje się już tylko kwestią czasu. Możemy, na przykład, pamiętać zawsze  ostatnich elementów tablicy 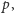 a także maksima ze wszystkich wcześniejszych elementów pogrupowane po poszczególnych nutach (czyli 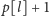 grupujemy po 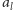 ). Sprytniejsze rozwiązanie polega na rozważeniu każdej spójnej składowej grafu nut z osobna i zastosowaniu dla niej metody z jednym pamiętanym maksimum – wówczas nuty melodii występujące poza składową traktujemy po prostu jako niemożliwe do zagrania. 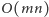W obu przypadkach otrzymujemy algorytm działający w czasie  i pamięci 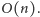 Do tego musimy jeszcze doliczyć koszt wyznaczenia najkrótszych ścieżek: czas 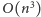 i pamięć

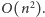
Dodajmy na koniec, że nasz muzyk nie będzie specjalnie zadowolony, jeśli podamy mu jedynie minimalną liczbę błędów, jakie może popełnić – chciałby przecież wiedzieć, jaką melodię powinien zagrać! Polecamy zatem Czytelnikowi zastanowić się nad tym, jak odtworzyć wynik.