Informatyczny kącik olimpijski
Bitoniczny komiwojażer
Tym razem w kąciku lekko zmodyfikowana wersja zadania Listonosz z konkursu Wielka Przesmycka 2004.
W klasycznym problemie komiwojażera mamy dany graf nieskierowany
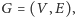 w którym każda krawędź
w którym każda krawędź
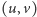 ma przypisaną
pewną nieujemną, całkowitą wagę
ma przypisaną
pewną nieujemną, całkowitą wagę
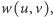 i poszukujemy najlżejszego
cyklu przechodzącego przez każdy wierzchołek grafu dokładnie raz. Ten
problem jest NP-trudny, co znaczy, że nie należy spodziewać się, że uda się
go rozwiązać w czasie wielomianowym (przynajmniej nie w czasie zawodów).
W bitonicznej wersji problemu komiwojażera wprowadzamy jedno dodatkowe
wymaganie dotyczące cyklu. Otóż przyjmujemy, że wierzchołki grafu są
ponumerowane od 1 do
i poszukujemy najlżejszego
cyklu przechodzącego przez każdy wierzchołek grafu dokładnie raz. Ten
problem jest NP-trudny, co znaczy, że nie należy spodziewać się, że uda się
go rozwiązać w czasie wielomianowym (przynajmniej nie w czasie zawodów).
W bitonicznej wersji problemu komiwojażera wprowadzamy jedno dodatkowe
wymaganie dotyczące cyklu. Otóż przyjmujemy, że wierzchołki grafu są
ponumerowane od 1 do
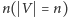 , i poszukujemy najlżejszego cyklu
przechodzącego raz przez każdy wierzchołek grafu, w którym ciąg numerów
wierzchołków jest bitoniczny, czyli najpierw rosnący, a potem malejący
(przy pewnym wyborze wierzchołka startowego cyklu). Jak nietrudno się
domyślić, wymaganie, by cykl był bitoniczny, istotnie upraszcza podany
problem.
, i poszukujemy najlżejszego cyklu
przechodzącego raz przez każdy wierzchołek grafu, w którym ciąg numerów
wierzchołków jest bitoniczny, czyli najpierw rosnący, a potem malejący
(przy pewnym wyborze wierzchołka startowego cyklu). Jak nietrudno się
domyślić, wymaganie, by cykl był bitoniczny, istotnie upraszcza podany
problem.
Nazwijmy interesujące nas w tym zadaniu cykle cyklami bitonicznymi.
Zacznijmy od spostrzeżenia, że wierzchołek numer 1 na pewno znajduje się na
początku bądź na końcu każdego cyklu bitonicznego. W drugim z tych
przypadków możemy przenieść ten wierzchołek na początek cyklu. To
oznacza, że dowolny cykl bitoniczny zaczyna się w wierzchołku 1, prowadzi
pewną ścieżką o rosnących numerach wierzchołków aż do wierzchołka
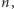 po czym wraca do wierzchołka 1, idąc po malejących numerach
wierzchołków. Na cykl takiej postaci możemy też spojrzeć nieco
inaczej: z wierzchołka 1 prowadzimy dwie rozłączne ścieżki o rosnących
numerach wierzchołków, które na końcu spotykają się w wierzchołku
po czym wraca do wierzchołka 1, idąc po malejących numerach
wierzchołków. Na cykl takiej postaci możemy też spojrzeć nieco
inaczej: z wierzchołka 1 prowadzimy dwie rozłączne ścieżki o rosnących
numerach wierzchołków, które na końcu spotykają się w wierzchołku
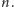 Ścieżki o rosnących numerach wierzchołków będziemy dalej
nazywali po prostu ścieżkami rosnącymi.
Ścieżki o rosnących numerach wierzchołków będziemy dalej
nazywali po prostu ścieżkami rosnącymi.
Takie spojrzenie na nasz problem pozwala uzyskać pierwsze rozwiązanie
wielomianowe. Zastosujemy metodę programowania dynamicznego. Dla każdej
pary wierzchołków
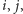 takich że
takich że
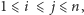 przez
przez
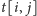 oznaczmy sumę wag w najlżejszej parze ścieżek rosnących
zaczynających się w wierzchołku 1, kończących się odpowiednio w wierzchołkach
oznaczmy sumę wag w najlżejszej parze ścieżek rosnących
zaczynających się w wierzchołku 1, kończących się odpowiednio w wierzchołkach
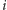 oraz
oraz
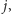 oraz przechodzących przez każdy wierzchołek – poza
wierzchołkiem 1 i, ewentualnie, wierzchołkiem
oraz przechodzących przez każdy wierzchołek – poza
wierzchołkiem 1 i, ewentualnie, wierzchołkiem
 – co najwyżej raz. Po
chwili namysłu zauważamy, że aby dało się te wartości obliczać, na
– co najwyżej raz. Po
chwili namysłu zauważamy, że aby dało się te wartości obliczać, na
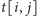 musimy nałożyć jeszcze jeden dodatkowy warunek: nasze dwie
ścieżki rosnące muszą przechodzić przez wszystkie wierzchołki ze zbioru
musimy nałożyć jeszcze jeden dodatkowy warunek: nasze dwie
ścieżki rosnące muszą przechodzić przez wszystkie wierzchołki ze zbioru
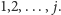 Teraz jest już całkiem prosto opisać przejścia ze stanu
Teraz jest już całkiem prosto opisać przejścia ze stanu
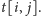 Naszą parę ścieżek rosnących możemy rozszerzyć za pomocą
krawędzi wychodzącej z wierzchołka
Naszą parę ścieżek rosnących możemy rozszerzyć za pomocą
krawędzi wychodzącej z wierzchołka
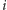 albo z wierzchołka
albo z wierzchołka
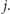 Aby
był spełniony nasz dodatkowy warunek, dodana krawędź musi prowadzić do
wierzchołka
Aby
był spełniony nasz dodatkowy warunek, dodana krawędź musi prowadzić do
wierzchołka
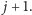 W pierwszym przypadku aktualizujemy wartość
W pierwszym przypadku aktualizujemy wartość
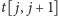 (za pomocą
(za pomocą
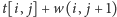 ), a w drugim –
wartość
), a w drugim –
wartość
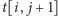 (tym razem za pomocą
(tym razem za pomocą
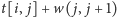 ).
Jeśli jednak
).
Jeśli jednak
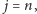 to mamy tylko jedno przejście, do stanu
to mamy tylko jedno przejście, do stanu
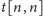 (za pomocą
(za pomocą
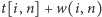 ). Zaczynamy, oczywiście, od
stanu
). Zaczynamy, oczywiście, od
stanu
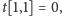 a kończymy w stanie
a kończymy w stanie
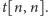 Jeśli graf
będziemy reprezentować za pomocą tablicy sąsiedztwa (czyli funkcję wagi
Jeśli graf
będziemy reprezentować za pomocą tablicy sąsiedztwa (czyli funkcję wagi
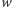 zapiszemy w tablicy dwuwymiarowej), otrzymamy algorytm
o złożoności czasowej
zapiszemy w tablicy dwuwymiarowej), otrzymamy algorytm
o złożoności czasowej
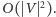
Może wydawać się nieco zaskakujące, że istnieje bardziej efektywne rozwiązanie naszego problemu. Aby je dostrzec, należy przyjrzeć się dokładniej strukturze cyklu bitonicznego.
Załóżmy, że gdzieś na tym cyklu, na jednej ze ścieżek rosnących, leży jakaś
„długa” krawędź
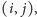 czyli taka, że
czyli taka, że
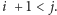 Załóżmy
na razie, że
Załóżmy
na razie, że
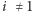 i
i
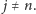 Wówczas możemy od razu
powiedzieć coś o drugiej ścieżce rosnącej: mamy na niej jakąś krawędź
Wówczas możemy od razu
powiedzieć coś o drugiej ścieżce rosnącej: mamy na niej jakąś krawędź
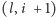 dla
dla
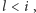 dalej znajduje się sekwencja krawędzi
„jednostkowych”
dalej znajduje się sekwencja krawędzi
„jednostkowych”
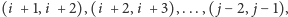 wreszcie
z wierzchołka
wreszcie
z wierzchołka
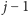 wychodzi krawędź prowadząca do jakiegoś
wierzchołka
wychodzi krawędź prowadząca do jakiegoś
wierzchołka
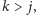 patrz rysunek poniżej.
patrz rysunek poniżej.

Powyższe spostrzeżenie pozwala uprościć postać stanu w naszym
programowaniu dynamicznym. Otóż wystarczy nam tylko jeden parametr: stan
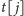 będzie reprezentować najlżejszą parę ścieżek rosnących, z których
jedna kończy się w wierzchołku
będzie reprezentować najlżejszą parę ścieżek rosnących, z których
jedna kończy się w wierzchołku
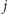 i wchodzi tam długą krawędzią,
natomiast druga kończy się w wierzchołku
i wchodzi tam długą krawędzią,
natomiast druga kończy się w wierzchołku
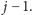 Oczywiście, ścieżki
muszą być rozłączne, pomijając wierzchołek 1, oraz muszą razem zawierać
wszystkie wierzchołki z zakresu
Oczywiście, ścieżki
muszą być rozłączne, pomijając wierzchołek 1, oraz muszą razem zawierać
wszystkie wierzchołki z zakresu
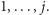 Przejścia pomiędzy stanami są
wyznaczone przez długie krawędzie. Dokładniej, długa krawędź z wierzchołka
Przejścia pomiędzy stanami są
wyznaczone przez długie krawędzie. Dokładniej, długa krawędź z wierzchołka
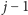 do wierzchołka
do wierzchołka
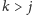 generuje przejście ze stanu
generuje przejście ze stanu
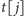 do stanu
do stanu
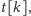 jeśli tylko istnieje sekwencja krawędzi
jednostkowych prowadzących z wierzchołka
jeśli tylko istnieje sekwencja krawędzi
jednostkowych prowadzących z wierzchołka
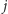 do wierzchołka
do wierzchołka

W tym algorytmie będziemy mieli co najwyżej tyle przejść między stanami,
ile jest długich krawędzi w grafie, a jedyne wyzwanie polega na tym, żeby
efektywnie symulować te przejścia. To już nie będzie trudne, będziemy to
wykonywać w czasie stałym. Musimy jedynie umieć sprawdzać, czy dwa
zadane wierzchołki są połączone sekwencją krawędzi jednostkowych, a jeśli tak,
to jaka jest suma wag tych krawędzi. Do tego celu wystarczą nam ciągi sum
częściowych dwóch ciągów: ciągu
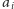 oznaczającego istnienie
krawędzi
oznaczającego istnienie
krawędzi
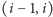 (jedynka, jeśli krawędź istnieje, zero, jeśli nie
istnieje) oraz ciągu
(jedynka, jeśli krawędź istnieje, zero, jeśli nie
istnieje) oraz ciągu
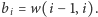 Oznaczmy przez
Oznaczmy przez
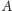 i
i
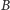 tablice reprezentujące odpowiednie ciągi sum częściowych (czyli
tablice reprezentujące odpowiednie ciągi sum częściowych (czyli
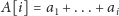 i analogicznie dla
i analogicznie dla
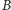 ). Tablice te łatwo
obliczamy w czasie
). Tablice te łatwo
obliczamy w czasie
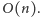 Wówczas przejście między stanami
Wówczas przejście między stanami
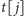 i
i
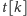 za pomocą długiej krawędzi
za pomocą długiej krawędzi
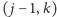 jest
możliwe, gdy
jest
możliwe, gdy
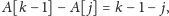 a waga tego przejścia to
a waga tego przejścia to
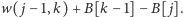
Ustalenie stanów początkowych i końcowych w usprawnionym programowaniu
dynamicznym pozostawiamy Czytelnikowi. Całe rozwiązanie działa w czasie
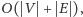 a zatem liniowo od rozmiaru wejścia.
a zatem liniowo od rozmiaru wejścia.