Informatyczny kącik olimpijski
Drogi
W tej edycji kącika znowu cofniemy się w czasie do 2005 roku, do pierwszej edycji konkursu Potyczki Algorytmiczne, i omówimy zadanie z finału próbnego tego konkursu pt. Drogi (bardzo podobne zadanie pojawiło się zresztą w jeszcze bardziej zamierzchłej przeszłości, na Międzynarodowej Olimpiadzie Informatycznej w 1996 roku).
Treść zadania jest bardzo prosta:
Zadanie. Do danego grafu skierowanego chcielibyśmy dołożyć możliwie najmniej krawędzi (skierowanych, rzecz jasna), tak by po tej operacji z każdego wierzchołka grafu dało się dojść do każdego innego wierzchołka. Innymi słowy, chcemy spowodować, żeby dany graf stał się silnie spójny.
Przy tak sformułowanym problemie naturalny wydaje się pomysł, aby dany
graf (oznaczmy go przez
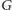 ) podzielić na silnie spójne składowe, tym
bardziej że tę operację możemy wykonać w czasie liniowym względem
rozmiaru grafu. Warto od razu pójść o krok dalej i przyjrzeć się grafowi
silnie spójnych składowych
) podzielić na silnie spójne składowe, tym
bardziej że tę operację możemy wykonać w czasie liniowym względem
rozmiaru grafu. Warto od razu pójść o krok dalej i przyjrzeć się grafowi
silnie spójnych składowych
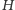 grafu
grafu
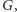 w którym każdej
silnie spójnej składowej grafu
w którym każdej
silnie spójnej składowej grafu
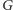 odpowiada jeden wierzchołek,
a krawędź między danymi dwoma wierzchołkami w
odpowiada jeden wierzchołek,
a krawędź między danymi dwoma wierzchołkami w
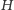 istnieje, gdy
odpowiadające im składowe w
istnieje, gdy
odpowiadające im składowe w
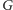 były połączone co najmniej jedną
krawędzią. Graf
były połączone co najmniej jedną
krawędzią. Graf
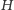 jest, oczywiście, acykliczny. Ponieważ w grafie
jest, oczywiście, acykliczny. Ponieważ w grafie
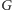 nie opłaca się nigdy dodawać krawędzi w ramach tej samej
silnie spójnej składowej, więc wynik dla grafu
nie opłaca się nigdy dodawać krawędzi w ramach tej samej
silnie spójnej składowej, więc wynik dla grafu
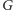 jest taki sam jak
dla grafu
jest taki sam jak
dla grafu
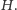 Odtąd będziemy zajmować się już tylko grafem
Odtąd będziemy zajmować się już tylko grafem
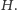
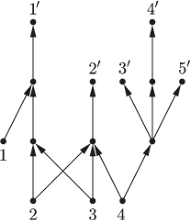
Rys. 1 Przykład grafu
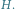 Mamy
Mamy
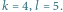
Po krótkim przyjrzeniu się grafowi
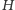 łatwo dostrzec pewne dolne
ograniczenie na liczbę krawędzi, które trzeba dodać. Oznaczmy przez
łatwo dostrzec pewne dolne
ograniczenie na liczbę krawędzi, które trzeba dodać. Oznaczmy przez
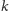 liczbę wierzchołków grafu
liczbę wierzchołków grafu
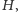 do których nie wchodzi żadna
krawędź, podobnie przez
do których nie wchodzi żadna
krawędź, podobnie przez
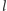 oznaczmy liczbę tych wierzchołków,
z których nie wychodzi żadna krawędź (patrz Rys. 1). Wspomnianym
ograniczeniem dolnym jest liczba
oznaczmy liczbę tych wierzchołków,
z których nie wychodzi żadna krawędź (patrz Rys. 1). Wspomnianym
ograniczeniem dolnym jest liczba
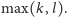 Faktycznie, aby z każdego
wierzchołka grafu
Faktycznie, aby z każdego
wierzchołka grafu
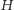 mogło się dać na końcu odwiedzić wszystkie
pozostałe wierzchołki grafu, z każdego wierzchołka musi wychodzić jakaś
krawędź; podobnie, do każdego wierzchołka musi wchodzić jakaś krawędź.
Jest tylko jeden wyjątek: jeśli graf
mogło się dać na końcu odwiedzić wszystkie
pozostałe wierzchołki grafu, z każdego wierzchołka musi wychodzić jakaś
krawędź; podobnie, do każdego wierzchołka musi wchodzić jakaś krawędź.
Jest tylko jeden wyjątek: jeśli graf
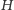 ma dokładnie jeden wierzchołek, to
ma dokładnie jeden wierzchołek, to
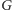 od początku był silnie spójny, więc nie musimy dodawać do niego
żadnych krawędzi.
od początku był silnie spójny, więc nie musimy dodawać do niego
żadnych krawędzi.
Przeanalizowanie kilku prostych przykładów pozwala dojść do
przeświadczenia, że aby graf acykliczny uczynić silnie spójnym, zawsze
wystarczy dodać
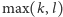 krawędzi. To pozwala zgadnąć, że nasze
dolne ograniczenie jest zarazem ograniczeniem górnym, co wystarcza do
wyznaczenia liczby potrzebnych krawędzi. My postawimy sobie ambitniejszy cel
i spróbujemy udowodnić nasze spostrzeżenie.
krawędzi. To pozwala zgadnąć, że nasze
dolne ograniczenie jest zarazem ograniczeniem górnym, co wystarcza do
wyznaczenia liczby potrzebnych krawędzi. My postawimy sobie ambitniejszy cel
i spróbujemy udowodnić nasze spostrzeżenie.

Rys. 2 Graf
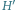 odpowiadający grafowi
odpowiadający grafowi
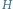 z rysunku 1.
z rysunku 1.
Skoro interesuje nas jedynie
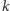 „dolnych” i
„dolnych” i
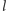 „górnych”
wierzchołków grafu
„górnych”
wierzchołków grafu
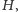 to stworzymy graf dwudzielny
to stworzymy graf dwudzielny
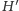 zawierający
tylko te wierzchołki. Wierzchołki
zawierający
tylko te wierzchołki. Wierzchołki
 i
i
 będą w grafie
będą w grafie
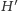 połączone krawędzią, jeśli w
połączone krawędzią, jeśli w
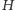 istniała między nimi
jakaś ścieżka (Rys. 2). Wynik, jaki otrzymamy dla
istniała między nimi
jakaś ścieżka (Rys. 2). Wynik, jaki otrzymamy dla
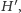 będzie
oczywiście taki sam jak wynik dla
będzie
oczywiście taki sam jak wynik dla
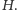 Załóżmy na razie, że
graf
Załóżmy na razie, że
graf
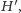 a więc też graf
a więc też graf
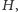 nie zawiera wierzchołków
izolowanych.
nie zawiera wierzchołków
izolowanych.
Pojawienie się grafu dwudzielnego naturalnie podsuwa pomysł, żeby w tym grafie znaleźć maksymalne skojarzenie (jak się dalej okaże, nie potrzebujemy wcale najliczniejszego skojarzenia, wystarczy nam dowolne maksymalne).

Rys. 3 Konstrukcja rozwiązania dla grafu
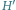 z rysunku 2. Pogrubione krawędzie biegnące
w górę to maksymalne skojarzenie w grafie
z rysunku 2. Pogrubione krawędzie biegnące
w górę to maksymalne skojarzenie w grafie
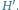
Jeśli graf
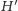 zawiera skojarzenie rozmiaru
zawiera skojarzenie rozmiaru
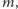 to wszystkie
wierzchołki skojarzone –
to wszystkie
wierzchołki skojarzone –
 dolnych i
dolnych i
 górnych – możemy
połączyć w cykl za pomocą
górnych – możemy
połączyć w cykl za pomocą
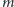 krawędzi poprowadzonych „na zakładkę”.
To stanowi dobrą bazę do konstrukcji całego rozwiązania. Musimy jeszcze tylko
w jakiś sposób dołączyć do tego cyklu nieskojarzone wierzchołki.
Możemy to zrobić następująco:
krawędzi poprowadzonych „na zakładkę”.
To stanowi dobrą bazę do konstrukcji całego rozwiązania. Musimy jeszcze tylko
w jakiś sposób dołączyć do tego cyklu nieskojarzone wierzchołki.
Możemy to zrobić następująco:
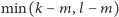 wierzchołków
nieskojarzonych łączymy w pary krawędziami biegnącymi w dół, a pozostałe
wierzchołki nieskojarzone (znajdujące się już tylko z jednej strony grafu)
dołączamy krawędziami bezpośrednio do cyklu – w przypadku wierzchołków
górnych używamy krawędzi skierowanych ku cyklowi, a w przeciwnym razie
używamy krawędzi skierowanych od cyklu (Rys. 3).
wierzchołków
nieskojarzonych łączymy w pary krawędziami biegnącymi w dół, a pozostałe
wierzchołki nieskojarzone (znajdujące się już tylko z jednej strony grafu)
dołączamy krawędziami bezpośrednio do cyklu – w przypadku wierzchołków
górnych używamy krawędzi skierowanych ku cyklowi, a w przeciwnym razie
używamy krawędzi skierowanych od cyklu (Rys. 3).
Spróbujmy uzasadnić poprawność tej konstrukcji. Przyjęliśmy, że
w grafie nie ma wierzchołków izolowanych, więc każdy górny nieskojarzony
wierzchołek jest połączony w
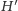 z jakimś dolnym wierzchołkiem
skojarzonym (nie mógłby to być dolny wierzchołek nieskojarzony, gdyż wtedy
moglibyśmy powiększyć skojarzenie). Symetryczne stwierdzenie zachodzi też
dla dolnych wierzchołków nieskojarzonych. To oznacza, że z cyklu da się
dojść do każdego z górnych wierzchołków nieskojarzonych, podobnie
z każdego z dolnych wierzchołków nieskojarzonych da się dojść do cyklu.
Teraz już łatwo sprawdzamy, że po dodaniu krawędzi biegnących w dół (oraz
tych łączących wierzchołki nieskojarzone bezpośrednio z cyklem) graf
z jakimś dolnym wierzchołkiem
skojarzonym (nie mógłby to być dolny wierzchołek nieskojarzony, gdyż wtedy
moglibyśmy powiększyć skojarzenie). Symetryczne stwierdzenie zachodzi też
dla dolnych wierzchołków nieskojarzonych. To oznacza, że z cyklu da się
dojść do każdego z górnych wierzchołków nieskojarzonych, podobnie
z każdego z dolnych wierzchołków nieskojarzonych da się dojść do cyklu.
Teraz już łatwo sprawdzamy, że po dodaniu krawędzi biegnących w dół (oraz
tych łączących wierzchołki nieskojarzone bezpośrednio z cyklem) graf
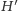 jest silnie spójny.
jest silnie spójny.
Na koniec warto przypomnieć sobie o wierzchołkach izolowanych w
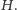 Ponieważ wliczają się one tak do dolnej, jak i do górnej grupy
w grafie
Ponieważ wliczają się one tak do dolnej, jak i do górnej grupy
w grafie
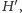 więc możemy je rozpatrzyć zupełnie osobno: najpierw
znaleźć rozwiązanie dla grafu bez tych wierzchołków, a następnie
umieścić je kolejno wewnątrz dowolnej z dodanych przez nas krawędzi.
Trzeba też dodatkowo rozpatrzyć przypadek szczególny, gdy w grafie
więc możemy je rozpatrzyć zupełnie osobno: najpierw
znaleźć rozwiązanie dla grafu bez tych wierzchołków, a następnie
umieścić je kolejno wewnątrz dowolnej z dodanych przez nas krawędzi.
Trzeba też dodatkowo rozpatrzyć przypadek szczególny, gdy w grafie
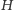 były same wierzchołki izolowane – wtedy po prostu łączymy je
wszystkie w cykl.
były same wierzchołki izolowane – wtedy po prostu łączymy je
wszystkie w cykl.
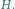 Mamy
Mamy
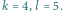
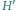 odpowiadający grafowi
odpowiadający grafowi
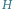 z rysunku 1.
z rysunku 1.
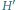 z rysunku 2. Pogrubione krawędzie biegnące
w górę to maksymalne skojarzenie w grafie
z rysunku 2. Pogrubione krawędzie biegnące
w górę to maksymalne skojarzenie w grafie