Informatyczny kącik olimpijski
Dziurawa szachownica
W tym miesiącu omówimy zadanie, które pojawiło się w pierwszej edycji konkursu Potyczki Algorytmiczne, w roku 2005.

Zadanie. Dana jest
szachownica o
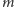 wierszach i
wierszach i
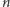 kolumnach
kolumnach
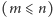 ,
mająca taki feler, że na niektórych jej polach znajdują się dziury. Obliczono,
na ile sposobów można na tej szachownicy rozstawić
,
mająca taki feler, że na niektórych jej polach znajdują się dziury. Obliczono,
na ile sposobów można na tej szachownicy rozstawić
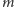 wież
tak, by żadna z wież nie stała na dziurawym polu i nie groziła zbiciem
innej (tzn. w każdej kolumnie może stać co najwyżej jedna wieża,
a w każdym wierszu stoi dokładnie jedna wieża). Należy wskazać te
pola szachownicy, w których można wywiercić dodatkowe dziury tak,
aby powyższa liczba ustawień nie zmieniła się. Przykładowa szachownica
została przedstawiona na poniższym rysunku. Krzyżykami oznaczono
dziurawe pola, zaś kolorem wyróżniono jedno z dwóch prawidłowych
rozmieszczeń wież. Dodatkowe dziury można zrobić na polach b1 oraz
a2.
wież
tak, by żadna z wież nie stała na dziurawym polu i nie groziła zbiciem
innej (tzn. w każdej kolumnie może stać co najwyżej jedna wieża,
a w każdym wierszu stoi dokładnie jedna wieża). Należy wskazać te
pola szachownicy, w których można wywiercić dodatkowe dziury tak,
aby powyższa liczba ustawień nie zmieniła się. Przykładowa szachownica
została przedstawiona na poniższym rysunku. Krzyżykami oznaczono
dziurawe pola, zaś kolorem wyróżniono jedno z dwóch prawidłowych
rozmieszczeń wież. Dodatkowe dziury można zrobić na polach b1 oraz
a2.
Zapewne niektórzy Czytelnicy od razu zorientują się, że pod płaszczykiem
terminologii szachowej kryje się problem, który możemy sprowadzić
do znajdowania skojarzeń w grafach dwudzielnych. Tak jest istotnie.
Rozważmy bowiem graf dwudzielny
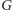 o
o
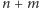 wierzchołkach:
wierzchołki ze zbioru
wierzchołkach:
wierzchołki ze zbioru
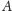 będą odpowiadać wierszom szachownicy,
natomiast wierzchołki ze zbioru
będą odpowiadać wierszom szachownicy,
natomiast wierzchołki ze zbioru
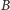 – kolumnom. Dwa wierzchołki
– kolumnom. Dwa wierzchołki
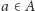 i
i
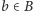 łączymy krawędzią wtedy, gdy na przecięciu wiersza
łączymy krawędzią wtedy, gdy na przecięciu wiersza
 i kolumny
i kolumny
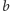 nie ma dziury. W takiej sytuacji poprawne
rozstawienie wież na szachownicy odpowiada skojarzeniu rozmiaru
nie ma dziury. W takiej sytuacji poprawne
rozstawienie wież na szachownicy odpowiada skojarzeniu rozmiaru
 w grafie
w grafie
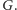 Treść zadania możemy więc przeformułować
następująco: należy znaleźć te krawędzie w grafie
Treść zadania możemy więc przeformułować
następująco: należy znaleźć te krawędzie w grafie
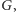 które nie
należą do żadnego skojarzenia rozmiaru
które nie
należą do żadnego skojarzenia rozmiaru
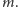
To prowadzi nas do pierwszego rozwiązania. Dla każdego niedziurawego pola
szachownicy
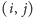 wykonujemy następujące sprawdzenie: stawiamy na
nim wieżę i próbujemy rozstawić
wykonujemy następujące sprawdzenie: stawiamy na
nim wieżę i próbujemy rozstawić
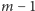 wież na pozostałej
części szachownicy, uruchamiając algorytm wyznaczania najliczniejszego
skojarzenia w grafie dwudzielnym. Rozwiązanie to można przyspieszyć:
zamiast za każdym razem od nowa znajdować najliczniejsze skojarzenie,
możemy zacząć od poprzednio znalezionego. W tym celu usuwamy wieże
z wiersza
wież na pozostałej
części szachownicy, uruchamiając algorytm wyznaczania najliczniejszego
skojarzenia w grafie dwudzielnym. Rozwiązanie to można przyspieszyć:
zamiast za każdym razem od nowa znajdować najliczniejsze skojarzenie,
możemy zacząć od poprzednio znalezionego. W tym celu usuwamy wieże
z wiersza
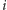 i kolumny
i kolumny
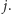 Za każdym razem wystarczy
zatem ustawić co najwyżej dwie brakujące wieże, czyli znaleźć co
najwyżej dwie ścieżki powiększające skojarzenie. Złożoność czasowa to
Za każdym razem wystarczy
zatem ustawić co najwyżej dwie brakujące wieże, czyli znaleźć co
najwyżej dwie ścieżki powiększające skojarzenie. Złożoność czasowa to
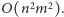
Podamy teraz lepsze rozwiązanie. Na początek znajdujemy w grafie
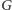 dowolne skojarzenie rozmiaru
dowolne skojarzenie rozmiaru
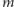 (jeśli takie skojarzenie nie
istnieje, to można wywiercić dziury we wszystkich polach). Tworzymy teraz
graf skierowany
(jeśli takie skojarzenie nie
istnieje, to można wywiercić dziury we wszystkich polach). Tworzymy teraz
graf skierowany
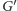 o takim samym zbiorze wierzchołków co
o takim samym zbiorze wierzchołków co
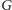 i następujących krawędziach:
i następujących krawędziach:
- (1)
- krawędzie, które
w grafie
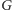 należały do znalezionego skojarzenia, kierujemy od
należały do znalezionego skojarzenia, kierujemy od
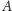 do
do
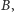
- (2)
- pozostałe krawędzie z
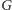 kierujemy od
kierujemy od
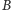 do
do
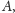
- (3)
- dodajemy krawędzie z wszystkich skojarzonych wierzchołków w
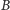 do wszystkich nieskojarzonych wierzchołków w
do wszystkich nieskojarzonych wierzchołków w
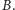
Następnie znajdujemy silnie spójne składowe w grafie
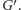 Okazuje się,
że krawędzie, które nie należą do żadnego skojarzenia rozmiaru
Okazuje się,
że krawędzie, które nie należą do żadnego skojarzenia rozmiaru
 w grafie
w grafie
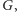 to te krawędzie typu (2) w grafie
to te krawędzie typu (2) w grafie
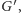 które
łączą dwie różne silnie spójne składowe. Spróbujmy to uzasadnić.
które
łączą dwie różne silnie spójne składowe. Spróbujmy to uzasadnić.
Stosunkowo łatwo wykazać, że pozostałe krawędzie typu (2) należą do
pewnego skojarzenia. Rozważmy taką krawędź
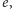 która leży
wewnątrz pewnej silnie spójnej składowej, zatem leży ona na pewnym cyklu.
Cykl ten może składać się z naprzemiennych krawędzi typu (1) i (2) lub
może zawierać krawędzie typu (3). W pierwszym przypadku do skojarzenia
zamiast krawędzi typu (1) z cyklu bierzemy krawędzie typu (2) i uzyskujemy
nowe skojarzenie zawierające krawędź
która leży
wewnątrz pewnej silnie spójnej składowej, zatem leży ona na pewnym cyklu.
Cykl ten może składać się z naprzemiennych krawędzi typu (1) i (2) lub
może zawierać krawędzie typu (3). W pierwszym przypadku do skojarzenia
zamiast krawędzi typu (1) z cyklu bierzemy krawędzie typu (2) i uzyskujemy
nowe skojarzenie zawierające krawędź
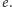 W drugim przypadku
rozważamy najdłuższą ścieżkę cyklu zawierającą
W drugim przypadku
rozważamy najdłuższą ścieżkę cyklu zawierającą
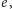 a niezawierającą
krawędzi typu (3). Ścieżka ta składa się na zmianę z krawędzi typu
(1) i (2) oraz zaczyna się w wierzchołku nieskojarzonym, a kończy
w skojarzonym. Znowu więc odwrócenie rolami krawędzi typu (1) i (2) załatwia
sprawę.
a niezawierającą
krawędzi typu (3). Ścieżka ta składa się na zmianę z krawędzi typu
(1) i (2) oraz zaczyna się w wierzchołku nieskojarzonym, a kończy
w skojarzonym. Znowu więc odwrócenie rolami krawędzi typu (1) i (2) załatwia
sprawę.
Rozważmy teraz krawędź
 (z
(z
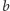 do
do
 ) typu (2), która
łączy w
) typu (2), która
łączy w
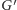 dwie różne silnie spójne składowe. Wszystkie wierzchołki
w
dwie różne silnie spójne składowe. Wszystkie wierzchołki
w
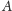 są skojarzone, niech więc
są skojarzone, niech więc
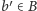 będzie wierzchołkiem
skojarzonym z
będzie wierzchołkiem
skojarzonym z
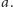 Oznaczmy przez
Oznaczmy przez
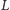 zbiór tych wierzchołków,
z których można dojść do wierzchołka
zbiór tych wierzchołków,
z których można dojść do wierzchołka
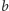 (w szczególności
(w szczególności
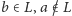 ). Wszystkie wierzchołki w
). Wszystkie wierzchołki w
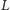 są skojarzone,
w przeciwnym przypadku taki nieskojarzony wierzchołek musiałby być w
są skojarzone,
w przeciwnym przypadku taki nieskojarzony wierzchołek musiałby być w
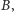 zatem prowadziłaby do niego krawędź typu (3) z
zatem prowadziłaby do niego krawędź typu (3) z
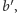 czyli
krawędź
czyli
krawędź
 leżałaby wewnątrz silnie spójnej składowej. Ponadto zbiory
leżałaby wewnątrz silnie spójnej składowej. Ponadto zbiory
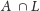 i
i
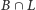 są równoliczne i skojarzone między sobą oraz
żaden z wierzchołków
są równoliczne i skojarzone między sobą oraz
żaden z wierzchołków
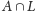 nie jest połączony z wierzchołkami spoza
nie jest połączony z wierzchołkami spoza
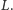 Innymi słowy, wszystkie wierzchołki z
Innymi słowy, wszystkie wierzchołki z
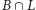 są potrzebne do
skojarzenia wierzchołków z
są potrzebne do
skojarzenia wierzchołków z
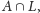 zatem w najliczniejszym skojarzeniu
żaden nie może być skojarzony przez krawędź
zatem w najliczniejszym skojarzeniu
żaden nie może być skojarzony przez krawędź
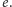 To kończy
dowód.
To kończy
dowód.
Na złożoność czasową rozwiązania składa się znalezienie najliczniejszego
skojarzenia w
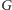 i wyznaczenie silnie spójnych składowych w
i wyznaczenie silnie spójnych składowych w
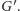 Pierwszy krok można wykonać w czasie
Pierwszy krok można wykonać w czasie
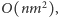 korzystając
z metody ścieżek naprzemiennych, lub w czasie
korzystając
z metody ścieżek naprzemiennych, lub w czasie
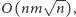 korzystając
z algorytmu Hopcrofta–Karpa.
korzystając
z algorytmu Hopcrofta–Karpa.
Drugi krok można wykonać za pomocą dwóch przeszukań grafu w głąb.
Jako ćwiczenie dla Czytelnika pozostawiamy pokazanie, że można to zrobić
w czasie
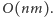 Kłopot stanowią krawędzie typu (3), których
może być rzędu
Kłopot stanowią krawędzie typu (3), których
może być rzędu
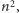 należy zatem wykorzystać ich regularną
strukturę.
należy zatem wykorzystać ich regularną
strukturę.