Ucieczka
Wyobraź sobie, Drogi Czytelniku, że jesteś kapitanem okrętu wojennego i w trakcie jednej z misji znalazłeś się na środku morza leżącego na terytorium wroga. Wiesz, że wróg rozmieścił w tej strefie pewną (skończoną) liczbę radarów. Każdy radar ma określony zasięg, być może różny w przypadku różnych radarów, i jest w stanie wykryć każdy podejrzany obiekt, który znajdzie się w jego zasięgu. Naszym siłom wywiadowczym udało się wykraść plan rozmieszczenia radarów. Na jego podstawie chcesz stwierdzić, czy możesz wydostać się z wrogich wód niezauważony przez radary.
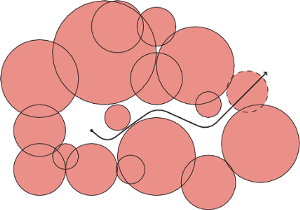
Powyższa historia wojenna z lotu ptaka wygląda następująco: na płaszczyźnie zadana jest pewna liczba kół stanowiących obszary zabronione. Dla uproszczenia nasz statek również przedstawimy jako koło. Naszym zadaniem jest sprawdzić, czy możemy przemieścić się statkiem nieskończenie daleko od początkowej pozycji, nie dotykając przy tym żadnego z pozostałych kół (Rys. 1).
Takie sformułowanie problemu nie jest jednak zbyt wygodne. Możemy je uprościć przez „odpompowanie” koła reprezentującego statek i „napompowanie” kół przedstawiających zasięgi radarów. Dokładniej, promienie wszystkich kół-radarów zwiększamy o promień statku, a sam statek zmniejszamy do jednego punktu – środka koła (Rys. 2). Aby uzasadnić poprawność tego przekształcenia, wystarczy zauważyć, że bezpieczna trasa statku charakteryzuje się tym, iż jego środek nie zbliża się do żadnego radaru na odległość mniejszą niż suma promienia statku i zasięgu radaru. Po tej transformacji dużo łatwiej udzielić odpowiedzi na pytanie postawione w zadaniu; w sytuacji z rysunku 2 ucieczka statku ewidentnie nie jest możliwa, ale gdyby np. nie było prawego górnego radaru, to można byłoby wskazać bezpieczną trasę ucieczki.
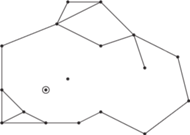
Rys. 3
A może dałoby się w ogóle pozbyć z problemu wszystkich kółek? Okazuje
się, że jest to możliwe. Intuicja jest taka, że pojedynczy radar bardzo łatwo
ominąć, ale za pomocą radarów, których zasięgi nachodzą na siebie, można
zbudować już bardzo skuteczną pułapkę. Przedstawmy więc całą sytuację jako
graf
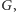 którego wierzchołki reprezentują lokalizacje radarów, a dwa
wierzchołki są połączone krawędzią, gdy zasięgi odpowiadających im
radarów przecinają się (Rys. 3). Nasz statek może opuścić terytorium
wroga wtedy i tylko wtedy, gdy nie jest otoczony żadnym cyklem grafu
którego wierzchołki reprezentują lokalizacje radarów, a dwa
wierzchołki są połączone krawędzią, gdy zasięgi odpowiadających im
radarów przecinają się (Rys. 3). Nasz statek może opuścić terytorium
wroga wtedy i tylko wtedy, gdy nie jest otoczony żadnym cyklem grafu
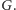
Rys. 4
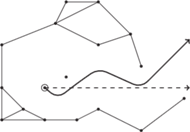
Uzasadnienie tego faktu w jedną stronę jest oczywiste: jeśli statek jest otoczony cyklem, to na pewno nigdy się z niego nie wydostanie. W drugą stronę trzeba się trochę bardziej nagimnastykować, bo nie każda trasa ucieczki „z grafu” faktycznie unika wszystkich radarów. Przykładowo, na rysunku 4 (przedstawiającym graf odpowiadający sytuacji bez prawego górnego radaru) trasa narysowana linią przerywaną nie przecina krawędzi grafu, ale nie jest bezpieczną trasą ucieczki. Poprawne uzasadnienie może wyglądać, na przykład, tak: dzielimy graf na spójne składowe i dla zbioru okręgów z każdej składowej wyznaczamy ich zewnętrzny obrys. Skoro statek nie jest otoczony żadnym cyklem grafu, to możemy nim dopłynąć do obrysu najbliższej składowej, a następnie przepłynąć do jakiegokolwiek punktu wzdłuż obrysu. Z któregoś takiego punktu będziemy mogli albo już bezpośrednio uciec w siną dal, albo przedostać się do obrysu innej składowej itd.
Rys. 5
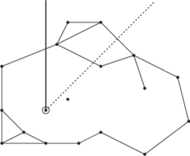
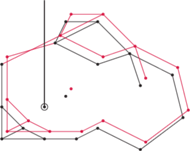
Pozostał nam już tylko problem stwierdzenia, czy statek znajduje się wewnątrz jakiegoś cyklu, czy też nie. W tym momencie ktoś mógłby przypomnieć sobie klasyczny algorytm sprawdzania, czy zadany punkt leży we wnętrzu danego wielokąta (niekoniecznie wypukłego). Aby to sprawdzić, wypuszczamy z tego punktu półprostą w losowym kierunku i zliczamy jej przecięcia z brzegiem wielokąta; jeśli jest ich nieparzyście wiele, to punkt leży wewnątrz wielokąta, a jeśli parzyście wiele, to na zewnątrz. Losowość kierunku gwarantuje, że półprosta nie przejdzie przez żaden wierzchołek wielokąta, dzięki czemu unikamy rozważania przykrych przypadków szczególnych. Niestety, w naszym problemie możemy mieć w grafie coś więcej niż jeden wielokąt, co powoduje, że zależnie od kierunku półprostej liczba przecięć może być parzysta bądź nieparzysta (Rys. 5). Klasyczny algorytm tutaj nie zadziała.
Warto jednak pozostać przy pomyśle z półprostą, tylko sprytniej go
wykorzystać. Chcemy stwierdzić, czy w grafie
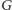 istnieje taki cykl, że
łączna liczba przecięć krawędzi tego cyklu z wybraną półprostą jest
nieparzysta. Krawędzie grafu przecinające półprostą zmieniają parzystość
licznika przecięć, oznaczymy je zatem jedynką, a pozostałe krawędzie
poetykietujemy zerami.
istnieje taki cykl, że
łączna liczba przecięć krawędzi tego cyklu z wybraną półprostą jest
nieparzysta. Krawędzie grafu przecinające półprostą zmieniają parzystość
licznika przecięć, oznaczymy je zatem jedynką, a pozostałe krawędzie
poetykietujemy zerami.
Rys. 6
Teraz przyszedł czas na kluczowy pomysł: stworzymy nowy graf
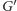 zawierający
dwie kopie oryginalnego grafu. Dokładniej, dla każdego wierzchołka
zawierający
dwie kopie oryginalnego grafu. Dokładniej, dla każdego wierzchołka
 grafu
grafu
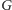 do grafu
do grafu
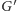 dodamy wierzchołki
dodamy wierzchołki
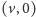 i
i
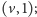 tutaj druga współrzędna oznacza parzystość liczby przecięć
z wybraną półprostą. Jeśli w grafie
tutaj druga współrzędna oznacza parzystość liczby przecięć
z wybraną półprostą. Jeśli w grafie
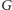 mamy krawędź łączącą
wierzchołki
mamy krawędź łączącą
wierzchołki
 i
i
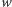 o etykiecie 0, to w grafie
o etykiecie 0, to w grafie
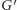 tworzymy
dwie krawędzie, łączące
tworzymy
dwie krawędzie, łączące
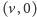 z
z
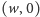 oraz
oraz
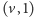 z
z
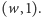 A jeśli rozważana krawędź grafu
A jeśli rozważana krawędź grafu
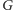 ma etykietę 1, to
w grafie
ma etykietę 1, to
w grafie
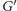 łączymy wierzchołki
łączymy wierzchołki
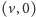 z
z
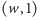 oraz
oraz
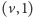 z
z
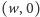 – patrz rysunek 6.
– patrz rysunek 6.
Był już kluczowy pomysł, teraz pora na kluczowe spostrzeżenie: cykl
złożony z krawędzi grafu
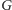 uniemożliwiający statkowi ucieczkę
w grafie
uniemożliwiający statkowi ucieczkę
w grafie
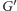 odpowiada po prostu ścieżce z jakiegoś wierzchołka
odpowiada po prostu ścieżce z jakiegoś wierzchołka
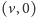 do
do
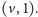 Wystarczy zatem stwierdzić, czy w grafie
Wystarczy zatem stwierdzić, czy w grafie
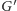 jakaś para wierzchołków postaci
jakaś para wierzchołków postaci
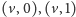 należy do tej
samej spójnej składowej. Nie trzeba wielkiego zacięcia algorytmicznego, by
uwierzyć, że sprawdzenie tak sformułowanego warunku nie może już być
trudne. Faktycznie, do podziału grafu na spójne składowe można zastosować
praktycznie dowolny algorytm przeszukiwania grafu, a najwygodniej –
przeszukiwanie w głąb. Ostateczne kryterium stwierdzające możliwość
ucieczki statku okazało się zatem niezbyt skomplikowane i, co ciekawe,
niespecjalnie związane z geometrią.
należy do tej
samej spójnej składowej. Nie trzeba wielkiego zacięcia algorytmicznego, by
uwierzyć, że sprawdzenie tak sformułowanego warunku nie może już być
trudne. Faktycznie, do podziału grafu na spójne składowe można zastosować
praktycznie dowolny algorytm przeszukiwania grafu, a najwygodniej –
przeszukiwanie w głąb. Ostateczne kryterium stwierdzające możliwość
ucieczki statku okazało się zatem niezbyt skomplikowane i, co ciekawe,
niespecjalnie związane z geometrią.