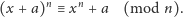Test na liczbę pierwszą
Chyba wszyscy lubimy liczby pierwsze. Szczególne wrażenie robią te naprawdę duże, wydają się skrywać w sobie jakąś nadzwyczajną tajemnicę: dlaczego akurat one stały się swego rodzaju wybrańcami spośród innych liczb i mają tak niezwykłe właściwości?
Matematycy od dawna zastanawiają się, jak sprawdzać, czy liczba jest pierwsza. Dawniej robili to tylko (a może aż) z ciekawości i poczucia doniosłości zadania. W dzisiejszych czasach mają także bardziej praktyczne motywacje. Przykładowo, na potrzeby algorytmu RSA chcielibyśmy umieć sprawdzać, czy liczba mająca około 500 cyfr jest pierwsza, czy też złożona.
Powszechnie stosowany i w praktyce najszybszy jest test pierwszości Millera–Rabina (w skrócie test MR), wymyślony w 1980 roku.
Wykorzystuje on losowość i opiera się na następującym pomyśle.
Powiedzmy, że chcemy sprawdzić, czy liczba
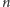 jest pierwsza. Okazuje
się, że jeżeli
jest pierwsza. Okazuje
się, że jeżeli
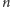 jest złożona, to co najmniej połowa liczb ze zbioru
jest złożona, to co najmniej połowa liczb ze zbioru
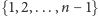 jest świadkami złożoności tej liczby (to zresztą bardzo
mało dokładne oszacowanie). Nazwa bierze się stąd, że jeżeli dla pewnej liczby
jest świadkami złożoności tej liczby (to zresztą bardzo
mało dokładne oszacowanie). Nazwa bierze się stąd, że jeżeli dla pewnej liczby
 istnieje liczba
istnieje liczba
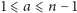 będąca jej świadkiem złożoności,
to wiadomo, że
będąca jej świadkiem złożoności,
to wiadomo, że
 jest liczbą złożoną.
jest liczbą złożoną.
Stosunkowo łatwo jest sprawdzić, czy dana liczba
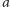 jest świadkiem
złożoności dla
jest świadkiem
złożoności dla
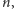 ale nie będziemy teraz wchodzić w szczegóły, co to
znaczy i jak się to robi. Co więcej, odpowiednie obliczenia można wykonać
szybko – jeżeli liczba
ale nie będziemy teraz wchodzić w szczegóły, co to
znaczy i jak się to robi. Co więcej, odpowiednie obliczenia można wykonać
szybko – jeżeli liczba
 ma
ma
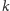 cyfr, to algorytm sprawdzający, czy
cyfr, to algorytm sprawdzający, czy
 jest świadkiem złożoności dla
jest świadkiem złożoności dla
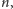 wykonuje mniej więcej
wykonuje mniej więcej
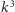 operacji. To znaczy, że dla
operacji. To znaczy, że dla
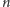 będącej liczbą pięćsetcyfrową
wykona on mniej więcej
będącej liczbą pięćsetcyfrową
wykona on mniej więcej
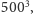 czyli 125 milionów operacji. Nasz
domowy komputer potrzebuje na to mniej więcej jednej setnej sekundy – czyli nie
jest źle.
czyli 125 milionów operacji. Nasz
domowy komputer potrzebuje na to mniej więcej jednej setnej sekundy – czyli nie
jest źle.
Zatem aby sprawdzić, czy liczba
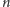 jest pierwsza, postępujemy tak: losujemy
jest pierwsza, postępujemy tak: losujemy
 z przedziału od 1 do
z przedziału od 1 do
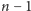 i sprawdzamy, czy
i sprawdzamy, czy
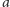 jest
świadkiem złożoności dla
jest
świadkiem złożoności dla
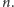 Jeżeli jest, to wiemy, że
Jeżeli jest, to wiemy, że
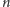 jest
złożona. Jeśli nie, to
jest
złożona. Jeśli nie, to
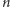 przeszła pierwszą próbę i sprawdzamy
dalej. Ponieważ dla dowolnego
przeszła pierwszą próbę i sprawdzamy
dalej. Ponieważ dla dowolnego
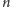 świadkowie złożoności
to przynajmniej połowa liczb z przedziału od 1 do
świadkowie złożoności
to przynajmniej połowa liczb z przedziału od 1 do
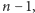 więc
prawdopodobieństwo, że liczba złożona
więc
prawdopodobieństwo, że liczba złożona
 przejdzie pojedynczą
próbę, jest nie większe niż
przejdzie pojedynczą
próbę, jest nie większe niż
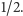 Losujemy więc kolejne
Losujemy więc kolejne
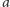 i znów
sprawdzamy, czy jest ono świadkiem złożoności dla
i znów
sprawdzamy, czy jest ono świadkiem złożoności dla
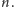 Jeżeli liczba
Jeżeli liczba
 jest złożona, to prawdopodobieństwo przejścia 30 testów bez
znalezienia świadka złożoności jest mniejsze niż
jest złożona, to prawdopodobieństwo przejścia 30 testów bez
znalezienia świadka złożoności jest mniejsze niż
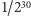 (czyli
również mniejsze niż
(czyli
również mniejsze niż
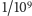 ). Po 100 testach prawdopodobieństwo
tego, że błędnie uznamy liczbę złożoną za pierwszą, jest już mniejsze
niż szansa na to, że w ciągu następnej minuty wielki meteoryt uderzy
w Ziemię i zakończy wszelkie nasze matematyczne dywagacje. Czyli
mamy pewność zupełnie wystarczającą. Przeprowadzenie 100 testów
zajmie na domowym komputerze nie więcej niż sekundę – to bardzo
niewiele.
). Po 100 testach prawdopodobieństwo
tego, że błędnie uznamy liczbę złożoną za pierwszą, jest już mniejsze
niż szansa na to, że w ciągu następnej minuty wielki meteoryt uderzy
w Ziemię i zakończy wszelkie nasze matematyczne dywagacje. Czyli
mamy pewność zupełnie wystarczającą. Przeprowadzenie 100 testów
zajmie na domowym komputerze nie więcej niż sekundę – to bardzo
niewiele.
Matematykom jednak problem testowania pierwszości nadal nie dawał spokoju. Chcieli mieć metodę dającą pewność absolutną, obliczającą wynik w sensownym czasie, a nie tylko wystarczającą do celów praktycznych.
Powiemy, że algorytm jest wielomianowy, jeżeli dla danych rozmiaru
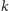 wykonuje co najwyżej
wykonuje co najwyżej
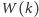 operacji, gdzie
operacji, gdzie
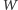 to pewien
wielomian. Czyli, na przykład, test MR jest algorytmem wielomianowym, gdyż
dla liczby o
to pewien
wielomian. Czyli, na przykład, test MR jest algorytmem wielomianowym, gdyż
dla liczby o
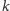 cyfrach wykonuje co najwyżej
cyfrach wykonuje co najwyżej
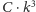 operacji dla
pewnej stałej
operacji dla
pewnej stałej
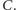
Algorytmy wielomianowe są umownie uważane za szybkie, a te o większej złożoności – za wolne. W informatyce teoretycznej dla danego problemu bardzo ważnym pytaniem jest, czy da się skonstruować algorytm wielomianowy rozwiązujący go, który podaje poprawną odpowiedź zawsze, a nie tylko z dużym prawdopodobieństwem. Dla problemu testowania pierwszości pytanie to do niedawna było problemem otwartym. Test MR nie jest rozwiązaniem, ponieważ zawiera element losowości.
Chociaż przez wiele lat nie udawało się znaleźć odpowiedzi, większość
matematyków wierzyła w istnienie wielomianowego testu pierwszości. Aż
wreszcie w roku 2002 trzech naukowców z Uniwersytetu w Kampurze ogłosiło
znalezienie pierwszego takiego algorytmu. Nazwano go algorytmem AKS, od
pierwszych liter nazwisk twórców: Agrawal, Kayal, Saxena. To był wielki sukces
– kwestia trudności testowania pierwszości została ostatecznie rozstrzygnięta.
Autorzy otrzymali za to osiągnięcie m.in. nagrodę Gödla – najbardziej
prestiżowe wyróżnienie w dziedzinie informatyki teoretycznej. Co ciekawe,
test AKS działa w praktyce wolniej niż test MR. Po pewnych poprawkach dla
liczby o
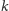 cyfrach wykonuje rzędu
cyfrach wykonuje rzędu
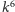 operacji, a oryginalny
algorytm jest nawet jeszcze nieco wolniejszy. To nie umniejsza jednak
doniosłości wyniku.
operacji, a oryginalny
algorytm jest nawet jeszcze nieco wolniejszy. To nie umniejsza jednak
doniosłości wyniku.
Opis algorytmu mieści się na zaledwie kilku stronach, co jest zupełnie niespotykane dla osiągnięć matematycznych tej trudności. Co więcej, używa (po paru poprawkach) jedynie elementarnej matematyki. Opiera się na kilku bardzo sprytnych spostrzeżeniach. Korzystając z okazji, przyjrzyjmy się temu algorytmowi z lotu ptaka. Głównym pomysłem jest następujące spostrzeżenie.
Dowód. Kongruencję z lematu rozumiemy jako równość modulo
 współczynników przy odpowiednich potęgach
współczynników przy odpowiednich potęgach
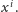 W wyrażeniu
W wyrażeniu
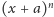 współczynnik przy
współczynnik przy
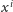 to
to
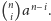 Wystarczy więc zastanowić się, kiedy
Wystarczy więc zastanowić się, kiedy
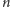 dzieli
dzieli
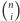 dla
dla
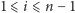 oraz czy
oraz czy
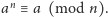 Gdy
Gdy
 jest pierwsza, to łatwo sprawdzić,
że liczby
jest pierwsza, to łatwo sprawdzić,
że liczby
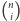 oraz
oraz
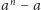 są podzielne przez
są podzielne przez
 (ten
ostatni fakt to małe twierdzenie Fermata), więc teza jest prawdziwa.
(ten
ostatni fakt to małe twierdzenie Fermata), więc teza jest prawdziwa.
Przypuśćmy teraz, że
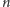 jest
złożona i liczba pierwsza
jest
złożona i liczba pierwsza
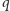 dzieli
dzieli
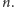 Niech
Niech
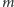 będzie
takim maksymalnym wykładnikiem, że
będzie
takim maksymalnym wykładnikiem, że
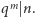 Wówczas jednak
mamy
Wówczas jednak
mamy

gdyż
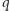 dzieli licznik w
dzieli licznik w
 -tej potędze, a mianownik
w pierwszej. Liczba
-tej potędze, a mianownik
w pierwszej. Liczba
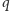 jest względnie pierwsza z
jest względnie pierwsza z
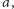 czyli
czyli
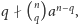 a zatem
a zatem
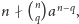 co dowodzi tezy
również dla liczb złożonych.
co dowodzi tezy
również dla liczb złożonych.
By rozstrzygnąć, czy
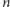 jest pierwsze, wystarczy więc sprawdzić, czy
wielomiany
jest pierwsze, wystarczy więc sprawdzić, czy
wielomiany
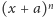 i
i
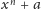 mają wszystkie współczynniki
przystające modulo
mają wszystkie współczynniki
przystające modulo
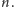 Gdybyśmy jednak sprawdzali je po kolei
przy każdej potędze
Gdybyśmy jednak sprawdzali je po kolei
przy każdej potędze
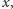 to wykonalibyśmy przynajmniej rzędu
to wykonalibyśmy przynajmniej rzędu
 operacji. To za dużo, więc trzeba obliczać współczynniki
sprytnie.
operacji. To za dużo, więc trzeba obliczać współczynniki
sprytnie.
Kolejny pomysł to sprawdzanie równości (1) modulo wielomian postaci
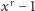 dla pewnego
dla pewnego
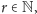 czyli
czyli
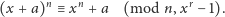 | (2) |
Może się jednak okazać, że niektóre liczby złożone spełniają równość
(2), mimo że nie spełniają równości (1). Rozwiązaniem tego problemu jest
sprawdzanie (2) dla odpowiednio dobranego
 i dla wszystkich
dodatnich wartości
i dla wszystkich
dodatnich wartości
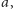 nie większych niż
nie większych niż
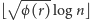 (gdzie
(gdzie
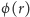 oznacza liczbę liczb mniejszych od
oznacza liczbę liczb mniejszych od
 i względnie pierwszych
z
i względnie pierwszych
z
 ). Okazuje się, że liczba
). Okazuje się, że liczba
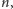 spełniająca wszystkie takie
równości, musi być pierwsza. Właśnie w wykazaniu prawdziwości tego
spostrzeżenia leży główna trudność techniczna dowodu.
spełniająca wszystkie takie
równości, musi być pierwsza. Właśnie w wykazaniu prawdziwości tego
spostrzeżenia leży główna trudność techniczna dowodu.
Niech
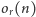 będzie taką najmniejszą liczbą
będzie taką najmniejszą liczbą
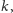 że
że
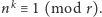 Algorytm AKS działa według następującego schematu:
Algorytm AKS działa według następującego schematu:
- 1.
- jeśli
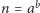 dla
dla
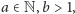 to zwróć ZŁOŻONA
to zwróć ZŁOŻONA
- 2.
- znajdź taką najmniejszą liczbę
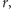 że
że
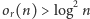
- 3.
- jeśli
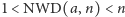 dla jakiegoś
dla jakiegoś
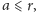 to zwróć
ZŁOŻONA
to zwróć
ZŁOŻONA
- 4.
- jeśli
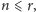 to zwróć PIERWSZA
to zwróć PIERWSZA
- 5.
- dla
 od
od
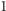 do
do
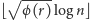 wykonuj: jeśli
wykonuj: jeśli
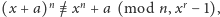 to zwróć ZŁOŻONA
to zwróć ZŁOŻONA
- 6.
- zwróć PIERWSZA
Bez wielkiej trudności można stwierdzić, że jeśli algorytm zakończy działanie
w jednym z pierwszych pięciu kroków, to odpowiedź jest poprawna. Jeżeli
zwróci wynik w punkcie 1, to zrobi, oczywiście, słusznie. Jeżeli znajdzie
w punkcie 3 taką liczbę
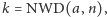 że
że
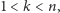 to
to
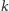 jest nietrywialnym dzielnikiem
jest nietrywialnym dzielnikiem
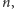 czyli istotnie
czyli istotnie
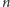 jest
złożona. Z kolei jeżeli w punkcie 4 okaże się, że
jest
złożona. Z kolei jeżeli w punkcie 4 okaże się, że
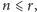 to znaczy,
że w punkcie 3 sprawdziliśmy wszystkie
to znaczy,
że w punkcie 3 sprawdziliśmy wszystkie
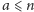 i każda była
względnie pierwsza z
i każda była
względnie pierwsza z
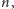 czyli faktycznie
czyli faktycznie
 jest pierwsza. Jeśli
w punkcie 5 równość modulo
jest pierwsza. Jeśli
w punkcie 5 równość modulo
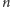 nie jest spełniona, to nie zachodzi
również zależność (1), czyli istotnie
nie jest spełniona, to nie zachodzi
również zależność (1), czyli istotnie
 jest złożona. Pozostaje jedna
wątpliwość co do poprawności algorytmu: czy wynik zwracany w punkcie
6 jest poprawny?
jest złożona. Pozostaje jedna
wątpliwość co do poprawności algorytmu: czy wynik zwracany w punkcie
6 jest poprawny?
Dowód opiera się na analizie funkcji
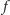 oraz liczb
oraz liczb
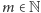 spełniających
równanie
spełniających
równanie

dla pewnego konkretnego czynnika pierwszego
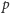 liczby
liczby
 Jeśli
liczba
Jeśli
liczba
 przeszła testy w punkcie 5, to dla każdej funkcji postaci
przeszła testy w punkcie 5, to dla każdej funkcji postaci
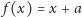 oraz
oraz
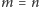 powyższa kongruencja jest prawdziwa.
Można wyprowadzić analogiczne zależności dla innych funkcji
powyższa kongruencja jest prawdziwa.
Można wyprowadzić analogiczne zależności dla innych funkcji
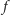 i liczb
i liczb
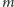 i, idąc tym tropem, udowodnić, że algorytm
słusznie zwraca wynik PIERWSZA w punkcie 6. To rozumowanie pozwala
zakończyć dowód poprawności algorytmu, ale wymaga trochę pracy nad
szczegółami.
i, idąc tym tropem, udowodnić, że algorytm
słusznie zwraca wynik PIERWSZA w punkcie 6. To rozumowanie pozwala
zakończyć dowód poprawności algorytmu, ale wymaga trochę pracy nad
szczegółami.
Czytelnik Uważny chciałby pewnie zapytać, czy istotnie algorytm AKS jest
wielomianowy. Tę sprawę rozwiązuje lemat, z którego wynika, że dla
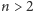 istnieje
istnieje
 nie większe niż
nie większe niż
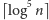 spełniające
własność z drugiego kroku algorytmu. Analizując dokładnie dalsze kroki (do
czego przydaje się pewne doświadczenie w szacowaniu złożoności),
zauważymy, że ten fakt rzeczywiście pozwala na oszacowanie czasu działania
algorytmu przez wielomian zależny od
spełniające
własność z drugiego kroku algorytmu. Analizując dokładnie dalsze kroki (do
czego przydaje się pewne doświadczenie w szacowaniu złożoności),
zauważymy, że ten fakt rzeczywiście pozwala na oszacowanie czasu działania
algorytmu przez wielomian zależny od
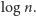 Dobrym zadaniem na
początek jest znalezienie sposobu wykonania pierwszego kroku w czasie
wielomianowym od
Dobrym zadaniem na
początek jest znalezienie sposobu wykonania pierwszego kroku w czasie
wielomianowym od
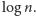
Te wyniki nie oznaczają bynajmniej, że cała sprawa liczb pierwszych doczekała się ostatecznego zamknięcia. Istnieje naprawdę ogromnie dużo nierozwiązanych problemów dotyczących liczb pierwszych. Wiele z nich ma także znaczenie praktyczne. Chyba najważniejszym takim problemem jest zagadnienie faktoryzacji liczb, czyli znajdowania ich rozkładu na czynniki pierwsze. Do dziś nie ma dla tego problemu żadnych algorytmów działających w zadowalającym czasie, choćby takich, które wykorzystują losowość, albo nawet takich, które wydają się poprawne, ale na razie nie umiemy tego udowodnić.