Informatyczny kącik olimpijski
Robot sortujący
Tym razem omówimy zadanie Robot sortujący (ang. Robotic Sort) z Mistrzostw Europy Środkowej w Programowaniu Zespołowym 2007 (CERC 2007).
W zadaniu występuje nietypowy algorytm sortowania
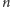 -elementowego
ciągu liczb całkowitych. W
-elementowego
ciągu liczb całkowitych. W
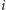 -tym kroku (dla
-tym kroku (dla
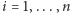 )
znajdujemy w ciągu
)
znajdujemy w ciągu
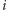 -ty najmniejszy element; załóżmy, że znajduje się
on na pozycji
-ty najmniejszy element; załóżmy, że znajduje się
on na pozycji
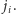 Następnie odwracamy fragment ciągu znajdujący się
między pozycjami
Następnie odwracamy fragment ciągu znajdujący się
między pozycjami
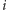 -tą a
-tą a
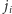 -tą i w ten sposób rozważany element
trafia na docelową pozycję w posortowanym ciągu. Naszym zadaniem jest
efektywnie zasymulować ten algorytm, a dokładniej, wyznaczyć ciąg pozycji
-tą i w ten sposób rozważany element
trafia na docelową pozycję w posortowanym ciągu. Naszym zadaniem jest
efektywnie zasymulować ten algorytm, a dokładniej, wyznaczyć ciąg pozycji
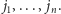 Przykładowo, jeśli ciągiem do posortowania jest 3, 4, 5, 1, 6, 2,
to wynikowy ciąg pozycji odpowiadających prawym końcom kolejnych
odwróceń to 4, 6, 4, 5, 6, 6. Dla uproszczenia założymy, że wyjściowy ciąg
jest permutacją liczb
Przykładowo, jeśli ciągiem do posortowania jest 3, 4, 5, 1, 6, 2,
to wynikowy ciąg pozycji odpowiadających prawym końcom kolejnych
odwróceń to 4, 6, 4, 5, 6, 6. Dla uproszczenia założymy, że wyjściowy ciąg
jest permutacją liczb
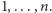 W oryginalnym zadaniu ciąg nie musiał
być różnowartościowy, ale sprowadzenie ogólnego przypadku do
przypadku permutacji jest całkiem proste.
W oryginalnym zadaniu ciąg nie musiał
być różnowartościowy, ale sprowadzenie ogólnego przypadku do
przypadku permutacji jest całkiem proste.
Bezpośrednia implementacja algorytmu sortowania przez odwracanie ma
złożoność czasową
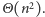 Można się o tym przekonać,
sprawdzając działanie algorytmu dla ciągu 2, 4, 6, 8,
Można się o tym przekonać,
sprawdzając działanie algorytmu dla ciągu 2, 4, 6, 8,
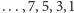 –
właśnie w tym przypadku wykonujemy największą liczbę operacji.
–
właśnie w tym przypadku wykonujemy największą liczbę operacji.
W takim razie spróbujemy zastosować jakieś inne podejście. Ponumerujmy
elementy ciągu po kolei, od lewej do prawej, od 1 do
 Załóżmy, że
najmniejszy element ciągu znajduje się na pozycji
Załóżmy, że
najmniejszy element ciągu znajduje się na pozycji
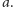 Wówczas po
pierwszym odwróceniu elementy ciągu będą ustawione w następującej
kolejności:
Wówczas po
pierwszym odwróceniu elementy ciągu będą ustawione w następującej
kolejności:

Widzimy, że tak naprawdę struktura ciągu zmieniła się dosyć nieznacznie.
Jeśli teraz drugi najmniejszy element znajdował się, przykładowo, na pozycji
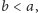 to po drugim odwróceniu ciąg będzie miał postać:
to po drugim odwróceniu ciąg będzie miał postać:

Domyślamy się już, co będzie dalej. Po
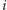 -tym odwróceniu ciąg będzie
miał postać
-tym odwróceniu ciąg będzie
miał postać

dla pewnego
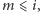 przy czym
przy czym
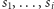 to numery
to numery
 najmniejszych elementów ciągu, zaś
najmniejszych elementów ciągu, zaś
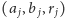 oznacza ciąg
liczb
oznacza ciąg
liczb
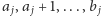 ustawionych w takim właśnie porządku (jeśli
ustawionych w takim właśnie porządku (jeśli
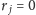 ) lub odwrotnie, malejąco (jeśli
) lub odwrotnie, malejąco (jeśli
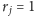 ).
).
Zauważmy, że używając takiej reprezentacji, kolejne odwrócenie
w ciągu możemy wykonać w czasie
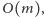 o ile tylko będziemy
dla każdego elementu
o ile tylko będziemy
dla każdego elementu
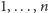 pamiętać, na której pozycji
wyjściowego ciągu się znajdował (oznaczenie:
pamiętać, na której pozycji
wyjściowego ciągu się znajdował (oznaczenie:
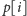 ). Załóżmy, że
). Załóżmy, że
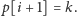 Znajdujemy teraz taką grupę
Znajdujemy teraz taką grupę
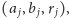 że
że
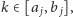 rozbijamy ją na dwie, a następnie między te dwie części
wstawiamy, odwrócone, wszystkie wcześniejsze grupy. Przykładowo, jeśli
rozbijamy ją na dwie, a następnie między te dwie części
wstawiamy, odwrócone, wszystkie wcześniejsze grupy. Przykładowo, jeśli
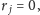 to wynikowy ciąg ma postać:
to wynikowy ciąg ma postać:

Przypadek
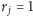 rozpatrujemy analogicznie. Po każdej
operacji przybywa co najwyżej jedna grupa – być może zero, jeśli
rozpatrujemy analogicznie. Po każdej
operacji przybywa co najwyżej jedna grupa – być może zero, jeśli
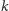 znajdowało się na skraju grupy
znajdowało się na skraju grupy
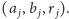 To jednak
oznacza, że liczba grup może rosnąć liniowo, więc koszt czasowy całego
algorytmu może być rzędu
To jednak
oznacza, że liczba grup może rosnąć liniowo, więc koszt czasowy całego
algorytmu może być rzędu
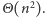 Pozostawiamy Czytelnikowi
znalezienie złośliwego przykładu, wymuszającego wykonanie takiej liczby
operacji – co ciekawe, poprzednio podany złośliwy przykład nie ma tej
własności.
Pozostawiamy Czytelnikowi
znalezienie złośliwego przykładu, wymuszającego wykonanie takiej liczby
operacji – co ciekawe, poprzednio podany złośliwy przykład nie ma tej
własności.
Mogłoby się wydawać, że ponieśliśmy porażkę – tyle wysiłku, a na
końcu i tak algorytm jest kwadratowy. Możemy jednak osiągnąć lepszą
złożoność czasową, jeśli tylko dostrzeżemy mocną stronę naszego
algorytmu: otóż na samym początku jest on bardzo szybki. Koszt pierwszych
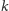 kroków algorytmu to
kroków algorytmu to
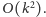 Przyjmijmy
Przyjmijmy
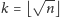 ;
wówczas podane kroki wykonujemy w czasie
;
wówczas podane kroki wykonujemy w czasie
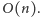 Kolejne kroki
byłyby bardziej kosztowne, dlatego zamiast nich zrobimy... porządek. Możemy
mianowicie wypisać explicite wszystkie wyrazy ciągu powstałego po
Kolejne kroki
byłyby bardziej kosztowne, dlatego zamiast nich zrobimy... porządek. Możemy
mianowicie wypisać explicite wszystkie wyrazy ciągu powstałego po
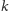 odwróceniach, ponumerować je kolejno, wyznaczyć od nowa tablicę
indeksów poszczególnych elementów w ciągu
odwróceniach, ponumerować je kolejno, wyznaczyć od nowa tablicę
indeksów poszczególnych elementów w ciągu
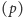 i kolejne
odwrócenia wykonywać już za pomocą nowego ciągu.
i kolejne
odwrócenia wykonywać już za pomocą nowego ciągu.
Uporządkowanie ciągu po
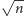 odwróceniach zajmuje czas
odwróceniach zajmuje czas
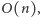 taki sam jak symulacja tych
taki sam jak symulacja tych
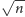 odwróceń. W trakcie
całego algorytmu takich większych faz musimy wykonać mniej więcej
odwróceń. W trakcie
całego algorytmu takich większych faz musimy wykonać mniej więcej
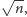 co daje łączną złożoność czasową
co daje łączną złożoność czasową
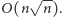
Na koniec warto dodać, że całe zadanie można rozwiązać także w czasie
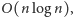 używając struktur danych opartych na drzewach
zrównoważonych. Jednak takie rozwiązanie nie było nigdy autorowi kącika do
szczęścia potrzebne.
używając struktur danych opartych na drzewach
zrównoważonych. Jednak takie rozwiązanie nie było nigdy autorowi kącika do
szczęścia potrzebne.