Informatyczny kącik olimpijski
Nurkowanie
Tym razem zajmiemy się zadaniem Nurkowanie z Obozu Naukowo-Treningowego im. Antoniego Kreczmara w 2007 roku.
Załóżmy dla uproszczenia, że nurkowie są ponumerowani od
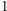 do
do
 tak, że czasy, jakie potrzebują oni na przepłynięcie szczeliny, spełniają
warunek
tak, że czasy, jakie potrzebują oni na przepłynięcie szczeliny, spełniają
warunek
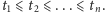 Sytuację daną w zadaniu opiszemy jako graf
Sytuację daną w zadaniu opiszemy jako graf
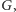 którego wierzchołki
którego wierzchołki
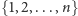 odpowiadają nurkom.
Nurkowie
odpowiadają nurkom.
Nurkowie
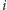 i
i
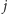 są połączeni w
są połączeni w
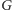 krawędzią wtedy i tylko
wtedy, gdy się lubią.
krawędzią wtedy i tylko
wtedy, gdy się lubią.
Zastanówmy się najpierw, kiedy problem nie ma rozwiązania. Każdy kolejny
krok schematu jest równoważny wybraniu dwóch wierzchołków
połączonych krawędzią w
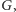 a następnie usunięciu z
a następnie usunięciu z
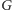 jednego
z nich, odpowiadającego nurkowi, który został po drugiej stronie szczeliny
i już nigdy stamtąd nie wróci. Jeśli więc
jednego
z nich, odpowiadającego nurkowi, który został po drugiej stronie szczeliny
i już nigdy stamtąd nie wróci. Jeśli więc
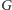 na początku nie jest
spójny, to na pewno przeprawa jest niewykonalna: po wykonaniu kursu liczba
składowych nie maleje, więc gdy już nie będzie można wykonać żadnego
kursu, pozostanie grupa co najmniej dwóch nurków, z których każdych
dwóch się nie lubi.
na początku nie jest
spójny, to na pewno przeprawa jest niewykonalna: po wykonaniu kursu liczba
składowych nie maleje, więc gdy już nie będzie można wykonać żadnego
kursu, pozostanie grupa co najmniej dwóch nurków, z których każdych
dwóch się nie lubi.
Załóżmy więc, że
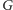 jest spójny. Okazuje się, że wtedy rozwiązanie
istnieje i każdy możliwy scenariusz przeprawy możemy skutecznie
modelować za pomocą drzewa ukorzenionego
jest spójny. Okazuje się, że wtedy rozwiązanie
istnieje i każdy możliwy scenariusz przeprawy możemy skutecznie
modelować za pomocą drzewa ukorzenionego
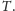 Ustanowimy nurka
Ustanowimy nurka
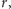 który uczestniczy w ostatniej turze przeprawy, korzeniem
naszego drzewa. Jeśli natomiast
który uczestniczy w ostatniej turze przeprawy, korzeniem
naszego drzewa. Jeśli natomiast
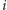 i
i
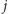 płyną razem, po czym
płyną razem, po czym
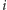 wraca, to
wraca, to
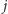 zostanie synem
zostanie synem
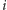 w
w
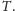 Jest jasne, że
wykonywanie scenariusza przeprawy odpowiada ucinaniu liści naszego drzewa.
Podobnie, mając dowolne ukorzenione drzewo rozpinające
Jest jasne, że
wykonywanie scenariusza przeprawy odpowiada ucinaniu liści naszego drzewa.
Podobnie, mając dowolne ukorzenione drzewo rozpinające
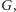 jesteśmy
w stanie na jego podstawie skonstruować scenariusz przeprawy –
wystarczy w dowolnej kolejności ucinać liście. Przypiszmy krawędziom
drzewa
jesteśmy
w stanie na jego podstawie skonstruować scenariusz przeprawy –
wystarczy w dowolnej kolejności ucinać liście. Przypiszmy krawędziom
drzewa
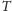 koszty czasowe odpowiadające kolejnym krokom. Jeśli
koszty czasowe odpowiadające kolejnym krokom. Jeśli
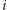 jest ojcem
jest ojcem
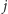 w
w
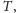 to krawędź między nimi ma koszt
to krawędź między nimi ma koszt
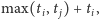 który, niestety, zależy nie tylko od wyboru nurków, ale
także od skierowania krawędzi między nimi. Kosztem
który, niestety, zależy nie tylko od wyboru nurków, ale
także od skierowania krawędzi między nimi. Kosztem
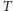 niech będzie
suma kosztów jego krawędzi pomniejszona o czas
niech będzie
suma kosztów jego krawędzi pomniejszona o czas
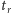 potrzebny
ostatniemu nurkowi na przeprawę (
potrzebny
ostatniemu nurkowi na przeprawę (
 nie musi wracać podczas
ostatniego kroku).
nie musi wracać podczas
ostatniego kroku).
Okazuje się, że przy tak ustalonych wagach da się uprościć problem, aby móc
zapomnieć o skierowaniu krawędzi i wyróżnionym korzeniu. Obliczmy
koszt drzewa
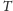 (
(
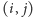 oznacza krawędź skierowaną od ojca
oznacza krawędź skierowaną od ojca
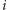 do syna
do syna
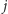 ):
):

Druga suma jest stała, więc koszt zależy tylko od pierwszego członu
wyrażenia! Wystarczy więc znaleźć minimalne drzewo rozpinające
grafu
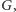 w którym krawędź
w którym krawędź
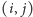 ma przypisany koszt
ma przypisany koszt
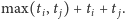
Ponieważ na wejściu mamy dane explicite dopełnienie grafu
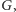 możemy
rozwiązać zadanie w czasie
możemy
rozwiązać zadanie w czasie
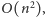 uruchamiając np. algorytm Prima.
Aby rozwiązać zadanie szybciej, zastosujemy podejście podobne jak
w algorytmie Borůvki. Przypomnijmy, że w algorytmie tym utrzymujemy las
rozpinający
uruchamiając np. algorytm Prima.
Aby rozwiązać zadanie szybciej, zastosujemy podejście podobne jak
w algorytmie Borůvki. Przypomnijmy, że w algorytmie tym utrzymujemy las
rozpinający
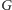 i wykonujemy
i wykonujemy
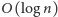 faz; w każdej fazie
działania dodajemy do konstruowanego rozwiązania najtańszą krawędź
wychodzącą z każdej dotychczasowej składowej lasu (rozstrzygając remisy
w dowolny uporządkowany sposób).
faz; w każdej fazie
działania dodajemy do konstruowanego rozwiązania najtańszą krawędź
wychodzącą z każdej dotychczasowej składowej lasu (rozstrzygając remisy
w dowolny uporządkowany sposób).
Pokażemy, jak zrealizować jedną fazę algorytmu Borůvki. Oznaczmy
przez
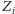 zbiór nurków, których nie lubi nurek
zbiór nurków, których nie lubi nurek
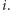 Niech
Niech
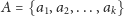 będzie zbiorem nurków dowolnej składowej
dotychczasowego rozwiązania (na początku każdy nurek stanowi osobną
składową). Niech
będzie zbiorem nurków dowolnej składowej
dotychczasowego rozwiązania (na początku każdy nurek stanowi osobną
składową). Niech
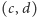 będzie szukaną najtańszą krawędzią wychodzącą
z
będzie szukaną najtańszą krawędzią wychodzącą
z
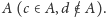 Jeśli
Jeśli
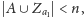 to niech
to niech
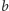 będzie
nurkiem o najmniejszym numerze nienależącym do
będzie
nurkiem o najmniejszym numerze nienależącym do
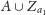 ; krawędź
; krawędź
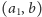 jest wtedy najtańszą krawędzią wychodzącą od nurka
jest wtedy najtańszą krawędzią wychodzącą od nurka
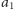 i kandydatem na najtańszą krawędź z
i kandydatem na najtańszą krawędź z
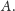 Wartość
Wartość
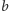 możemy znaleźć w czasie
możemy znaleźć w czasie
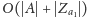 przy założeniu, że
zbiory reprezentujemy jako uporządkowane listy.
przy założeniu, że
zbiory reprezentujemy jako uporządkowane listy.
Pokażemy, jak to jeszcze usprawnić. Niech

Jeśli
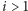 i krawędź
i krawędź
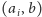 jest najtańszą krawędzią
wychodzącą z
jest najtańszą krawędzią
wychodzącą z
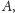 to
to
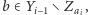 w przeciwnym razie
w przeciwnym razie
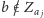 dla pewnego
dla pewnego
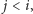 a krawędź
a krawędź
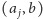 byłaby
tańsza. Wobec tego zarówno sprawdzenie każdego sensownego kandydata
byłaby
tańsza. Wobec tego zarówno sprawdzenie każdego sensownego kandydata
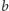 dla nurka
dla nurka
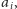 jak i obliczenie zbioru
jak i obliczenie zbioru
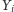 wykonujemy
w czasie
wykonujemy
w czasie
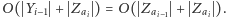 Sumując koszty dla
każdego wierzchołka składowej i dla każdej składowej, otrzymujemy
sumaryczny koszt jednej fazy algorytmu:
Sumując koszty dla
każdego wierzchołka składowej i dla każdej składowej, otrzymujemy
sumaryczny koszt jednej fazy algorytmu:

Złożoność czasowa całego rozwiązania wynosi zatem