Prostokąt arytmetyczny
W tym artykule omówimy zadanie Prostokąt arytmetyczny z Akademickich Mistrzostw Polski w Programowaniu Zespołowym 2011.
Jednak zanim to zrobimy, zastanowimy się nad dwoma pozornie niezwiązanymi problemami.

Rys. 1
Problem 1. Dany jest
 -elementowy ciąg
liczb całkowitych
-elementowy ciąg
liczb całkowitych
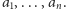 Chcielibyśmy dla każdego elementu
ciągu wyznaczyć najbliższy mniejszy od niego element położony na lewo
od niego. Formalnie, dla każdego
Chcielibyśmy dla każdego elementu
ciągu wyznaczyć najbliższy mniejszy od niego element położony na lewo
od niego. Formalnie, dla każdego
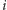 szukamy największego takiego
szukamy największego takiego
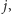
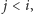 że
że
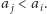 Aby ta wartość była zawsze
zdefiniowana, dokładamy sztuczny element
Aby ta wartość była zawsze
zdefiniowana, dokładamy sztuczny element
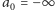 (patrz Rys. 1).
(patrz Rys. 1).
Najprostszy algorytm rozwiązujący Problem 1 działa w czasie
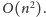 Używając
sprytnych struktur danych (zrównoważone drzewa binarne), można
otrzymać rozwiązanie działające w czasie
Używając
sprytnych struktur danych (zrównoważone drzewa binarne), można
otrzymać rozwiązanie działające w czasie
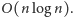 Podany problem
można jednak rozwiązać prosto i liniowo, jeśli tylko pójdzie się
za strzałkami.
Podany problem
można jednak rozwiązać prosto i liniowo, jeśli tylko pójdzie się
za strzałkami.

Rys. 2
Idea takiego rozwiązania jest jasna: będziemy przypisywać strzałki kolejnym
elementom, od lewej do prawej. Dla danego
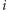 zaczynamy od sprawdzenia,
czy
zaczynamy od sprawdzenia,
czy
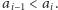 Jeśli tak, to wiemy, że strzałka z
Jeśli tak, to wiemy, że strzałka z
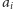 prowadzi do
prowadzi do
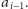 A jeśli nie, to idziemy do pierwszego elementu mniejszego niż
A jeśli nie, to idziemy do pierwszego elementu mniejszego niż
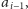 czyli dokładnie wzdłuż strzałki z
czyli dokładnie wzdłuż strzałki z
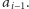 Kontynuujemy
to postępowanie aż do momentu, gdy znajdziemy element mniejszy
niż
Kontynuujemy
to postępowanie aż do momentu, gdy znajdziemy element mniejszy
niż
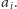 Przykładowo, rysunek 2 ilustruje wyznaczanie strzałki
wychodzącej z trójki.
Przykładowo, rysunek 2 ilustruje wyznaczanie strzałki
wychodzącej z trójki.

Rys. 3

Rys. 4
Aby uzasadnić, że ten algorytm jest liniowy, wystarczy pokazać, że wzdłuż
każdej strzałki przejdziemy co najwyżej raz. Faktycznie, jeśli przy
wyznaczaniu strzałki dla
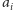 przechodzimy wzdłuż strzałki wychodzącej
z pewnego
przechodzimy wzdłuż strzałki wychodzącej
z pewnego
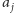 (
(
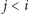 ), to wiemy, że
), to wiemy, że
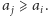 To oznacza,
że każda strzałka wychodząca z elementów
To oznacza,
że każda strzałka wychodząca z elementów
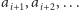 prowadzi
albo do
prowadzi
albo do
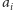 lub elementu położonego na prawo od
lub elementu położonego na prawo od
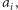 albo do
jakiegoś elementu mniejszego niż
albo do
jakiegoś elementu mniejszego niż
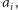 a zatem położonego na lewo od
a zatem położonego na lewo od
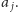 Strzałkę wychodzącą z
Strzałkę wychodzącą z
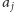 wykorzystamy zatem dokładnie raz,
co chcieliśmy wykazać.
wykorzystamy zatem dokładnie raz,
co chcieliśmy wykazać.
Problem 2. Mamy daną tablicę rozmiaru
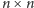 wypełnioną zerami
i jedynkami. Należy znaleźć prostokątny fragment tej tablicy wypełniony
samymi jedynkami o jak największej powierzchni (patrz Rys. 3).
wypełnioną zerami
i jedynkami. Należy znaleźć prostokątny fragment tej tablicy wypełniony
samymi jedynkami o jak największej powierzchni (patrz Rys. 3).
Ten problem pojawił się na IX Olimpiadzie Informatycznej jako zadanie Działka.
Wszystkich prostokątów w takiej tablicy jest rzędu
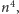 więc
problem trzeba rozwiązywać jakoś sprytniej. Znana jest cała gama
rozwiązań o złożoności czasowej
więc
problem trzeba rozwiązywać jakoś sprytniej. Znana jest cała gama
rozwiązań o złożoności czasowej
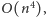
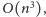 a nawet
a nawet
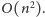 Pokażemy tu dosyć proste rozwiązanie o optymalnej
złożoności
Pokażemy tu dosyć proste rozwiązanie o optymalnej
złożoności
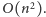 Zacznijmy od wyznaczenia dla każdego pola
Zacznijmy od wyznaczenia dla każdego pola
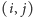 tablicy liczby kolejnych pól wypełnionych jedynkami położonych
w dół od tego pola, wliczając samo pole
tablicy liczby kolejnych pól wypełnionych jedynkami położonych
w dół od tego pola, wliczając samo pole
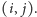 Oznaczmy tę
wartość przez
Oznaczmy tę
wartość przez
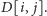 Takie wartości łatwo wyznaczamy w czasie
Takie wartości łatwo wyznaczamy w czasie
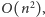 idąc od dołu do góry tablicy (Rys. 4). Zauważmy, że
idąc od dołu do góry tablicy (Rys. 4). Zauważmy, że
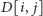 jest niezerowe tylko wtedy, gdy oryginalna tablica w polu
jest niezerowe tylko wtedy, gdy oryginalna tablica w polu
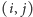 miała jedynkę.
miała jedynkę.
Teraz przychodzi kluczowe spostrzeżenie. Otóż poszukiwany prostokąt możemy
skonstruować tak: bierzemy jakieś pole
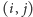 i wyznaczamy prostokąt
zawierający to pole w górnym wierszu, o wysokości
i wyznaczamy prostokąt
zawierający to pole w górnym wierszu, o wysokości
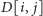 i sięgający
w prawo i w lewo tak daleko, jak tylko się da. Faktycznie, wynikowy prostokąt
nie może być rozszerzony w dół (ani w żadną inną stronę), więc musi być
opisanej postaci dla pewnego pola
i sięgający
w prawo i w lewo tak daleko, jak tylko się da. Faktycznie, wynikowy prostokąt
nie może być rozszerzony w dół (ani w żadną inną stronę), więc musi być
opisanej postaci dla pewnego pola
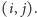 Przykładowo, na rysunkach
3 i 4 pole
Przykładowo, na rysunkach
3 i 4 pole
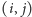 wynikowego prostokąta (kwadratu) o powierzchni 9 to
jego prawy górny róg.
wynikowego prostokąta (kwadratu) o powierzchni 9 to
jego prawy górny róg.
Dla każdego pola
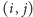 o niezerowym
o niezerowym
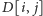 szukamy zatem
najbliższych pól w tym samym wierszu, dla których wartości
szukamy zatem
najbliższych pól w tym samym wierszu, dla których wartości
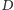 są
mniejsze niż
są
mniejsze niż
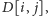 czyli takich indeksów
czyli takich indeksów
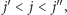 że
że
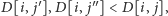
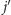 jest maksymalne, a
jest maksymalne, a
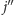 –
minimalne. Wówczas wynikiem jest maksimum z iloczynów postaci
–
minimalne. Wówczas wynikiem jest maksimum z iloczynów postaci
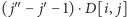 dla wszystkich pól
dla wszystkich pól
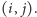 Zauważmy jednak,
że jest to dokładnie zastosowanie Problemu 1 do
Zauważmy jednak,
że jest to dokładnie zastosowanie Problemu 1 do
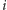 -tego wiersza
tablicy
-tego wiersza
tablicy
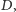 tyle że raz od lewej do prawej (wyznaczanie
tyle że raz od lewej do prawej (wyznaczanie
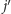 ),
a raz od prawej do lewej (wyznaczanie
),
a raz od prawej do lewej (wyznaczanie
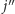 ). Wystarczy otoczyć tablicę
). Wystarczy otoczyć tablicę
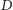 obwódką z polami zawierającymi
obwódką z polami zawierającymi
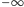 i możemy już
zastosować poprzedni algorytm, wiersz po wierszu. Dostajemy żądany czas
i możemy już
zastosować poprzedni algorytm, wiersz po wierszu. Dostajemy żądany czas

Rys. 5
Przyszła wreszcie pora, aby sformułować wspomniane na wstępie zadanie o prostokącie arytmetycznym.
Problem 3. Znów mamy daną tablicę rozmiaru
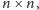 tym razem
mogą się w niej znajdować dowolne nieujemne liczby całkowite. Szukamy
w niej prostokąta arytmetycznego o maksymalnej powierzchni, przy czym
prostokąt arytmetyczny to prostokąt, w którym liczby w każdym wierszu
oraz w każdej kolumnie tworzą ciąg arytmetyczny (patrz Rys. 5).
tym razem
mogą się w niej znajdować dowolne nieujemne liczby całkowite. Szukamy
w niej prostokąta arytmetycznego o maksymalnej powierzchni, przy czym
prostokąt arytmetyczny to prostokąt, w którym liczby w każdym wierszu
oraz w każdej kolumnie tworzą ciąg arytmetyczny (patrz Rys. 5).
Na początek zajmijmy się prostokątami o wysokości 1. Widzimy, że
każdy wiersz tablicy możemy podzielić na maksymalne ciągi arytmetyczne,
z których każdy ma długość co najmniej dwa i każde dwa kolejne ciągi
mają dokładnie jeden element wspólny. Przykładowo, dolny wiersz tablicy
z rysunku 5 dzielimy na ciągi
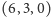 i
i
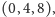 a górny na ciągi
a górny na ciągi
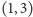 i
i
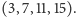 Korzystając z takiego przedstawienia,
w czasie
Korzystając z takiego przedstawienia,
w czasie
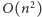 łatwo znajdziemy najdłuższy prostokąt arytmetyczny
o wysokości 1. Podobnie rozpatrujemy prostokąty o długości 1, wysokości 2
(jak?) i długości 2.
łatwo znajdziemy najdłuższy prostokąt arytmetyczny
o wysokości 1. Podobnie rozpatrujemy prostokąty o długości 1, wysokości 2
(jak?) i długości 2.

Rys. 6
Odtąd interesować nas będą tylko prostokąty, których każdy bok ma długość co najmniej 3. Znajdowanie takich prostokątów sprowadzimy do zadania Działka.
Zaznaczmy mianowicie kółkiem każdy taki element tablicy, że
kwadrat o boku 3 zawierający ten element w środku jest prostokątem
arytmetycznym (Rys. 6). Okazuje się, że prostokąt o obu wymiarach
nie mniejszych niż 3 jest arytmetyczny wtedy i tylko wtedy, gdy wszystkie
zawarte w nim elementy tablicy (poza, ewentualnie, jego wewnętrzną obwódką
o szerokości 1) są zaznaczone kółkami. Rzeczywiście, jeśli prostokąt
jest arytmetyczny, to każdy jego podprostokąt jest arytmetyczny, więc
w szczególności wszystkie kwadraty o boku 3, zawarte w tym prostokącie, są
arytmetyczne. A w drugą stronę, jeśli mamy dwa sąsiednie elementy tablicy
zaznaczone kółkami, to ciągi arytmetyczne w otaczających je kwadratach
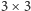 sklejają się w dłuższe ciągi arytmetyczne dokładnie tak,
jak trzeba.
sklejają się w dłuższe ciągi arytmetyczne dokładnie tak,
jak trzeba.

Podsumowując
Wąskie prostokąty arytmetyczne rozpatrzyliśmy osobno, a problem szukania
odpowiednio grubego prostokąta arytmetycznego o maksymalnej powierzchni
sprowadziliśmy do poszukiwania maksymalnych prostokątów złożonych
wyłącznie z wyróżnionych pól, czyli dokładnie do Problemu 2. Całe
rozwiązanie działa w optymalnym czasie
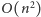 i jest, w sumie,
całkiem sprytne.
i jest, w sumie,
całkiem sprytne.
Na koniec ciekawa własność prostokątów arytmetycznych, która może zainteresować także nieinformatyków: prostokąt o wysokości co najmniej 2 jest arytmetyczny wtedy i tylko wtedy, gdy liczby w każdej jego kolumnie oraz w dowolnych dwóch jego wierszach tworzą ciągi arytmetyczne. Dodajmy, że ta własność nie zachodzi, jeśli wymagamy tylko, aby jeden wiersz prostokąta stanowił ciąg arytmetyczny.