Informatyczny kącik olimpijski
Monety
W tym miesiącu opiszemy zadanie Monety, które pojawiło się na Potyczkach Algorytmicznych w roku 2010.
Zadanie. Dany jest ciąg
 rzutów monetą. Należy sprawdzić,
jaka jest najdłuższa seria kolejnych rzutów, w której wypadło dokładnie
rzutów monetą. Należy sprawdzić,
jaka jest najdłuższa seria kolejnych rzutów, w której wypadło dokładnie
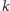 razy więcej orłów niż reszek. Dla przykładu, w ciągu
razy więcej orłów niż reszek. Dla przykładu, w ciągu

serie od piątego do dwunastego, jak również od szóstego do trzynastego
rzutu zawierają dokładnie 6 orłów i 2 reszki. Zatem
dla
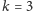 odpowiedzią jest 8, gdyż nie istnieje żadna dłuższa seria
zawierająca dokładnie 3 razy więcej orłów niż reszek.
odpowiedzią jest 8, gdyż nie istnieje żadna dłuższa seria
zawierająca dokładnie 3 razy więcej orłów niż reszek.
Uprośćmy na chwilę nasze zadanie i powiedzmy, że chcemy znaleźć
najdłuższą serię spełniającą warunki zadania, która zawiera pierwszy rzut.
Użyjemy dwóch zmiennych
 i
i
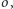 oznaczających liczby reszek
i orłów, które wypadły do tej pory. Za każdym razem, kiedy po rzucie
wystąpi
oznaczających liczby reszek
i orłów, które wypadły do tej pory. Za każdym razem, kiedy po rzucie
wystąpi
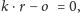 będzie to oznaczało, że znaleźliśmy dłuższą
serię. Zauważmy jednak, że nie potrzebujemy aż dwóch zmiennych:
nie interesuje nas dokładna liczba orłów i reszek, a jedynie ich wzajemne
zbilansowanie. Możemy więc trzymać jeden licznik
będzie to oznaczało, że znaleźliśmy dłuższą
serię. Zauważmy jednak, że nie potrzebujemy aż dwóch zmiennych:
nie interesuje nas dokładna liczba orłów i reszek, a jedynie ich wzajemne
zbilansowanie. Możemy więc trzymać jeden licznik
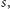 który po
każdym rzucie będziemy uaktualniali następująco: wyrzucenie reszki
zwiększa
który po
każdym rzucie będziemy uaktualniali następująco: wyrzucenie reszki
zwiększa
 o
o
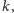 natomiast wyrzucenie orła zmniejsza
natomiast wyrzucenie orła zmniejsza
 o
o
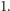 Oznaczmy przez
Oznaczmy przez
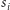 wartość licznika po
wartość licznika po
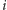 -tym rzucie
(przyjmujemy też
-tym rzucie
(przyjmujemy też
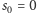 ). Teraz każde
). Teraz każde
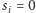 odpowiada
poprawnej serii kończącej się
odpowiada
poprawnej serii kończącej się
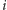 -tym rzutem.
-tym rzutem.
A co w ogólnym przypadku? Zastanówmy się, jaki warunek musi być
spełniony, aby pewna seria spełniająca warunki zadania kończyła się
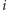 -tym rzutem monetą. Łatwo przekonać się, że jest tak wtedy, gdy
istnieje taki rzut
-tym rzutem monetą. Łatwo przekonać się, że jest tak wtedy, gdy
istnieje taki rzut
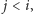 że wartość licznika po
że wartość licznika po
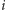 -tym rzucie jest
taka sama jak po
-tym rzucie jest
taka sama jak po
 -tym rzucie (
-tym rzucie (
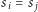 ) – wtedy rzuty od
) – wtedy rzuty od
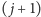 -ego do
-ego do
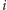 -tego tworzą poprawną serię. Chcielibyśmy zatem
dla danego
-tego tworzą poprawną serię. Chcielibyśmy zatem
dla danego
 szybko stwierdzać, jaki jest (o ile istnieje) najmniejszy
numer rzutu
szybko stwierdzać, jaki jest (o ile istnieje) najmniejszy
numer rzutu
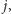 dla którego
dla którego
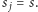 Skorzystamy w tym celu
z drzewa wyszukiwań binarnych, w którym dla klucza
Skorzystamy w tym celu
z drzewa wyszukiwań binarnych, w którym dla klucza
 będziemy
trzymać odpowiadający mu numer rzutu. Teraz po
będziemy
trzymać odpowiadający mu numer rzutu. Teraz po
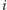 -tym rzucie, jeśli
klucz
-tym rzucie, jeśli
klucz
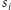 występuje w drzewie z wartością
występuje w drzewie z wartością
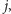 to zgłaszamy
znalezienie serii o długości
to zgłaszamy
znalezienie serii o długości
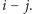 W przeciwnym przypadku
uaktualniamy drzewo, wstawiając do niego klucz
W przeciwnym przypadku
uaktualniamy drzewo, wstawiając do niego klucz
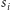 z wartością
z wartością
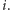 Zauważmy, że jeśli w drzewie istniał już klucz
Zauważmy, że jeśli w drzewie istniał już klucz
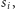 to
nie musieliśmy go uaktualniać, gdyż interesuje nas jedynie najmniejszy
numer rzutu odpowiadający temu kluczowi. Każda operacja na drzewie
zajmuje czas
to
nie musieliśmy go uaktualniać, gdyż interesuje nas jedynie najmniejszy
numer rzutu odpowiadający temu kluczowi. Każda operacja na drzewie
zajmuje czas
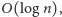 zatem całe rozwiązanie działa w czasie
zatem całe rozwiązanie działa w czasie
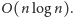
Czytelnicy, którzy słyszeli o tablicach haszujących, mogą powiedzieć, że
bez kłopotu uzyskalibyśmy rozwiązanie działające w oczekiwanym
czasie
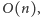 gdybyśmy zamiast drzewa wyszukiwań binarnych
użyli właśnie tablicy haszującej. To prawda, ale okazuje się, że można
jeszcze lepiej – wykorzystując specyfikę naszego zadania, można
zaprojektować „tablicę haszującą”, która da nam rozwiązanie
gdybyśmy zamiast drzewa wyszukiwań binarnych
użyli właśnie tablicy haszującej. To prawda, ale okazuje się, że można
jeszcze lepiej – wykorzystując specyfikę naszego zadania, można
zaprojektować „tablicę haszującą”, która da nam rozwiązanie
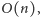 i to
w pesymistycznym przypadku!
i to
w pesymistycznym przypadku!
Zamiast drzewa będziemy mieli tablicę
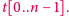 Odwołania do klucza
Odwołania do klucza
 będą realizowane przez komórkę
będą realizowane przez komórkę
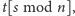 w której będziemy
trzymać listę par postaci (klucz
w której będziemy
trzymać listę par postaci (klucz
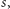 numer rzutu). Innymi słowy, po
numer rzutu). Innymi słowy, po
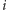 -tym rzucie sprawdzamy, czy na liście
-tym rzucie sprawdzamy, czy na liście
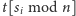 znajduje się
para
znajduje się
para
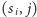 dla pewnego
dla pewnego
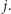 Jeśli tak, to zgłaszamy znalezienie serii
o długości
Jeśli tak, to zgłaszamy znalezienie serii
o długości
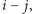 a w przeciwnym przypadku uaktualniamy listę
a w przeciwnym przypadku uaktualniamy listę
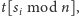 wstawiając do niej nową parę
wstawiając do niej nową parę
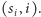
I teraz czas na kluczową obserwację. Załóżmy, że nastąpił drugi z powyższych
przypadków. To oznacza, że na liście
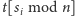 mogą znajdować się
tylko pary
mogą znajdować się
tylko pary
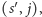 gdzie
gdzie
 dla
dla
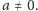 Zauważmy
jednak, że ilekroć nasz licznik osiągnął pewną wartość
Zauważmy
jednak, że ilekroć nasz licznik osiągnął pewną wartość
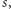 to
w przyszłości już nigdy nie będzie równy
to
w przyszłości już nigdy nie będzie równy
 lub mniejszy,
ponieważ po każdym rzucie możemy go zmniejszyć co najwyżej o
lub mniejszy,
ponieważ po każdym rzucie możemy go zmniejszyć co najwyżej o
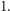 Zatem na liście nie ma żadnej pary dla
Zatem na liście nie ma żadnej pary dla
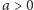 (bo
wtedy byłoby
(bo
wtedy byłoby
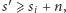 co przeczy temu, że aktualna wartość
licznika to
co przeczy temu, że aktualna wartość
licznika to
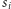 ). Co więcej, skoro pary, które mogą pojawić się
na liście, spełniają
). Co więcej, skoro pary, które mogą pojawić się
na liście, spełniają
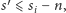 to sytuacja, w której licznik byłby
równy
to sytuacja, w której licznik byłby
równy
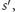 nigdy już nie wystąpi. Tak więc przed dodaniem pary
nigdy już nie wystąpi. Tak więc przed dodaniem pary
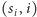 do listy
do listy
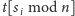 możemy z niej usunąć wszystkie
występujące na niej pary. Widać zatem, że na żadnej liście nie będzie nigdy
więcej niż jednej pary – stąd czas wyszukiwania na liście faktycznie
będzie stały.
możemy z niej usunąć wszystkie
występujące na niej pary. Widać zatem, że na żadnej liście nie będzie nigdy
więcej niż jednej pary – stąd czas wyszukiwania na liście faktycznie
będzie stały.
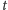 to po prostu tablica z haszowaniem modularnym,
stosująca metodę łańcuchową do rozwiązywania kolizji. Zauważmy, że
używamy tutaj matematycznej definicji operacji modulo:
to po prostu tablica z haszowaniem modularnym,
stosująca metodę łańcuchową do rozwiązywania kolizji. Zauważmy, że
używamy tutaj matematycznej definicji operacji modulo:
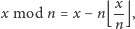
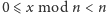 nawet dla ujemnych wartości
nawet dla ujemnych wartości
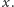 Nie jest
to jednak definicja powszechnie obowiązująca w popularnych językach
programowania.
Nie jest
to jednak definicja powszechnie obowiązująca w popularnych językach
programowania.