Pierwsze rozwiązanie, które powinno przyjść nam do głowy, wykorzystuje obserwację, że każdy szukany prostokąt jest jednoznacznie określony przez jego dwa przeciwległe wierzchołki. Możemy więc dla każdej pary danych punktów (lewy dolny, prawy górny) sprawdzić, czy do zbioru należą dwa pozostałe wierzchołki. Jeśli do sprawdzania przynależności do zbioru wykorzystamy tablicę haszującą, takie rozwiązanie będzie działało w czasie

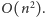
Może się wydawać, że sporo czasu w powyższym rozwiązaniu tracimy na sprawdzaniu „złych” par – przekątnych, dla których pozostałe dwa punkty nie istnieją. Niestety, prosty przykład  punktów ustawionych w „dwuszereg” pokazuje, że wynik może być rzędu 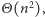 zatem żaden algorytm zliczający prostokąty pojedynczo nie może być istotnie lepszy od powyższego.

Jak zatem znaleźć lepsze rozwiązanie? Zauważmy na początek, że możemy przenumerować współrzędne na wejściu tak, aby wszystkie były naturalne i nie większe niż 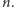 Nie interesują nas bowiem długości boków czy pola prostokątów, tylko ich liczba. Podzielmy punkty na pionowe bloki, tj. ze względu na współrzędną 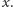 Bloki natomiast podzielmy na dwie kategorie – małe, czyli te, które zawierają co najwyżej 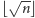 punktów, i duże, czyli pozostałe.

Zapomnijmy na moment o dużych blokach. Powiemy, że współrzędna 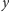 należy do bloku, jeśli w bloku znajduje się punkt o drugiej współrzędnej równej 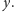 Będziemy iterować po możliwych położeniach dolnego boku prostokąta, od góry do dołu. Załóżmy, że dolny bok prostokąta ma drugą współrzędną równą 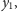 i rozważmy te bloki, do których należy punkt o takiej współrzędnej – punkty w pozostałych blokach nie mają szans należeć do takiego prostokąta. Ignorujemy także wszystkie punkty o drugich współrzędnych nie większych niż 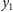 – te także nie mają wpływu na wynik. Teraz wystarczy policzyć, ile jest poziomych odcinków o obu końcach wśród punktów, które nam pozostały – jako że każdy blok zawiera 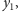 każdy taki odcinek odpowiada jednemu prostokątowi. Ten krok można wykonać łatwo, przechodząc po wszystkich punktach, które nam pozostały (w dowolnej kolejności, np. od lewej do prawej), przy okazji zliczając w tablicy (współrzędne są małe!), ile razy dana rzędna już wystąpiła, i aktualizując wynik.

Załóżmy, że wielkości małych bloków to 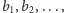 przy czym 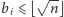 i 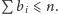  Przy uważnej implementacji algorytmu małych bloków wykonamy w nim liczbę operacji co najwyżej rzędu 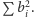 Faktycznie, wybrana współrzędna 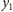 będzie należała do 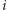-tego bloku 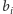 razy, i wówczas w fazie przeglądania każdy punkt tego bloku odwiedzimy co najwyżej raz. Wykażemy, że 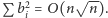 Spróbujmy znaleźć „najgorszy możliwy” ciąg 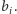 Jeśli dla pewnych różnych 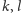 mamy 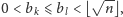 to zmniejszając 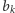 o 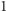 i zwiększając 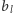 o 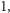 nie zmieniamy 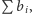 a jednocześnie zwiększamy 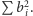 Jest to konsekwencja wypukłości funkcji kwadratowej. Powtarzając tę operację dostatecznie dużo razy, otrzymamy wszystkie liczby 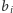 – być może z wyjątkiem jednej – równe 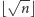 lub 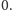 Tych niezerowych będzie co najwyżej 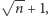 ponieważ 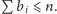 Ostatecznie, dostajemy

Pozostało nam zająć się dużymi blokami. Dla dowolnego bloku 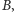 łatwo policzyć w czasie 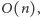 ile jest prostokątów, które mają dwa punkty w tym bloku – jeśli dla każdego pozostałego bloku 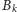 znamy liczbę współrzędnych 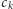 wspólnych dla 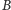 i 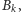 to szukaną przez nas liczbą jest 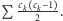 Ponieważ tę sumę dodamy do wyniku dla każdego dużego bloku, więc prostokąty o wszystkich punktach w dużych blokach policzymy dwukrotnie 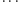 To jednak nie jest duży problem – aby się z nim uporać, wystarczy dla każdego dużego bloku zawrzeć w sumie wszystkie małe bloki i tylko te duże, które znajdują się na lewo od niego. Na szczęście, duże bloki są wystarczająco liczne, aby nie mogło ich być więcej niż 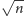 – a więc ta faza działa także w czasie 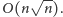W powyższych rozważaniach zapomnieliśmy o kosztach związanych z sortowaniem i przenumerowaniem wejściowych współrzędnych. 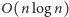Te nie powinny wynieść jednak więcej niż  operacji, więc są znikome w porównaniu z kosztem faz zliczających. Całe rozwiązanie działa więc w czasie 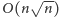 i pamięci

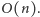
Zainteresowanemu Czytelnikowi polecamy zastanowienie się, co by było, gdybyśmy chcieli, zamiast prostokątów, zliczać kwadraty. Czy umiemy to zrobić szybciej, czy potrzebujemy bardziej skomplikowanych struktur danych? Tak sformułowane zadanie pojawiło się na Obozie Naukowo-Treningowym im. A. Kreczmara w 2010 roku pod tytułem Ogródek i można je rozwiązywać w serwisie main.edu.pl.