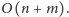Informatyczny kącik olimpijski
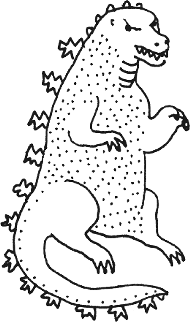
Godzilla
W tym miesiącu omówimy zadanie, które rozwiązywali uczestnicy Obozu Naukowo-Treningowego im. A. Kreczmara w 2009 r.
Zadanie 1. Sieć telewizji kablowej składa się z
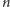 węzłów
i
węzłów
i
 jednokierunkowych połączeń. Do każdego węzła sieci jest
podłączony co najmniej jeden dom. Niektóre węzły są wyróżnione
i do nich bezpośrednio transmitowany jest program. W danym domu
można go oglądać, jeśli istnieje połączenie (niekoniecznie bezpośrednie)
od wyróżnionego węzła do węzła, do którego podłączony jest dom.
jednokierunkowych połączeń. Do każdego węzła sieci jest
podłączony co najmniej jeden dom. Niektóre węzły są wyróżnione
i do nich bezpośrednio transmitowany jest program. W danym domu
można go oglądać, jeśli istnieje połączenie (niekoniecznie bezpośrednie)
od wyróżnionego węzła do węzła, do którego podłączony jest dom.
Niestety, sieć jest narażona na ataki złośliwej Godzilli, która,
nie wiedzieć czemu, żywi się infrastrukturą telewizji kablowej. Co dzień
zjada ona jedno połączenie z sieci. Mając daną listę
 połączeń,
które kolejno zje Godzilla, należy wyznaczyć, ile minimalnie węzłów
należy oznaczyć jako wyróżnione każdego dnia, tak aby każdy dom
mógł odbierać program.
połączeń,
które kolejno zje Godzilla, należy wyznaczyć, ile minimalnie węzłów
należy oznaczyć jako wyróżnione każdego dnia, tak aby każdy dom
mógł odbierać program.
Sieć kablową możemy traktować jako graf skierowany
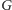 o
o
 wierzchołkach i
wierzchołkach i
 krawędziach. Aby znaleźć minimalny
zbiór wyróżnionych węzłów, wyznaczamy podział grafu
krawędziach. Aby znaleźć minimalny
zbiór wyróżnionych węzłów, wyznaczamy podział grafu
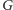 na
silnie spójne składowe. Silnie spójną składową nazwiemy początkową, jeśli
nie wchodzi do niej żadna krawędź (tzn. do żadnego wierzchołka tej
składowej nie wchodzi krawędź z wierzchołka spoza tej składowej).
Zauważmy, że w każdej początkowej składowej musimy wyróżnić
co najmniej jeden wierzchołek, aby dostarczyć program do wierzchołków tej
składowej. A ponieważ do każdej niepoczątkowej składowej istnieje
ścieżka ze składowej początkowej, więc taki zbiór wierzchołków
jest wystarczający.
na
silnie spójne składowe. Silnie spójną składową nazwiemy początkową, jeśli
nie wchodzi do niej żadna krawędź (tzn. do żadnego wierzchołka tej
składowej nie wchodzi krawędź z wierzchołka spoza tej składowej).
Zauważmy, że w każdej początkowej składowej musimy wyróżnić
co najmniej jeden wierzchołek, aby dostarczyć program do wierzchołków tej
składowej. A ponieważ do każdej niepoczątkowej składowej istnieje
ścieżka ze składowej początkowej, więc taki zbiór wierzchołków
jest wystarczający.
Znajdowanie podziału na silnie spójne składowe możemy zrealizować
dwukrotnym przejściem grafu w głąb w czasie
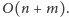 Jeśli
po każdym usunięciu krawędzi będziemy wyznaczali ten podział od nowa,
dostaniemy algorytm o koszcie czasowym
Jeśli
po każdym usunięciu krawędzi będziemy wyznaczali ten podział od nowa,
dostaniemy algorytm o koszcie czasowym
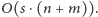
Chcielibyśmy umieć szybko uaktualniać strukturę składowych po usunięciu
krawędzi. Nie jest jednak jasne, jak to zrobić, gdyż po takiej operacji jedna
ze składowych może rozpaść się na mniejsze składowe i wydaje się, że
nie da się ich wyznaczyć szybciej niż w czasie liniowym względem rozmiaru
oryginalnej składowej. Zastosujemy więc pomysłową sztuczkę i odwrócimy
czas: zaczniemy od grafu, w którym usunięto wszystkie
 krawędzi,
i będziemy je dodawać do grafu w odwrotnej kolejności. Tym sposobem
pojedynczą operacją będzie połączenie kilku składowych w jedną, a to już
wygląda przyjaźniej.
krawędzi,
i będziemy je dodawać do grafu w odwrotnej kolejności. Tym sposobem
pojedynczą operacją będzie połączenie kilku składowych w jedną, a to już
wygląda przyjaźniej.
Niech
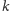 będzie aktualną liczbą początkowych składowych. Przez cały czas
będziemy utrzymywać podział zbioru wierzchołków grafu
będzie aktualną liczbą początkowych składowych. Przez cały czas
będziemy utrzymywać podział zbioru wierzchołków grafu

Zbiór
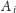 tworzą wierzchołki
tworzą wierzchołki
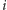 -tej początkowej składowej; do
zbioru
-tej początkowej składowej; do
zbioru
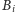 należą zaś wierzchołki, które są osiągalne z
należą zaś wierzchołki, które są osiągalne z
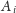 (jeśli
wierzchołek jest osiągalny z kilku początkowych składowych, to należy do
zbioru
(jeśli
wierzchołek jest osiągalny z kilku początkowych składowych, to należy do
zbioru
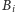 dla jednej z tych składowych).
dla jednej z tych składowych).
Zobaczmy, co się dzieje, gdy dodajemy do grafu nową krawędź
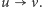 Jeśli
Jeśli
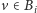 dla pewnego
dla pewnego
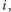 to dodanie tej krawędzi nie spowoduje
żadnych zmian w strukturze początkowych składowych, a więc nie musimy
nic robić.
to dodanie tej krawędzi nie spowoduje
żadnych zmian w strukturze początkowych składowych, a więc nie musimy
nic robić.
W przeciwnym przypadku
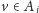 dla pewnego
dla pewnego
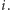 Będziemy
przeszukiwać graf transponowany
Będziemy
przeszukiwać graf transponowany
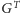 (czyli przechodzić krawędzie
grafu
(czyli przechodzić krawędzie
grafu
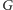 w odwrotnym kierunku), np. algorytmem DFS, począwszy
od wierzchołka
w odwrotnym kierunku), np. algorytmem DFS, począwszy
od wierzchołka
 Dla każdego napotkanego wierzchołka
Dla każdego napotkanego wierzchołka
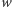 ze zbioru
ze zbioru
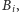 przenosimy go do zbioru
przenosimy go do zbioru
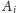 (wiemy, że
jest cykl
(wiemy, że
jest cykl
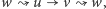 gdyż
gdyż
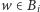 jest osiągalny z
jest osiągalny z
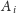 ).
Oczywiście, dla każdego napotkanego wierzchołka
).
Oczywiście, dla każdego napotkanego wierzchołka
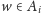 ucinamy
przeszukiwanie, gdyż gdy raz wejdziemy do
ucinamy
przeszukiwanie, gdyż gdy raz wejdziemy do
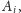 to już z niego
nie wyjdziemy.
to już z niego
nie wyjdziemy.
Jeśli zaś napotkamy wierzchołek
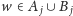 dla
dla
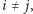 to znaczy,
że znaleźliśmy ścieżkę, która pokazuje, iż składowa
to znaczy,
że znaleźliśmy ścieżkę, która pokazuje, iż składowa
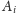 stała się
osiągalna ze składowej
stała się
osiągalna ze składowej
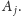 Zatem powiększamy
Zatem powiększamy
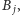 wykonując
wykonując
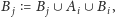 usuwamy zbiory
usuwamy zbiory
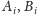 i kończymy
przeszukiwanie. Liczba początkowych składowych zmalała o jeden.
i kończymy
przeszukiwanie. Liczba początkowych składowych zmalała o jeden.
Oszacujmy złożoność czasową naszego algorytmu. Obliczenie podziału dla
początkowego grafu
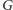 bez
bez
 zjedzonych krawędzi realizujemy
w czasie
zjedzonych krawędzi realizujemy
w czasie
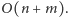 Podział ten będziemy przechowywać
w strukturze danych dla zbiorów rozłącznych (ang. find-union). Wtedy
każda operacja 1) zapytania, do którego ze zbiorów należy dany
wierzchołek i 2) złączenia zbiorów będzie miała „prawie stały” koszt
zamortyzowany – a dokładniej
Podział ten będziemy przechowywać
w strukturze danych dla zbiorów rozłącznych (ang. find-union). Wtedy
każda operacja 1) zapytania, do którego ze zbiorów należy dany
wierzchołek i 2) złączenia zbiorów będzie miała „prawie stały” koszt
zamortyzowany – a dokładniej
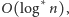 przy czym w praktyce
przy czym w praktyce
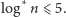 Dodatkowo, sumaryczny czas przeszukiwania grafu
Dodatkowo, sumaryczny czas przeszukiwania grafu
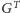 wynosi
wynosi
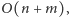 gdyż każdą krawędzią przechodzimy
co najwyżej raz.
gdyż każdą krawędzią przechodzimy
co najwyżej raz.
Zatem całkowity koszt czasowy to
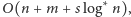 przy zużyciu
pamięci rzędu
przy zużyciu
pamięci rzędu