Jak złapać terrorystę?
Któż z nas nie bawił się jako dziecko w chowanego? Zabawa ta sprawia dzieciom wiele radości, mimo że z algorytmicznego punktu widzenia jest bardzo prosta. Jeżeli bowiem wszyscy ukrywający się czekają uczciwie w swoich kryjówkach, to zawsze uda się ich znaleźć – wystarczy, jeżeli szukający przejrzy wszystkie miejsca.
Sytuacja jednak komplikuje się, kiedy ukryte osoby mogą zmieniać swoje kryjówki w czasie poszukiwań. Okazuje się, że wtedy szala trudności przechyla się w drugą stronę. O ile w oryginalnym sformułowaniu wiele osób ukrywało się i wystarczyła jedna, aby je znaleźć, o tyle teraz do znalezienia nawet jednej osoby zwykle potrzeba wielu szukających.
Poszukiwania stają się jeszcze trudniejsze, jeżeli nie znamy ograniczenia na prędkość uciekiniera. Zapewne sytuacja ta jest dobrze znana rodzicom próbującym znaleźć swoje pociechy – dobrze wiedzą, że dzieci potrafią się poruszać z dowolną prędkością, niekoniecznie ograniczoną przez prędkość światła.
Problem. Spróbujmy sformalizować nasze zadanie. Zastanawiamy się nad kwestią przeszukiwania spójnego grafu nieskierowanego, np. reprezentującego budynek, w którym ukrywa się terrorysta. Nie wiemy, gdzie on jest, jak się będzie poruszał ani nawet jak szybko będzie w stanie to robić. Interesuje nas minimalna liczba policjantów potrzebnych do przeszukania grafu i złapania terrorysty bez względu na jego sposób poruszania się.
To zadanie ma wiele wersji, więc potrzebujemy uściślić pewne założenia. W naszym przypadku zakładamy, że terrorysta zostanie złapany, jeżeli w danym momencie spotka policjanta w tym samym wierzchołku bądź w tym samym punkcie krawędzi. Innymi słowy, stojąc w dowolnym wierzchołku, policjant widzi jedynie ten wierzchołek (bez krawędzi z niego wychodzących) i podobnie, stojąc w krawędzi, widzi tylko ten jej punkt, w którym sam się znajduje, a nie całą krawędź.
Szukana liczba policjantów jest parametrem grafu. Nazwijmy ją liczbą policyjną grafu.
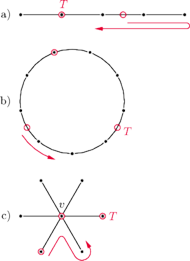
Rys. 1 Wyznaczanie liczby policyjnej a) ścieżki, b) cyklu, c) gwiazdy. Kolorowy punkt z literą
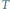 oznacza terrorystę, pozostałe punkty oznaczają policjantów. Kolorowe strzałki pokazują
strategię policjantów.
oznacza terrorystę, pozostałe punkty oznaczają policjantów. Kolorowe strzałki pokazują
strategię policjantów.
Rozpatrzmy kilka przykładów (patrz Rys. 1):
- Dla grafu będącego ścieżką liczba policyjna wynosi 1, bo wystarczy, że jedna osoba przejdzie graf od początku do końca.
- Dla cyklu potrzebne są już dwie osoby, bo jeżeli jeden policjant porusza się po cyklu, to terrorysta może np. zawsze ukrywać się w wierzchołku sąsiednim do tego, w którym jest policjant, i poruszać się tak samo, jak on. Dwóch policjantów już może przeszukać cykl – wystarczy, jeżeli jeden poczeka w pewnym wierzchołku, a drugi przejdzie cały cykl.
- Dla
gwiazdy (czyli grafu, w którym pewien wierzchołek
 jest
połączony ze wszystkimi pozostałymi, a każda krawędź jest
incydentna z
jest
połączony ze wszystkimi pozostałymi, a każda krawędź jest
incydentna z
 ) potrzeba dwóch przeszukujących, bo
w czasie, kiedy jeden odwiedza pewien wierzchołek różny
od
) potrzeba dwóch przeszukujących, bo
w czasie, kiedy jeden odwiedza pewien wierzchołek różny
od
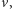 terrorysta może przemieszczać się dowolnie po
pozostałych
wierzchołkach (pod warunkiem, że wszystkich wierzchołków jest
co najmniej 4). Dwóch policjantów wystarczy, bo jeden może
stanąć w wierzchołku
terrorysta może przemieszczać się dowolnie po
pozostałych
wierzchołkach (pod warunkiem, że wszystkich wierzchołków jest
co najmniej 4). Dwóch policjantów wystarczy, bo jeden może
stanąć w wierzchołku
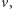 a drugi w tym czasie może
przejrzeć cały graf.
a drugi w tym czasie może
przejrzeć cały graf.
Pierwsze próby rozwiązania
Zastanówmy się nad jakimiś ograniczeniami na liczbę szukających.
Oczywiście, zawsze wystarczy
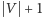 policjantów, gdzie
policjantów, gdzie
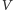 jest
zbiorem wierzchołków grafu, ponieważ możemy w każdym wierzchołku
postawić strażnika i jednym dodatkowym policjantem przeszukać
wszystkie krawędzie. Jest to jednak bardzo zgrubne ograniczenie, zwykle
liczba policyjna będzie znacznie mniejsza. Wiemy jednak dzięki niemu,
że rząd rozwiązania to
jest
zbiorem wierzchołków grafu, ponieważ możemy w każdym wierzchołku
postawić strażnika i jednym dodatkowym policjantem przeszukać
wszystkie krawędzie. Jest to jednak bardzo zgrubne ograniczenie, zwykle
liczba policyjna będzie znacznie mniejsza. Wiemy jednak dzięki niemu,
że rząd rozwiązania to
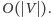 Możemy też dla danego grafu
Możemy też dla danego grafu
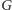 wykonywać pewne redukcje do mniejszych instancji zadania (choć
nie wszystkie zachowają dokładne rozwiązanie):
wykonywać pewne redukcje do mniejszych instancji zadania (choć
nie wszystkie zachowają dokładne rozwiązanie):
- Możemy z grafu usunąć każdy wierzchołek stopnia 2, łącząc przy tym incydentne z nim krawędzie w jedną.
- Możemy umieścić kilku (powiedzmy
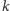 ) strażników
w pewnym podzbiorze wierzchołków, którego usunięcie
spowodowałoby rozspójnienie grafu (możemy np. wybrać
do tego punkty artykulacji). Następnie możemy znaleźć
rozwiązanie dla każdej z powstałych spójnych składowych
oddzielnie. Powiedzmy, że znalezione dla nich liczby policyjne
to
) strażników
w pewnym podzbiorze wierzchołków, którego usunięcie
spowodowałoby rozspójnienie grafu (możemy np. wybrać
do tego punkty artykulacji). Następnie możemy znaleźć
rozwiązanie dla każdej z powstałych spójnych składowych
oddzielnie. Powiedzmy, że znalezione dla nich liczby policyjne
to
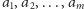 ; wtedy dostateczną (choć niekoniecznie
minimalną) liczbą jest
; wtedy dostateczną (choć niekoniecznie
minimalną) liczbą jest
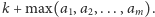 Odpowiada
to strategii, w której zespół
Odpowiada
to strategii, w której zespół
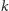 policjantów pilnuje
przejścia między otrzymanymi spójnymi składowymi, natomiast
zespół pozostałych przeszukuje po kolei wszystkie składowe.
policjantów pilnuje
przejścia między otrzymanymi spójnymi składowymi, natomiast
zespół pozostałych przeszukuje po kolei wszystkie składowe.
- Możemy z grafu usunąć wszystkie wierzchołki o stopniu 1
(incydentne z dokładnie jedną krawędzią – nazwijmy je liśćmi),
otrzymując graf
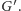 Jeżeli obliczymy liczbę policyjną
Jeżeli obliczymy liczbę policyjną
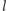 dla grafu
dla grafu
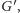 to do przeszukania oryginalnego
grafu
to do przeszukania oryginalnego
grafu
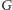 wystarczy
nam
wystarczy
nam
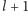 policjantów, ponieważ możemy przy pomocy
policjantów, ponieważ możemy przy pomocy
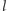 policjantów przeszukiwać podgraf
policjantów przeszukiwać podgraf
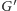 i dla
każdego liścia
i dla
każdego liścia
 całego grafu
całego grafu
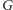 zatrzymać tych
zatrzymać tych
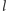 policjantów w momencie, kiedy jedyny
sąsiad
policjantów w momencie, kiedy jedyny
sąsiad
 liścia
liścia
 zostaje po raz ostatni odwiedzony
w strategii przeszukiwania
zostaje po raz ostatni odwiedzony
w strategii przeszukiwania
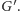 W tym momencie może
wkroczyć do akcji dodatkowy policjant, który przybiegnie do
W tym momencie może
wkroczyć do akcji dodatkowy policjant, który przybiegnie do
 i z niego przejdzie
do
i z niego przejdzie
do
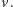 W ten sposób wierzchołek
W ten sposób wierzchołek
 oraz incydentna
z nim krawędź
oraz incydentna
z nim krawędź
 zostaną przeszukane i nigdy więcej
terrorysta nie będzie mógł się tam znaleźć.
zostaną przeszukane i nigdy więcej
terrorysta nie będzie mógł się tam znaleźć.
Niestety, powyższe redukcje (oprócz pierwszej) nie są dokładne, tzn. pozwalają jedynie na znalezienie pewnej dostatecznej liczby policjantów, ale niekoniecznie minimalnej.
Okazuje się, że problem wyznaczenia liczby policyjnej grafu jest NP-trudny.
Znaczy to, że ludzkość nie zna żadnego rozwiązania o wielomianowej
złożoności czasowej. Jednak w przypadku tego problemu nie jest nawet
jasne, w jaki sposób rozwiązać go w czasie wykładniczym lub nawet
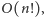 co dla większości NP-trudnych problemów jest oczywiste.
co dla większości NP-trudnych problemów jest oczywiste.
Postarajmy się więc znaleźć rozwiązanie działające w czasie wykładniczym.
Algorytm
Znamy już pewne sposoby ograniczania liczby policyjnej z góry. Żeby jednak móc analizować jej ograniczenia z dołu, potrzebujemy jakiegoś opisu wszystkich możliwych rozwiązań. Do skonstruowania tego opisu będzie nam pomocny następujący
Fakt 1. Liczba policyjna grafu nie zmienia się przy przyjęciu ograniczenia, że policjanci poruszają się po kolei, tzn. w każdym kroku jeden z nich przesuwa się do sąsiedniego wierzchołka.
Dzięki temu stwierdzeniu możemy podzielić cały czas przeszukiwania na dyskretne momenty. To pozwala nam w pewien sposób opisać i usystematyzować możliwe strategie jako sekwencje dyskretnych ruchów policjantów.
Jeżeli znalibyśmy jeszcze górne ograniczenia na czas przeszukiwania w takiej strategii, to moglibyśmy już podać pewien „brutalny” algorytm przeszukujący wszystkie możliwe sekwencje ruchów. Złożoność takiego podejścia byłaby trudna do oszacowania, jednak prawdopodobnie istotnie przekraczałaby złożoność wykładniczą.
Zadanie upraszcza się, jeżeli spojrzymy na nie z innej strony. Otóż zamiast zastanawiać się nad różnymi strategiami, przyjrzyjmy się możliwym kolejnościom przeszukiwania krawędzi.
Jeżeli założymy, że w każdym ruchu pewien policjant przechodzi z pewnego wierzchołka do sąsiedniego, to w naturalny sposób pojawią się pojęcia krawędzi skażonej i krawędzi czystej, czyli odpowiednio takiej, w której może być terrorysta, i takiej, w której na pewno terrorysty w danym momencie nie ma.
Teraz będzie nam potrzebny jeszcze jeden, nietrywialny fakt.
Fakt 2. Istnieje optymalna strategia monotoniczna, tzn. taka, w której zbiór krawędzi czystych rośnie (czyli jeśli jakaś krawędź jest czysta w danym momencie, to już do końca przeszukiwania taka będzie).
Tak więc, zamiast badać, czy dana strategia przeszukuje wszystkie krawędzie, pomyślmy nad dowolną sekwencją oczyszczania krawędzi i obliczmy, ilu potrzeba policjantów, aby ją zrealizować. Jeżeli następnie zbadamy to dla wszystkich możliwych kolejności przeszukiwania krawędzi, to minimum z otrzymanych wyników będzie równe liczbie policyjnej grafu.
Jak dla danej kolejności przeszukiwania krawędzi wyznaczyć liczbę potrzebnych policjantów? Rozważmy zbiory czystych krawędzi w kolejnych momentach. Zauważmy, że do blokowania czystego podzbioru krawędzi potrzeba dokładnie tylu policjantów, ile jest w grafie wierzchołków incydentnych zarówno z krawędzią czystą, jak i z krawędzią skażoną. To jednak nie wystarczy. Musimy jeszcze rozważyć sposób przeszukania każdej krawędzi – może się bowiem zdarzyć, że w czasie jej przeszukiwania potrzebnych jest więcej osób niż potrzeba strażników bezpośrednio przed i bezpośrednio po operacji.
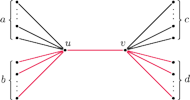
Rys. 2 Moment przeszukiwania krawędzi
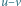 ; kolorowe linie oznaczają krawędzie
skażone.
; kolorowe linie oznaczają krawędzie
skażone.
Rozważmy więc samą operację oczyszczenia pewnej krawędzi
 Załóżmy, że przed jej oczyszczeniem
Załóżmy, że przed jej oczyszczeniem
 jest incydentne z
jest incydentne z
 krawędziami czystymi i
krawędziami czystymi i
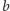 krawędziami skażonymi (nie licząc
krawędziami skażonymi (nie licząc
 ), natomiast
), natomiast
 z
z
 czystymi i z
czystymi i z
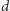 skażonymi
(również nie licząc
skażonymi
(również nie licząc
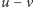 ). Sytuację przedstawia Rys. 2.
). Sytuację przedstawia Rys. 2.
Niech
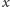 będzie liczbą policjantów potrzebnych do pilnowania
krawędzi tuż przed oczyszczeniem
będzie liczbą policjantów potrzebnych do pilnowania
krawędzi tuż przed oczyszczeniem
 natomiast
natomiast
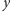 –
tuż po jej oczyszczeniu. Oczyszczenie krawędzi
–
tuż po jej oczyszczeniu. Oczyszczenie krawędzi
 wymaga
wymaga
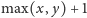 policjantów w sytuacji, gdy spełniony jest następujący
warunek:
policjantów w sytuacji, gdy spełniony jest następujący
warunek:

We wszystkich innych przypadkach potrzeba dokładnie
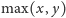 policjantów.
policjantów.
Koszt przeszukania grafu przy zadanej kolejności krawędzi jest równy maksimum z zapotrzebowań na policjantów we wszystkich momentach.
Otrzymujemy więc algorytm o złożoności
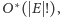 czyli działający
w czasie
czyli działający
w czasie
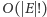 z dokładnością do czynnika wielomianowego (
z dokładnością do czynnika wielomianowego (
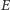 to zbiór krawędzi grafu).
to zbiór krawędzi grafu).
Możemy jednak tę złożoność zmniejszyć do
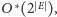 jeżeli
posłużymy się programowaniem dynamicznym – możemy obliczać dla
każdego podzbioru krawędzi minimalną liczbę policjantów potrzebną do
uzyskania danego podzbioru krawędzi czystych. Jeżeli będziemy generowali te
wyniki dla coraz większych podzbiorów krawędzi, to dla każdego z nich
możemy obliczyć wynik w czasie wielomianowym, korzystając z wyników
dla mniejszych zbiorów.
jeżeli
posłużymy się programowaniem dynamicznym – możemy obliczać dla
każdego podzbioru krawędzi minimalną liczbę policjantów potrzebną do
uzyskania danego podzbioru krawędzi czystych. Jeżeli będziemy generowali te
wyniki dla coraz większych podzbiorów krawędzi, to dla każdego z nich
możemy obliczyć wynik w czasie wielomianowym, korzystając z wyników
dla mniejszych zbiorów.
Dokładną specyfikację tego algorytmu pozostawiam jako ćwiczenie dla Czytelnika.
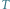 oznacza terrorystę, pozostałe punkty oznaczają policjantów. Kolorowe strzałki pokazują
strategię policjantów.
oznacza terrorystę, pozostałe punkty oznaczają policjantów. Kolorowe strzałki pokazują
strategię policjantów.
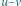 ; kolorowe linie oznaczają krawędzie
skażone.
; kolorowe linie oznaczają krawędzie
skażone.