Odtwarzanie grafu
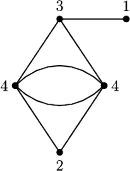
W grafie nieskierowanym możemy obliczyć stopień każdego wierzchołka, czyli liczbę krawędzi incydentnych z tym wierzchołkiem. Przykładowo, dla grafu-koperty otrzymujemy w ten sposób ciąg stopni 4, 4, 3, 3, 2. Wykonanie takiego przekształcenia dla danego grafu jest naprawdę proste. Możemy jednak postawić pytanie odwrotne: czy mając dany ciąg liczb, możemy stwierdzić, czy odpowiada on stopniom wierzchołków jakiegoś grafu nieskierowanego, a jeśli tak, zrekonstruować ten graf?

Rys. 1
Rys. 2
Weźmy, na przykład, ciąg 4, 4, 3, 3, 1 – czy jest on ciągiem stopni jakiegoś grafu? Tutaj łatwo udzielić odpowiedzi negatywnej. Faktycznie, każda krawędź w grafie wpływa na zwiększenie stopni dwóch wierzchołków o jeden, czyli suma stopni musi zawsze być parzysta. A teraz coś bardziej skomplikowanego: ciąg 4, 4, 3, 2, 1. Jeśli dopuszczamy krawędzie wielokrotne, graf możemy odtworzyć, na przykład, tak jak na rysunku 2. To jest jednak multigraf – w „zwykłym” grafie nie możemy mieć krawędzi wielokrotnych ani pętli. Po chwili kombinowania można sprawdzić, że podany ciąg nie odpowiada żadnemu zwykłemu grafowi. Przydałby się jakiś uniwersalny przepis na takie sprawdzanie.
Na szczęście taki przepis – algorytm – istnieje. Jest on przykładem podejścia zachłannego: wybieramy dowolny wierzchołek grafu, czyli element ciągu stopni, po czym łączymy go krawędziami z wierzchołkami o możliwie najwyższych stopniach. Następnie zmniejszamy stopnie tych wierzchołków, usuwamy wybrany wierzchołek z grafu i powtarzamy to samo od początku. Jeśli w pewnym momencie nie uda się znaleźć odpowiedniej liczby wierzchołków o dodatnich stopniach, kończymy algorytm z wynikiem negatywnym. Rozważmy, dla przykładu, początkowy ciąg 4, 4, 3, 3, 2. Wybieramy wierzchołek o stopniu 3 i łączymy go z wierzchołkami o stopniach 4, 4, 3. Nowy ciąg to 3, 3, 2, 2. Wybierzmy ponownie wierzchołek o stopniu 3; łączymy go ze wszystkimi pozostałymi i otrzymujemy ciąg 2, 1, 1. Jeśli teraz ponownie wybierzemy wierzchołek o najwyższym stopniu, to uda nam się skonstruować cały graf, dokładnie taki jak na rysunku 1. Gdybyśmy natomiast zaczęli od ciągu 4, 4, 3, 2, 1 i wybrali kolejno pierwsze dwa wierzchołki (te o początkowym stopniu 4), już w drugim kroku – ciąg 3, 2, 1, 0 – otrzymalibyśmy odpowiedź negatywną.
Wykażemy, że ta metoda, znana też pod nazwą algorytmu Havla–Hakimiego,
zawsze daje poprawne wyniki. W tym celu wystarczy udowodnić, że
jeśli dla danego ciągu liczb istnieje graf, dla którego rozważany ciąg
jest ciągiem stopni wierzchołków, to nasz algorytm taki graf znajdzie.
Załóżmy, przez zaprzeczenie, że nierosnący ciąg
 odpowiada
stopniom wierzchołków pewnego grafu
odpowiada
stopniom wierzchołków pewnego grafu
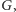 ale nasz algorytm
uruchomiony dla ciągu
ale nasz algorytm
uruchomiony dla ciągu
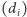 zwrócił odpowiedź negatywną.
Niech
zwrócił odpowiedź negatywną.
Niech
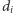 będzie stopniem pierwszego wierzchołka rozważanego
w algorytmie; nazwijmy ten wierzchołek
będzie stopniem pierwszego wierzchołka rozważanego
w algorytmie; nazwijmy ten wierzchołek
 W naszym algorytmie
próbujemy połączyć wierzchołek
W naszym algorytmie
próbujemy połączyć wierzchołek
 z wierzchołkami o stopniach
z wierzchołkami o stopniach
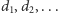 (z pominięciem samego
(z pominięciem samego
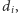 rzecz jasna). Skoro
graf
rzecz jasna). Skoro
graf
 istnieje, to na pewno dla wierzchołka
istnieje, to na pewno dla wierzchołka
 musi nam
się to udać.
musi nam
się to udać.
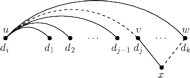
Rys. 3 Podmiana krawędzi
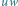 i
i
 na
na
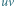 i
i
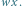
Spytajmy zatem, z jakimi wierzchołkami w
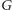 jest połączony
wierzchołek
jest połączony
wierzchołek
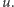 Jeśli z tymi samymi co w naszym algorytmie,
to możemy usunąć wierzchołek
Jeśli z tymi samymi co w naszym algorytmie,
to możemy usunąć wierzchołek
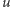 wraz z tymi połączeniami
i rozumować indukcyjnie dla ciągu o jeden wierzchołek krótszego.
Załóżmy więc, że tak nie jest: niech
wraz z tymi połączeniami
i rozumować indukcyjnie dla ciągu o jeden wierzchołek krótszego.
Załóżmy więc, że tak nie jest: niech
 będzie wierzchołkiem
o największym możliwym stopniu
będzie wierzchołkiem
o największym możliwym stopniu
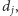 który nie jest połączony z
który nie jest połączony z
 w grafie
w grafie
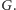 Wierzchołek
Wierzchołek
 musi być zatem połączony w
musi być zatem połączony w
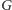 z jakimś innym wierzchołkiem, powiedzmy
z jakimś innym wierzchołkiem, powiedzmy
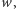 o stopniu
o stopniu
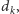 dla
dla
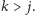 Pokażemy, że możemy w
Pokażemy, że możemy w
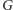 tak
pozamieniać krawędzie, żeby wierzchołek
tak
pozamieniać krawędzie, żeby wierzchołek
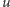 był połączony z
był połączony z
 zamiast z
zamiast z
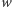 (patrz rysunek 3). Faktycznie, ponieważ
(patrz rysunek 3). Faktycznie, ponieważ
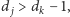 więc w
więc w
 musi istnieć jakiś wierzchołek (nazwijmy
go
musi istnieć jakiś wierzchołek (nazwijmy
go
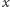 ) połączony z
) połączony z
 i niepołączony z
i niepołączony z
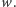 Podmieniając
w grafie
Podmieniając
w grafie
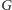 krawędzie
krawędzie
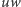 i
i
 na krawędzie
na krawędzie
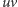 i
i
 otrzymujemy dokładnie to, czego chcieliśmy. Jeśli po wykonaniu
tej operacji zbiór sąsiadów
otrzymujemy dokładnie to, czego chcieliśmy. Jeśli po wykonaniu
tej operacji zbiór sąsiadów
 w
w
 wciąż nie jest tej samej
postaci co w naszym algorytmie, kontynuujemy tego typu podmiany aż
do chwili, kiedy te zbiory sąsiadów będą takie same. Po tym usuwamy
z grafu
wciąż nie jest tej samej
postaci co w naszym algorytmie, kontynuujemy tego typu podmiany aż
do chwili, kiedy te zbiory sąsiadów będą takie same. Po tym usuwamy
z grafu
 wierzchołek
wierzchołek
 wraz z incydentnymi krawędziami
i powtarzamy wcześniejsze rozumowanie na tak zmniejszonym grafie.
Widać, że na końcu otrzymamy dokładnie taki graf, jaki skonstruowałby
nasz algorytm.
wraz z incydentnymi krawędziami
i powtarzamy wcześniejsze rozumowanie na tak zmniejszonym grafie.
Widać, że na końcu otrzymamy dokładnie taki graf, jaki skonstruowałby
nasz algorytm.
Wtręt implementacyjny:
Podany algorytm można zaimplementować
w czasie kwadratowym ze względu na liczbę wierzchołków grafu, czyli
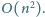 Wystarczy w metodzie zachłannej za każdym razem wybierać
wierzchołek o największym stopniu, czyli odpowiadający elementowi
Wystarczy w metodzie zachłannej za każdym razem wybierać
wierzchołek o największym stopniu, czyli odpowiadający elementowi
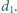 Wówczas obsłużenie tego wierzchołka polega na zmniejszeniu elementów
Wówczas obsłużenie tego wierzchołka polega na zmniejszeniu elementów
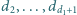 o jeden, usunięciu elementu
o jeden, usunięciu elementu
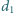 z ciągu i poprawieniu
uporządkowania ciągu. Wszystko to można zrobić w czasie
z ciągu i poprawieniu
uporządkowania ciągu. Wszystko to można zrobić w czasie
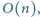 przy czym najmniej oczywistą fazę – przywracanie porządku nierosnącego –
wykonujemy za pomocą co najwyżej jednego odwrócenia fragmentu ciągu,
patrz też rysunek 4.
przy czym najmniej oczywistą fazę – przywracanie porządku nierosnącego –
wykonujemy za pomocą co najwyżej jednego odwrócenia fragmentu ciągu,
patrz też rysunek 4.
Przy nieco ostrożniejszej implementacji można zapisać ten algorytm
w złożoności czasowej proporcjonalnej do sumy elementów ciągu
 czyli w czasie proporcjonalnym do liczby krawędzi konstruowanego
grafu. Jak to zrobić?
czyli w czasie proporcjonalnym do liczby krawędzi konstruowanego
grafu. Jak to zrobić?

Rys. 4 Pierwszy krok algorytmu zachłannego wykonywany dla ciągu 5, 5, 4, 4, 4, 4, 4, 4, 2, 2, 1.
Jeśli jesteśmy zainteresowani tylko binarną informacją – czy podany ciąg jest
ciągiem stopni wierzchołków jakiegoś grafu (czy ciąg jest graficzny) –
możemy posłużyć się jeszcze prostszym kryterium. Pochodzi ono
od Erdősa i Gallaiego (w skrócie EG) i orzeka, że nierosnący ciąg
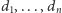 o parzystej sumie jest graficzny wtedy i tylko wtedy, gdy dla
każdego
o parzystej sumie jest graficzny wtedy i tylko wtedy, gdy dla
każdego
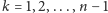 zachodzi nierówność
zachodzi nierówność

Aby zrozumieć sens nierówności EG, pokażemy, że stanowią one
warunek konieczny na graficzność ciągu
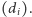 Ustalmy parametr
Ustalmy parametr
 Wówczas po lewej stronie nierówności mamy „zapotrzebowanie na
krawędzie” pierwszych
Wówczas po lewej stronie nierówności mamy „zapotrzebowanie na
krawędzie” pierwszych
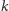 wierzchołków. Owo zapotrzebowanie może
zostać zaspokojone przez krawędzie łączące pewne pary tych wierzchołków –
takich krawędzi może być co najwyżej
wierzchołków. Owo zapotrzebowanie może
zostać zaspokojone przez krawędzie łączące pewne pary tych wierzchołków –
takich krawędzi może być co najwyżej
 a każda z nich ma
wpływ na stopnie dwóch spośród rozważanych wierzchołków – oraz
przez krawędzie łączące pewne z tych wierzchołków z pozostałymi.
Wierzchołek o stopniu
a każda z nich ma
wpływ na stopnie dwóch spośród rozważanych wierzchołków – oraz
przez krawędzie łączące pewne z tych wierzchołków z pozostałymi.
Wierzchołek o stopniu
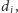
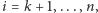 dostarcza co najwyżej
dostarcza co najwyżej
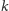 takich krawędzi – po jednej do każdego z wierzchołków
takich krawędzi – po jednej do każdego z wierzchołków
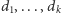 – a zarazem, oczywiście, co najwyżej
– a zarazem, oczywiście, co najwyżej
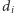 krawędzi,
skąd otrzymujemy konieczność nierówności EG.
krawędzi,
skąd otrzymujemy konieczność nierówności EG.
Z kolei dostateczność warunków EG można próbować pokazać,
wykorzystując własności algorytmu zachłannego. Przykładowo, polecamy
Czytelnikowi pouczające sprawdzenie, że pierwsze dwie nierówności EG są
równoważne temu, iż algorytm zachłanny poprawnie przetworzy kolejno
wierzchołki o stopniach
 i
i
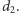 Pełny dowód dostateczności
kryterium EG jest, niestety, bardziej skomplikowany.
Pełny dowód dostateczności
kryterium EG jest, niestety, bardziej skomplikowany.
Wtręt implementacyjny:
Kryterium EG ma także tę przewagę nad algorytmem Havla–Hakimiego, że jego prawdziwość można sprawdzić w czasie liniowym względem liczby wierzchołków grafu. Łatwo zauważyć, że wszystkie sumy prefiksowe i sufiksowe ciągu
 :
:

można obliczyć w czasie
 Wtedy lewa strona
Wtedy lewa strona
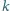 -tej
nierówności EG to dokładnie
-tej
nierówności EG to dokładnie
 Z kolei trochę nietypowe sumy
występujące po prawej stronie nierówności można łatwo obliczyć, jeśli
znamy liczbę elementów ciągu
Z kolei trochę nietypowe sumy
występujące po prawej stronie nierówności można łatwo obliczyć, jeśli
znamy liczbę elementów ciągu
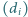 większych niż
większych niż
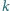 (oznaczenie:
(oznaczenie:
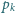 ). Wówczas suma po prawej stronie to
). Wówczas suma po prawej stronie to
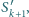 jeśli
jeśli
 natomiast w przeciwnym przypadku jest ona równa
natomiast w przeciwnym przypadku jest ona równa
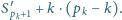 Wreszcie ciąg
Wreszcie ciąg
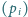 możemy wyznaczyć
w czasie
możemy wyznaczyć
w czasie
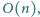 i to na kilka różnych sposobów.
i to na kilka różnych sposobów.
Warto na koniec wspomnieć o jeszcze jednym kryterium graficzności ciągu.
Nie jest ono efektywniejsze ani bardziej praktyczne od kryterium EG, ale za to
wygląda bardziej egzotycznie. Załóżmy, że
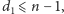 w przeciwnym
przypadku mamy natychmiast odpowiedź negatywną. Rozważmy macierz
zero-jedynkową
w przeciwnym
przypadku mamy natychmiast odpowiedź negatywną. Rozważmy macierz
zero-jedynkową
 wymiaru
wymiaru
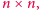 o zerowej przekątnej, w której
o zerowej przekątnej, w której
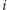 -ty wiersz zawiera
-ty wiersz zawiera
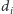 jedynek dopchniętych do lewej strony –
z uwzględnieniem jednak zerowej przekątnej. Niech
jedynek dopchniętych do lewej strony –
z uwzględnieniem jednak zerowej przekątnej. Niech
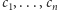 będzie
ciągiem sum w kolumnach macierzy
będzie
ciągiem sum w kolumnach macierzy
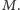 Wówczas kryterium
Gale’a–Rysera orzeka, że ciąg
Wówczas kryterium
Gale’a–Rysera orzeka, że ciąg
 jest graficzny wtedy i tylko wtedy, gdy
sumy prefiksowe ciągu
jest graficzny wtedy i tylko wtedy, gdy
sumy prefiksowe ciągu
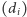 są zdominowane przez sumy prefiksowe ciągu
są zdominowane przez sumy prefiksowe ciągu
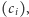 tzn.
tzn.

Wnikliwemu Czytelnikowi pozostawiamy podanie związku między tym kryterium a warunkami EG.
Na koniec kilka pytań do Czytelnika. Jakie warunki musi spełniać ciąg stopni
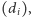 żeby dało się z niego odtworzyć graf, który jest spójny? A jakie,
żeby odpowiadał stopniom wierzchołków jakiegoś grafu dwudzielnego? No
dobrze, to drugie zadanie jest dosyć trudne. Ale jakie warunki musi spełniać
para ciągów
żeby dało się z niego odtworzyć graf, który jest spójny? A jakie,
żeby odpowiadał stopniom wierzchołków jakiegoś grafu dwudzielnego? No
dobrze, to drugie zadanie jest dosyć trudne. Ale jakie warunki musi spełniać
para ciągów
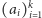 i
i
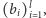 tak aby istniał graf dwudzielny,
w którym
tak aby istniał graf dwudzielny,
w którym
 odpowiada stopniom wierzchołków z jednej grupy, a
odpowiada stopniom wierzchołków z jednej grupy, a
 – wierzchołkom z drugiej grupy?
– wierzchołkom z drugiej grupy?
 i
i
 na
na
 i
i
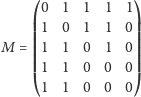
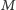 skonstruowana dla ciągu graficznego 4, 3, 3, 2, 2. Ciąg sum
w kolumnach tej macierzy to 4, 4, 2, 3, 1.
skonstruowana dla ciągu graficznego 4, 3, 3, 2, 2. Ciąg sum
w kolumnach tej macierzy to 4, 4, 2, 3, 1.