Informatyczny kącik olimpijski
Myjnia samochodowa
Zadanie omawiane w tym kąciku pochodzi z obozu treningowego drużyn rosyjskich z 2008 roku (autor zadania: Andrew Stankevich).
Zadanie. Do myjni ustawiła się długa kolejka samochodów (jest ich
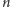 ), z których każdy należy wyczyścić w środku i umyć
od zewnątrz. Dla samochodu o numerze
), z których każdy należy wyczyścić w środku i umyć
od zewnątrz. Dla samochodu o numerze
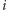 czynności te zajmują,
odpowiednio,
czynności te zajmują,
odpowiednio,
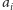 oraz
oraz
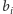 sekund i są wykonywane niezależnie
przez dwie różne osoby – jeden pracownik myje wszystkie samochody od
zewnątrz, a drugi czyści wszystkie od wewnątrz. Każdy z pracowników
może dowolnie ustalić kolejność czyszczenia samochodów. Każdy
pracownik może pracować naraz tylko nad jednym samochodem i każdy
samochód może być w jednej chwili czyszczony przez tylko jednego
pracownika. Zadaniem jest takie ustalenie kolejności czyszczenia przez obu
pracowników, żeby jak najszybciej zakończyć całą pracę.
sekund i są wykonywane niezależnie
przez dwie różne osoby – jeden pracownik myje wszystkie samochody od
zewnątrz, a drugi czyści wszystkie od wewnątrz. Każdy z pracowników
może dowolnie ustalić kolejność czyszczenia samochodów. Każdy
pracownik może pracować naraz tylko nad jednym samochodem i każdy
samochód może być w jednej chwili czyszczony przez tylko jednego
pracownika. Zadaniem jest takie ustalenie kolejności czyszczenia przez obu
pracowników, żeby jak najszybciej zakończyć całą pracę.
W prawdziwej myjni prawdopodobnie liczby
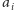 nie różnią się zbytnio,
podobnie jest w przypadku liczb
nie różnią się zbytnio,
podobnie jest w przypadku liczb
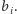 Zachęcamy Czytelnika do zastanowienia
się, czy dodatkowe założenie, że
Zachęcamy Czytelnika do zastanowienia
się, czy dodatkowe założenie, że
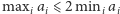 i analogicznie dla
i analogicznie dla
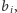 pomaga w znalezieniu rozwiązania. W oryginalnym zadaniu
jednak takich założeń nie było, zastanówmy się więc, jak je rozwiązać
bez tego.
pomaga w znalezieniu rozwiązania. W oryginalnym zadaniu
jednak takich założeń nie było, zastanówmy się więc, jak je rozwiązać
bez tego.
Oznaczmy przez
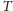 najkrótszy czas, w którym można zakończyć pracę. Łatwo
zauważyć, że
najkrótszy czas, w którym można zakończyć pracę. Łatwo
zauważyć, że
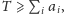
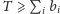 oraz
oraz
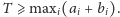 Niech
Niech
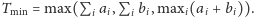 Chcielibyśmy ułożyć plan,
w którym
Chcielibyśmy ułożyć plan,
w którym
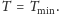 Jeśli
Jeśli
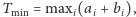 rozważmy
rozważmy
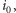 które realizuje to maksimum. Wiemy wówczas, iż
które realizuje to maksimum. Wiemy wówczas, iż
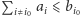 oraz
oraz
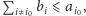 czyli możemy ustalić, że jeden
z pracowników najpierw czyści wszystkie samochody poza
czyli możemy ustalić, że jeden
z pracowników najpierw czyści wszystkie samochody poza
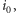 a drugi
w tym czasie czyści samochód
a drugi
w tym czasie czyści samochód
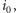 po czym zamieniają się. W ten
sposób otrzymujemy plan spełniający
po czym zamieniają się. W ten
sposób otrzymujemy plan spełniający
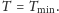 Pozostał nam przypadek,
w którym
Pozostał nam przypadek,
w którym
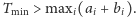 Możemy w nim bez straty ogólności
założyć, że
Możemy w nim bez straty ogólności
założyć, że
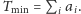 W takiej sytuacji przeprowadzimy
rozumowanie indukcyjne. Jeśli są co najwyżej dwa samochody, sprawa jest
oczywista. Jeśli są dokładnie trzy, to nie mogą zachodzić jednocześnie
nierówności
W takiej sytuacji przeprowadzimy
rozumowanie indukcyjne. Jeśli są co najwyżej dwa samochody, sprawa jest
oczywista. Jeśli są dokładnie trzy, to nie mogą zachodzić jednocześnie
nierówności
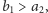
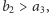
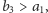 bo mielibyśmy,
wbrew założeniom,
bo mielibyśmy,
wbrew założeniom,
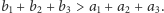 Bez straty ogólności
załóżmy, że
Bez straty ogólności
załóżmy, że
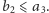 Jeśli dodatkowo
Jeśli dodatkowo
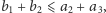 to
widzimy, że można ustawić samochody następująco: u pierwszego
pracownika
to
widzimy, że można ustawić samochody następująco: u pierwszego
pracownika
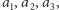 a u drugiego
a u drugiego
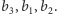 Jeśli zaś nie, to
naturalnie
Jeśli zaś nie, to
naturalnie
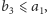 a stąd
a stąd
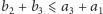 i sytuacja jest zupełnie
analogiczna.
i sytuacja jest zupełnie
analogiczna.
Załóżmy w takim razie, że umiemy rozplanować czyszczenie dowolnych
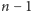 samochodów, i zastanówmy się, jak wyczyścić dane
samochodów, i zastanówmy się, jak wyczyścić dane
 samochodów (
samochodów (
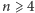 ). Niech dwoma samochodami o najmniejszej
sumie
). Niech dwoma samochodami o najmniejszej
sumie
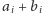 będą te o numerach
będą te o numerach
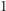 i
i
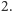 Ustalmy, że
samochód drugi będzie czyszczony przez każdego z pracowników tuż po
pierwszym, oraz załóżmy dodatkowo, że w czasie, gdy jeden z pracowników
czyści którykolwiek z tych samochodów, drugi pracownik nie może
czyścić drugiego z tych samochodów. Innymi słowy, zamieniamy
te dwa samochody w jeden, o współczynnikach
Ustalmy, że
samochód drugi będzie czyszczony przez każdego z pracowników tuż po
pierwszym, oraz załóżmy dodatkowo, że w czasie, gdy jeden z pracowników
czyści którykolwiek z tych samochodów, drugi pracownik nie może
czyścić drugiego z tych samochodów. Innymi słowy, zamieniamy
te dwa samochody w jeden, o współczynnikach
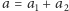 i
i
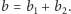 Dla nowego zestawu samochodów mamy:
Dla nowego zestawu samochodów mamy:

Zauważmy, że z wyboru samochodów
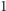 i
i
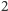 wynika, że
wynika, że
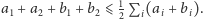 Stąd
Stąd
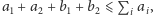 czyli
ostatecznie
czyli
ostatecznie
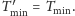 Z założenia indukcyjnego
Z założenia indukcyjnego
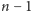 otrzymanych
po zamianie samochodów można wyczyścić w czasie
otrzymanych
po zamianie samochodów można wyczyścić w czasie
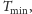 a więc
tym bardziej wyjściowe
a więc
tym bardziej wyjściowe
 samochodów można wyczyścić w czasie
samochodów można wyczyścić w czasie
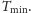 To pokazuje, że
To pokazuje, że
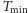 jest szukanym minimalnym czasem
czyszczenia samochodów w dowolnym przypadku.
jest szukanym minimalnym czasem
czyszczenia samochodów w dowolnym przypadku.
Zauważmy, że nasz dowód jest w pełni konstruktywny: tak długo, jak
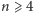 i
i
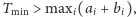 wybieramy dwa samochody
o najmniejszej sumie
wybieramy dwa samochody
o najmniejszej sumie
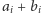 i łączymy je w jeden. Przy użyciu
odpowiedniej struktury danych (chociażby kopca) tę procedurę można
zrealizować w czasie
i łączymy je w jeden. Przy użyciu
odpowiedniej struktury danych (chociażby kopca) tę procedurę można
zrealizować w czasie
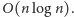 Następnie rozwiązujemy problem dla
trzech samochodów lub dla przypadku
Następnie rozwiązujemy problem dla
trzech samochodów lub dla przypadku
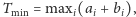 co możemy
wykonać w czasie stałym lub, odpowiednio,
co możemy
wykonać w czasie stałym lub, odpowiednio,
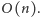 Na końcu
odzyskujemy rozwiązanie całości poprzez podstawianie, kolejno, par
samochodów w miejsce tych sztucznie stworzonych.
Na końcu
odzyskujemy rozwiązanie całości poprzez podstawianie, kolejno, par
samochodów w miejsce tych sztucznie stworzonych.