Krowa, las i eksploracja terenu
Kilkanaście lat temu zgubiłem się w lesie. Nie na tyle, żeby sytuacja była beznadziejna...
Rys. 1
Rys. 2
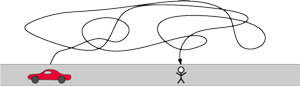
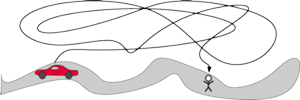
Wiedziałem, że zostawiłem auto przy drodze, wszedłem do lasu, gdzie spędziłem jakiś czas, chodząc, a następnie wróciłem do tej samej drogi. Dodatkowo, podczas spaceru po lesie przeciąłem swoją drogę dostatecznie dużo razy, żeby nie mieć zielonego pojęcia, czy samochodu należy szukać, idąc w lewą stronę czy w prawą. Ot, mniej więcej tak jak na rysunku 1.
To znaczy, drzewa na tyle skutecznie zasłaniały drogę, że widoczność była praktycznie zerowa. Nie miałem szans zobaczyć samochodu z odległości, musiałem się na niego natknąć.
Parę lat później (pomińmy chwilowo milczeniem to, ile się nachodziłem w drodze do samochodu) dowiedziałem się, że ktoś już wcześniej miał taki sam problem i zostało to dokładnie opisane w literaturze. A mianowicie, ten sam problem miała pewna krowa.
Krowa jaka jest, każdy widzi
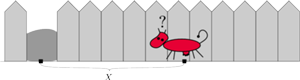
Rys. 3
Krowa stoi przy prostym płocie, w którym jest wejście na pastwisko. Wejście (które jest oddalone od krowy o co najmniej jeden metr) krowa zobaczy dopiero, gdy do niego dotrze. Co powinna zrobić, żeby jak najszybciej rozpocząć zjadanie trawy? Problem ten jest jednym z najprostszych wariantów zagadnienia eksploracji terenu. Jak okaże się poniżej, prostym, lecz nie trywialnym.
Postarajmy się wyrobić sobie podstawowe intuicje. W całym artykule
przez
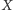 będziemy oznaczać początkową odległość, w metrach,
dzielącą krowę od wejścia na pastwisko. Oczywiście, absolutnie genialna
krowa, znająca mapę terenu, potrafi dojść na pastwisko, przeszedłszy
będziemy oznaczać początkową odległość, w metrach,
dzielącą krowę od wejścia na pastwisko. Oczywiście, absolutnie genialna
krowa, znająca mapę terenu, potrafi dojść na pastwisko, przeszedłszy
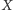 metrów. Co się dzieje, jeśli krowa jest trochę głupsza, czyli nie zna
mapy, nie zna
metrów. Co się dzieje, jeśli krowa jest trochę głupsza, czyli nie zna
mapy, nie zna
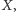 ale wie, że wejście na pastwisko jest z prawej strony?
Oczywiście, idąc uparcie w tym kierunku, przejdzie też dokładnie
ale wie, że wejście na pastwisko jest z prawej strony?
Oczywiście, idąc uparcie w tym kierunku, przejdzie też dokładnie
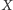 metrów.
metrów.
A co ma zrobić krowa, jeśli w jakiś sposób poznała wartość
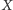 (przykładowo, wie, że od wymarzonego celu dzieli ją 10 metrów), ale
nie wie, czy wejście jest z lewej, czy z prawej? Może wtedy zastosować
następujący algorytm z parametrem
(przykładowo, wie, że od wymarzonego celu dzieli ją 10 metrów), ale
nie wie, czy wejście jest z lewej, czy z prawej? Może wtedy zastosować
następujący algorytm z parametrem
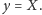
Algorytm Go-and-Eat(y)
- 1.
- Idź
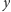 metrów w lewo
metrów w lewo
- 2.
- Jeśli nie znajdziesz wejścia, zawróć do punktu startowego
- 3.
- Idź
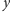 metrów w prawo
metrów w prawo
Łatwo obliczyć, że w najgorszym przypadku (a tylko takie przypadki interesują
biedne, pechowe krowy) krowa przejdzie
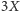 metrów (czyli w naszym
przykładzie trzydzieści). Uważny Czytelnik zauważy, że to, czy krowa idzie
na początku w lewo czy w prawo, w pewnym sensie nie ma znaczenia: jeśli
krowa ma pecha, to wejście będzie i tak z drugiej strony niż ta, którą
wybierze.
metrów (czyli w naszym
przykładzie trzydzieści). Uważny Czytelnik zauważy, że to, czy krowa idzie
na początku w lewo czy w prawo, w pewnym sensie nie ma znaczenia: jeśli
krowa ma pecha, to wejście będzie i tak z drugiej strony niż ta, którą
wybierze.
Krowa głodna to krowa zła
Prawdziwy problem krowy (który jest identyczny z moim poszukiwaniem
samochodu) zaczyna się jednak wtedy, kiedy krowa nie zna ani wartości
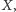 ani nie wie, z której strony jest wejście. Zamiast wyciągnąć gotowe
rozwiązanie z kapelusza, zastanówmy się, co mogłoby pomóc krowie w tym
zadaniu.
ani nie wie, z której strony jest wejście. Zamiast wyciągnąć gotowe
rozwiązanie z kapelusza, zastanówmy się, co mogłoby pomóc krowie w tym
zadaniu.
A gdyby krowa znała jakieś oszacowanie na
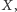 na przykład znała pewną
liczbę
na przykład znała pewną
liczbę
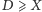 ? Mogłaby uruchomić procedurę Go-and-Eat(D) tj. iść
? Mogłaby uruchomić procedurę Go-and-Eat(D) tj. iść
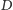 metrów w lewo, wrócić do punktu wyjścia, a następnie
iść w prawo. Przebyta droga w najgorszym przypadku wynosiłaby
metrów w lewo, wrócić do punktu wyjścia, a następnie
iść w prawo. Przebyta droga w najgorszym przypadku wynosiłaby
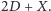 Czyli jeśli
Czyli jeśli
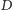 byłoby „tylko trochę” większe od
byłoby „tylko trochę” większe od
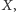 to otrzymalibyśmy rozwiązanie niedużo gorsze niż w przypadku,
kiedy znamy
to otrzymalibyśmy rozwiązanie niedużo gorsze niż w przypadku,
kiedy znamy
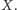 No dobrze, ale jak znaleźć takie
No dobrze, ale jak znaleźć takie
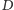 ? Pomoże
nam w tym często stosowana w algorytmice metoda podwajania: uruchamiamy
algorytm Go-and-Eat kolejno z wartościami
? Pomoże
nam w tym często stosowana w algorytmice metoda podwajania: uruchamiamy
algorytm Go-and-Eat kolejno z wartościami
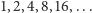 Cieszą nas
dwie własności.
Cieszą nas
dwie własności.
- Jeśli w końcu uruchomimy Go-and-Eat z potęgą liczby 2
większą od
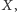 to krowa znajdzie pastwisko.
to krowa znajdzie pastwisko.
- Sumaryczna droga przebyta podczas uruchamiania Go-and-Eat ze zbyt małymi wartościami parametru jest niezbyt długa. (To dopiero wykażemy.)
Ale moment! – powinien krzyknąć Uważny Czytelnik. Przecież po uruchomieniu algorytmu Go-and-Eat(1) krowa znajdzie się o 1 metr od punktu wyjścia, a algorytm Go-and-Eat(2) ma szansę zadziałać pod warunkiem, że krowa znajduje się początkowo w punkcie startowym. Możemy „załatać” algorytm, dodając do niego dodatkowy krok:
- 4.
- Zawróć do punktu startowego
Łata na łacie
Tu mała dygresja – informatycy, jak i wszystkie umysły ścisłe, uwielbiają: a) łatanie złych rozwiązań zamiast pisania ich od nowa, b) redukcje. Do tego stopnia uwielbiają, że często wpadają w pułapki jak w opisanej niżej historii (z długaśną brodą) o czajniku:
Mamy pusty czajnik, chcemy zagotować wodę. Co zrobić? Należy oczywiście: 1. nalać wody, 2. włączyć czajnik, 3. czekać. A co zrobić, jeśli mamy pełny czajnik i chcemy zagotować wodę? To proste – odpowie prawdziwy (i leniwy) informatyk – wylewamy z niego wodę i w ten sposób doprowadzamy sytuację do przypadku, który potrafimy rozwiązać.
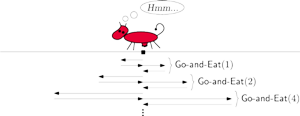
Rys. 4
Zastanówmy się zatem, czy przez „łatanie” algorytmu Go-and-Eat i dodanie punktu 4. nie postąpiliśmy przypadkiem jak prawdziwi informatycy (a nie chcielibyśmy tego robić, bo po co męczyć steraną życiem i mocno już wygłodniałą krowę). Zobaczmy, jak wygląda droga, po której teraz chodzi krowa.
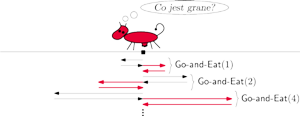
Rys. 5
Może nie jest oczywiste, co można tutaj poprawić. Ale
 pamiętacie,
że to, w którą stronę krowa zaczyna wykonywanie algorytmu Go-and-Eat,
nie ma znaczenia? W takim razie narysujmy drogę krowy, która nieparzyste
wykonania algorytmu Go-and-Eat zaczyna w stronę lewą, a parzyste
w prawą.
pamiętacie,
że to, w którą stronę krowa zaczyna wykonywanie algorytmu Go-and-Eat,
nie ma znaczenia? W takim razie narysujmy drogę krowy, która nieparzyste
wykonania algorytmu Go-and-Eat zaczyna w stronę lewą, a parzyste
w prawą.
Bez sensu, prawda? Krowa idzie w jedną stronę
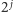 metrów tylko
po to, żeby wrócić do punktu wyjścia i pójść w tę samą stronę
metrów tylko
po to, żeby wrócić do punktu wyjścia i pójść w tę samą stronę
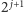 metrów! Wyrzućmy zatem nadmiarowe spacery (zaznaczone
kolorem na poprzednim rysunku). Zmodyfikowany algorytm prezentuje się
następująco:
metrów! Wyrzućmy zatem nadmiarowe spacery (zaznaczone
kolorem na poprzednim rysunku). Zmodyfikowany algorytm prezentuje się
następująco:
Algorytm Smart-Cow
- 1.
- Kierunek zwiedzania := lewo
- 2.
-
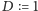
- 3.
- Dopóki nie znalazłeś wejścia na pastwisko, powtarzaj:
- a)
- Przejdź
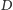 metrów w kierunku zwiedzania i wróć do
punktu startowego
metrów w kierunku zwiedzania i wróć do
punktu startowego
- b)
-
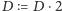
- c)
- Odwróć kierunek zwiedzania
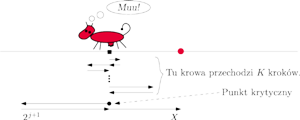
Rys. 6
Spróbujmy teraz przeanalizować, jaki dystans pokona krowa
w najgorszym przypadku. Weźmy takie naturalne
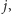 że zachodzi
że zachodzi
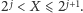 Oznacza to, że pierwsze
Oznacza to, że pierwsze
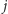 wykonań pętli
w punkcie 3. powyższego algorytmu (z wartościami
wykonań pętli
w punkcie 3. powyższego algorytmu (z wartościami
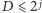 )
nie spowoduje znalezienia pastwiska. Droga przebyta przez krowę do tego
punktu wynosi
)
nie spowoduje znalezienia pastwiska. Droga przebyta przez krowę do tego
punktu wynosi

Nazwijmy ten punkt krytycznym, przyda się on w dalszej części artykułu.
Następnie krowa chce iść
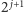 metrów w jakimś kierunku.
Oczywiście, ma pecha i idzie w kierunku przeciwnym do wejścia na
pastwisko. Ten skok w niewłaściwy bok (wraz z powrotem) kosztuje ją
kolejne
metrów w jakimś kierunku.
Oczywiście, ma pecha i idzie w kierunku przeciwnym do wejścia na
pastwisko. Ten skok w niewłaściwy bok (wraz z powrotem) kosztuje ją
kolejne
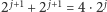 metrów. Następnie krowa zamierza iść
metrów. Następnie krowa zamierza iść
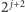 metrów, ale już po
metrów, ale już po
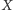 metrach napotyka pastwisko. Jej
całkowita droga to co najwyżej
metrach napotyka pastwisko. Jej
całkowita droga to co najwyżej

Czy naprawdę trzeba tyle chodzić?
Krótka odpowiedź brzmi: tak, każdy algorytm dla krowy wymaga w najgorszym
przypadku przejścia odległości dziewięciokrotnie przekraczającej początkową
odległość krowy od pastwiska. Niestety, wykazanie tego jest dość trudne
i wykracza poza ramy tego artykułu. Spróbujmy jednak uspokoić swoje
sumienie i sprawdzić, że krowa zawsze musi przejść co najmniej
dystans
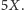 W tym celu zauważmy, że jeśli krowa nie robi
głupich wycieczek (takich jak na dwóch wcześniejszych rysunkach),
to wędruje, oddalając się od punktu startowego na przemian w lewo
i w prawo.
W tym celu zauważmy, że jeśli krowa nie robi
głupich wycieczek (takich jak na dwóch wcześniejszych rysunkach),
to wędruje, oddalając się od punktu startowego na przemian w lewo
i w prawo.
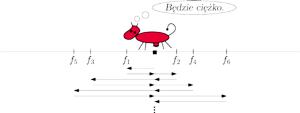
Rys. 7
Wyznacza to podział trasy krowy na kolejne fazy. Bez straty ogólności
załóżmy, że na początku krowa idzie w lewo. Wtedy jej trasę można
opisać liczbami
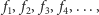 gdzie
gdzie
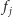 jest oddaleniem
w fazie
jest oddaleniem
w fazie
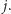 (W opisanym wcześniej algorytmie Smart-Cow mamy
(W opisanym wcześniej algorytmie Smart-Cow mamy
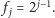 )
)
Zauważmy teraz, że krowa wybiera taką samą trasę niezależnie od tego, jakie
jest
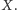 Powyższe zdanie wydaje się oczywiste (jak trasa mogłaby od tego
zależeć, skoro
Powyższe zdanie wydaje się oczywiste (jak trasa mogłaby od tego
zależeć, skoro
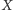 poznajemy dopiero w momencie odnalezienia
pastwiska, a wtedy już nigdzie nie chodzimy?), ale warto je przeczytać
więcej niż raz. Oznacza to, że dla danego wyboru trasy krowy (tj. liczb
poznajemy dopiero w momencie odnalezienia
pastwiska, a wtedy już nigdzie nie chodzimy?), ale warto je przeczytać
więcej niż raz. Oznacza to, że dla danego wyboru trasy krowy (tj. liczb
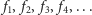 ) wystarczy postawić bramkę na pastwisko w jakimś
bardzo złośliwym miejscu.
) wystarczy postawić bramkę na pastwisko w jakimś
bardzo złośliwym miejscu.
Przypatrzmy się bliżej ciągowi
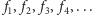 Musi w nim istnieć jakaś
taka kolejna para
Musi w nim istnieć jakaś
taka kolejna para
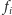 i
i
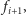 że
że
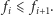 Na powyższym
rysunku jest to, na przykład, para
Na powyższym
rysunku jest to, na przykład, para
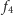 i
i
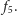 W przeciwnym
przypadku ciąg
W przeciwnym
przypadku ciąg
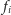 byłby ściśle malejący (a jest to dość kiepski
pomysł, jeśli krowa zamierza znaleźć odległe pastwisko). Załóżmy,
że odległość
byłby ściśle malejący (a jest to dość kiepski
pomysł, jeśli krowa zamierza znaleźć odległe pastwisko). Załóżmy,
że odległość
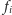 krowa przechodzi w prawą stronę. Postawmy zatem
bramkę kawałeczek dalej niż w odległości
krowa przechodzi w prawą stronę. Postawmy zatem
bramkę kawałeczek dalej niż w odległości
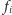 po prawej stronie od
punktu startowego, tj.
po prawej stronie od
punktu startowego, tj.
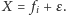
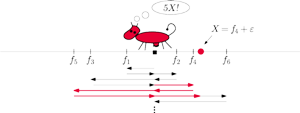
Rys. 8
Wtedy krowa przechodzi co najmniej
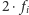 w prawo, potem
w prawo, potem
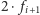 w lewo, a następnie (pod warunkiem, że nie jest bezdennie
głupia i
w lewo, a następnie (pod warunkiem, że nie jest bezdennie
głupia i
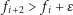 ) krowa dochodzi do pastwiska, przeszedłszy
odległość
) krowa dochodzi do pastwiska, przeszedłszy
odległość
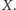 Całkowita droga przebyta przez krowę to
Całkowita droga przebyta przez krowę to

Ponieważ
 możemy wybrać dowolnie małe i zaniedbywalne, krowa
przechodzi praktycznie pięciokrotnie więcej niż
możemy wybrać dowolnie małe i zaniedbywalne, krowa
przechodzi praktycznie pięciokrotnie więcej niż
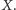
Po co krowie pieniądze?
Jak można ułatwić życie naszej krowie? Na początku poprzedniego rozdziału powiedzieliśmy, że nie da się poprawić wyniku osiąganego przez algorytm Smart-Cow. Cóż, jest to tylko częściowa prawda. Nie można go poprawić, jeśli krowa chodzi deterministycznie. Możemy natomiast podarować jej monetę, którą może wspomóc się w trudnych chwilach (i nie chodzi nam o to, żeby kupiła sobie za to mapę czy coś do jedzenia)
Wróćmy do algorytmu Smart-Cow. Załóżmy, że w momencie, który
nazwaliśmy krytycznym, krowa rzuca monetą. Jeśli wypadnie orzeł, idzie
następne
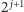 metrów w prawo, w przeciwnym przypadku w lewo. Dla
ustalonej pozycji bramki na pastwisko krowa ma
metrów w prawo, w przeciwnym przypadku w lewo. Dla
ustalonej pozycji bramki na pastwisko krowa ma
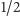 szansy na to, że
pójdzie w jej stronę. W takim przypadku części spaceru krowy (kolorowy
fragment rysunku) o długości
szansy na to, że
pójdzie w jej stronę. W takim przypadku części spaceru krowy (kolorowy
fragment rysunku) o długości
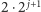 w ogóle nie ma! Wtedy krowa
przechodzi nie
w ogóle nie ma! Wtedy krowa
przechodzi nie
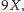 a
a
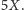 W średnim przypadku przechodzi
zatem
W średnim przypadku przechodzi
zatem
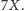
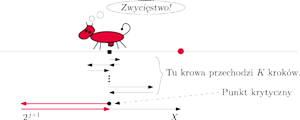
Rys. 9
To obniża średnią liczbę metrów przebytą przez krowę, pod warunkiem że
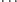 krowa wymyśli, iż dany moment jest krytyczny! Okazuje się jednak,
że wcale nie musi tego robić. Wystarczy, żeby rzuciła monetą, wybierając
kierunek na samym początku. Wtedy analiza jest dokładnie taka sama,
a dodatkowo, w momencie kiedy krowa znajdzie się już w punkcie
krytycznym, z prawdopodobieństwem
krowa wymyśli, iż dany moment jest krytyczny! Okazuje się jednak,
że wcale nie musi tego robić. Wystarczy, żeby rzuciła monetą, wybierając
kierunek na samym początku. Wtedy analiza jest dokładnie taka sama,
a dodatkowo, w momencie kiedy krowa znajdzie się już w punkcie
krytycznym, z prawdopodobieństwem
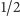 będzie szła w lewo,
a z prawdopodobieństwem
będzie szła w lewo,
a z prawdopodobieństwem
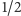 – w prawo.
– w prawo.
Quo vadis, droga krowo?
Powyższe rozważania to tylko czubek góry lodowej tematyki eksploracji terenu. Oprócz „prawdziwych” zastosowań, istnieje jeszcze parę lepiej lub gorzej zbadanych podstawowych problemów. Przykładowo, Czytelnik Dociekliwy może zastanowić się, jaką strategię należy obrać, jeśli jest się kapitanem, który odpłynął od brzegu i stracił orientację. Zakładamy, że linia brzegowa jest linią prostą i chcemy dopłynąć do jej dowolnego miejsca. Możemy wyobrazić sobie następujące warianty tego problemu:
- Wiadomo, że linia brzegowa jest oddalona o 1 km, ale nie wiadomo, w którym kierunku.
- Mamy kompas i wiemy, że linia brzegowa przebiega albo z północy na południe, albo z zachodu na wschód, nie znamy natomiast odległości od linii brzegowej. (Warto zauważyć, że jeśli wiedzielibyśmy np., że linia brzegowa przebiega z północy na południe, to jest to taki sam problem, jaki miała nasza krowa.)
- Nic nie wiemy.
Temperować ołówki, siodłać krowy i do dzieła!