Kolejność ma znaczenie
Z artykułu Wojciecha Śmietanki wypływa ważny morał: przystosowanie algorytmu do działania na maszynie równoległej wymaga często zupełnie innego spojrzenia na dany problem. Okazuje się jednak, że nawet w przypadku architektury jednoprocesorowej optymalizacja algorytmu może wymagać od nas całkiem pomysłowych przeróbek. W tym artykule podamy dwa przykłady, w których kluczową okaże się kolejność, w jakiej wykonujemy operacje.
Za pierwszy przykład niech posłuży wspomniany już algorytm mnożenia macierzy. Można go zapisać, na przykład, tak:

Z uwagi na przemienność dodawania nie ma znaczenia, w jakiej kolejności
wykonamy powyższe pętle. Ważne jest tylko to, aby ostatni wiersz został
wykonany dla wszystkich trójek
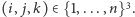 Okazuje się, że to,
iż pętle występują w kolejności
Okazuje się, że to,
iż pętle występują w kolejności
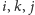 (zamiast, wydawać by się
mogło, bardziej naturalnej kolejności
(zamiast, wydawać by się
mogło, bardziej naturalnej kolejności
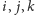 ), ma kluczowe znaczenie.
Na moim komputerze ten program dla
), ma kluczowe znaczenie.
Na moim komputerze ten program dla
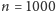 wykonuje się 2,1 s,
natomiast program „naturalny” aż 8,2 s – prawie cztery razy wolniej!
Wiąże się to z tym, że w powyższym programie wszystkie macierze są
przeglądane wierszami, co dobrze wpływa na wykorzystanie pamięci podręcznej
procesora.
wykonuje się 2,1 s,
natomiast program „naturalny” aż 8,2 s – prawie cztery razy wolniej!
Wiąże się to z tym, że w powyższym programie wszystkie macierze są
przeglądane wierszami, co dobrze wpływa na wykorzystanie pamięci podręcznej
procesora.
Często, aby umożliwić wykonywanie operacji w lepszej kolejności, konieczne jest głębsze przebudowanie algorytmu. Za przykład posłuży nam tu wyznaczanie liczb pierwszych za pomocą sita Eratostenesa.

Zauważmy, że dla każdej nowo znalezionej liczby pierwszej
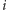 przeglądamy prawie całą tablicę
przeglądamy prawie całą tablicę
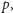 by wykreślić wielokrotności
by wykreślić wielokrotności
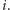 To powoduje, że nieefektywnie korzystamy z pamięci podręcznej
procesora. Spróbujmy zatem tak przepisać powyższy algorytm, by zwiększyć
lokalność odwołań do pamięci.
To powoduje, że nieefektywnie korzystamy z pamięci podręcznej
procesora. Spróbujmy zatem tak przepisać powyższy algorytm, by zwiększyć
lokalność odwołań do pamięci.
Zauważmy, że liczba pierwsza
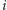 zostanie użyta do wykreślania tylko, gdy
zostanie użyta do wykreślania tylko, gdy
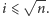 Na początek wykonajmy więc powyższy kod dla początkowego
kawałka tablicy
Na początek wykonajmy więc powyższy kod dla początkowego
kawałka tablicy
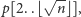 przy okazji zapamiętując w tablicy
przy okazji zapamiętując w tablicy
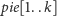 napotkane liczby pierwsze, a w tablicy
napotkane liczby pierwsze, a w tablicy
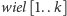 ich
najmniejsze wielokrotności większe niż
ich
najmniejsze wielokrotności większe niż
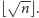 Resztę tablicy
podzielmy na bloki długości
Resztę tablicy
podzielmy na bloki długości
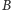 i przeglądajmy te bloki kolejno,
za każdym razem wykreślając (dla wszystkich
i przeglądajmy te bloki kolejno,
za każdym razem wykreślając (dla wszystkich
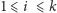 ) znajdujące się
w tym bloku wielokrotności liczby
) znajdujące się
w tym bloku wielokrotności liczby
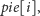 odpowiednio uaktualniając w
odpowiednio uaktualniając w
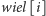 najmniejszą niewykorzystaną jeszcze wielokrotność
najmniejszą niewykorzystaną jeszcze wielokrotność
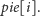 Poniższy pseudokod realizuje ten nowy algorytm:
Poniższy pseudokod realizuje ten nowy algorytm:

Jeśli przyjmiemy
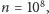 to pierwszy kod działa na moim
komputerze 4,2 s. Pamięć podręczna w moim procesorze ma rozmiar 32 kB,
zatem możemy przyjąć
to pierwszy kod działa na moim
komputerze 4,2 s. Pamięć podręczna w moim procesorze ma rozmiar 32 kB,
zatem możemy przyjąć
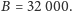 Wtedy drugi program działa
w czasie 1,3 s, co daje ponadtrzykrotne przyspieszenie, mimo iż liczba operacji
wykonywanych w pseudokodzie wzrosła!
Wtedy drugi program działa
w czasie 1,3 s, co daje ponadtrzykrotne przyspieszenie, mimo iż liczba operacji
wykonywanych w pseudokodzie wzrosła!
Można, oczywiście, dalej optymalizować nasz algorytm, np. wyrzucić
z tablicy
 liczby parzyste i użyć tablicy bitowej. Można również
przyjąć jako rozmiar bloku wielokrotność iloczynu małych liczb pierwszych
i zauważyć, że wtedy wielokrotności tych liczb w każdym bloku są
położone tak samo.
liczby parzyste i użyć tablicy bitowej. Można również
przyjąć jako rozmiar bloku wielokrotność iloczynu małych liczb pierwszych
i zauważyć, że wtedy wielokrotności tych liczb w każdym bloku są
położone tak samo.