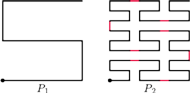
Rys. 1 Krzywa Peano rzędu powstaje z połączenia dziewięciu krzywych rzędu 
Od redakcji: czasami (np. na mathworld.wolfram.com) krzywa ta nazywana jest drugą krzywą Hilberta (ang. Hilbert II curve).

Nic więc dziwnego, że autorzy zadań na konkursach programistycznych chętnie sięgają po inspirację do świata fraktali. Jednym z popularnych typów zadań jest generowanie krzywych wypełniających płaszczyznę, np. krzywej Peano (zob. rysunek), Hilberta lub ich wariacji. 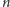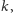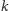Rozmiar takich krzywych rośnie wykładniczo względem rzędu krzywej, zatem zadanie zwykle jest formułowane następująco: dla krzywej rzędu  i liczby  stwierdzić, jakie współrzędne ma punkt płaszczyzny, leżący w odległości  od początku krzywej. Oczekuje się, że program będzie działać w czasie

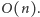
Najczęściej takie zadania nie są koncepcyjnie trudne. Przykładowo, gdybyśmy chcieli rozwiązać taki problem dla smoczej krzywej 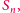 należy rozpatrzyć dwa przypadki:

(a)

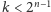 i wtedy rekurencyjnie znajdujemy rozwiązanie dla krzywej 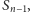  albo

(b)

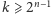 i wtedy znajdujemy punkt na krzywej 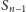  w odległości 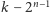 od początku krzywej i odpowiednio przesuwamy go na płaszczyźnie.

Dla krzywej Peano rozwiązanie jest analogiczne, z tym że trzeba będzie rozpatrzyć nie dwa, ale 9 przypadków.

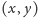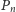Można jednak zadanie sformułować na odwrót: mając dany punkt płaszczyzny  leżący na krzywej, pytamy się, w jakiej odległości od początku krzywej się on znajduje. Takie zadanie dla krzywej Peano pojawiło się m.in. na światowych finałach konkursu ACM ICPC w roku 2003 (zadanie pt. Riding the Bus). Jego rozwiązanie także jest łatwe: krzywa Peano  rzędu 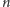 mieści się na kwadratowej siatce rozmiaru 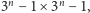 a jej długość to 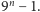  Patrząc na wartośc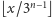i  i 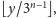 jesteśmy w stanie stwierdzić, do której z dziewięciu mniejszych krzywych 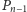 należy punkt 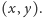 Jeśli należy do 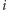-tej krzywej (w kolejności ich występowania w 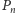), to wynikiem będzie suma 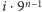 oraz rozwiązania podzadania dla krzywej 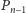 i punktu 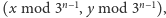 odpowiednio obróconego. Taki algorytm działa w czasie

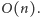
Odwrotny problem dla smoczej krzywej został postawiony przed uczestnikami tegorocznych Potyczek Algorytmicznych w zadaniu Ploter. Na pierwszy rzut oka wydaje się, że pomysł, którego użyliśmy dla krzywej Peano, tu się zupełnie nie sprawdzi. Brakuje nam bowiem istotnego składnika: jak dla punktu na krzywej 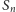 sprawdzić, do której z dwóch mniejszych krzywych 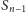 on należy. Spróbujmy więc trochę inaczej: wykonajmy procedurę rekurencyjnie dla obu mniejszych krzywych. Takie rozwiązanie działać będzie, oczywiście, w czasie 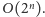 Ale zauważmy, że w wielu przypadkach, jeśli szukamy punktu na niewłaściwej krzywej mniejszego rzędu, to po kilku zejściach rekurencyjnych nasz punkt na tyle istotnie oddali się od aktualnie rozważanego kawałka krzywej, że będziemy mogli to łatwo wykryć i odciąć przeszukiwanie.

Zobaczmy, jak ta idea sprawdzi się w praktyce. Niech 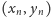 oznacza ostatni punkt na krzywej rzędu  Łatwo pokazać obliczającą go rekurencję :

Niech 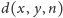 będzie funkcją, która zwraca zbiór odległości, w jakich punkt 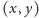 leży od początku krzywej 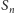 (dany punkt może leżeć w co najwyżej dwóch odległościach od początku krzywej). Funkcja ta wykona dwa wywołania rekurencyjne. Jej wynikiem będzie suma dwóch zbiorów:

Dla 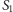 mamy

A kiedy możemy odciąć przeszukiwanie? Nie jesteśmy w stanie łatwo sprawdzić, czy dany punkt występuje na krzywej 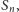 ale dla wielu punktów możemy powiedzieć, że na pewno na niej nie występują. 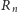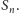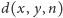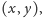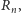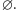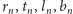Rozważmy bowiem najmniejszy prostokąt  o bokach równoległych do osi układu współrzędnych, który zawiera wszystkie punkty krzywej  Ilekroć funkcja  zostanie wywołana dla punktu  który leży poza prostokątem  możemy natychmiast zwrócić  Niech  oznaczają odległości punktu 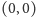 od krawędzi prostokąta 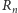 (odpowiednio prawej, górnej, lewej i dolnej). Możemy je obliczyć rekurencyjnie :

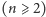Pozostało pytanie, na ile powyższa optymalizacja wpływa na czas działania algorYtmu. Narysujmy krzywą 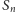 i zaznaczmy wszystkie prostokąty otaczające 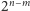 krzywych 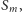 które składają się na krzywą 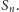 Oszacujmy, ile maksymalnie narysowanych prostokątów może zawierać dany punkt 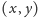; ta liczba będzie oznaczać, ile razy wywołanie 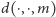 nie zostanie odcięte. Wynika z tego, że jeśli liczba prostokątów będzie rzędu 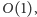 to na każdym poziomie rekurencji będziemy mieli stałą liczbę wywołań, a zatem cały algorytm będzie działał w czasie

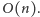
Można udowodnić przez indukcję, że 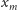 i 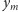 są podzielne przez 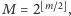 zatem każda z krzywych 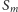 zaczyna się w jednym z punktów zbioru 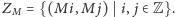 Można też pokazać, że 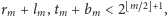 tak więc każdy z narysowanych prostokątów jest zawarty w kwadracie o boku 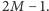 Zatem prostokąty zawierające punkt 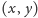 pokrywają w sumie co najwyżej 16 punktów ze zbioru 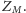 W każdym z tych punktów mogą zaczynać się co najwyżej cztery krzywe 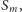 zatem 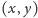 należy do nie więcej niż  prostokątów. Zatem nasz algorytm istotnie działa w czasie liniowym!