Jak wyznaczać wyrazy ciągu EKG?
Po przeczytaniu artykułu Marcina Pilipczuka trudno nie odnieść wrażenia, że nasz zasób wiedzy o zachowaniu ciągu EKG opiera się przede wszystkim na wynikach eksperymentów komputerowych, natomiast dowody otrzymanych w ten sposób hipotez pojawiają się z pewnym opóźnieniem.

Co więcej, niektóre własności nie doczekały się jeszcze ścisłych dowodów,
choć dane doświadczalne pokazują je na tyle wyraźnie, że ciężko byłoby
nie wierzyć w ich prawdziwość. Widzimy tu, że informatyka zaczyna
pełnić funkcję eksperymentalnej poddziedziny matematyki. Co ciekawe jednak,
nie chodzi tu tylko o łatwiejsze stawianie hipotez – wyniki obliczeń mogą
stanowić fragmenty dowodu odkrytych za ich pomocą własności!
W przypadku ciągu EKG przejawiło się to w automatycznym sprawdzeniu
prawdziwości hipotezy dla pewnej liczby początkowych wyrazów ciągu (dla
pozostałych zadziałało rozumowanie czysto matematyczne), ale zdarzały się już
w historii problemy, dla których cały dowód opierał się na komputerowej
analizie przypadków – na przykład dowód faktu, że każdą mapę (graf
planarny) można pokolorować czterema kolorami, tak aby żadne dwa
sąsiednie państwa (wierzchołki) nie miały tego samego koloru. Niektórzy
twierdzą, że takie rozumowanie, oparte w znacznej mierze na programach
komputerowych i często obszernych wynikach ich działania, nie jest właściwie
żadnym dowodem. Jest to argument poniekąd słuszny – ciężko ręcznie
zweryfikować poprawność tego typu wywodu. Ten medal ma jednak dwie
strony. Otóż przypomnijmy sobie chociażby liczne „dowody” Wielkiego
Twierdzenia Fermata, publikowane bez mała przez trzy stulecia, które
nie używały żadnych podejrzanych metod informatycznych, a mimo wszystko
okazywały się nieprawdziwe (niepełne). Czy autorzy tych „dowodów”
wierzyli w słuszność przedstawianych wyników? Podejrzewam, że tak.
Swoją drogą, zapewne większość Czytelników wierzy w prawdziwość
dowodu Andrew Wilesa, mimo iż jest on tak długi i skomplikowany, że
nie mieli ochoty go samodzielnie sprawdzić. Jeśli dołożymy do tego podobną
konkurencję rozgrywaną w obecnych czasach – próby odpowiedzi na słynne
pytanie:
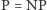 ?, jedno z fundamentalnych w informatyce teoretycznej,
których to prób – „dowodów” – były już dziesiątki (zainteresowany
Czytelnik znajdzie ich systematycznie aktualizowaną listę na stronie P versus NP)
– to zauważymy, że czysto matematyczne rozumowania wcale nie muszą być
lepsze i mniej błędogenne od rozumowań opartych na wynikach badań
eksperymentalnych.
?, jedno z fundamentalnych w informatyce teoretycznej,
których to prób – „dowodów” – były już dziesiątki (zainteresowany
Czytelnik znajdzie ich systematycznie aktualizowaną listę na stronie P versus NP)
– to zauważymy, że czysto matematyczne rozumowania wcale nie muszą być
lepsze i mniej błędogenne od rozumowań opartych na wynikach badań
eksperymentalnych.
W duchu powyższego, trochę przydługawego wstępu w tym artykule
zastanowimy się, jak efektywnie wyznaczać kolejne wyrazy ciągu EKG. Nasz
algorytm powinien być na tyle sprawny, aby dało się za jego pomocą
sprawdzić poprawność wyników eksperymentu Lagariasa, Rainsa
i Sloane’a, czyli powinien działać co najmniej dla indeksów około
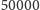 (w tych okolicach powinna pojawić się największa liczba pierwsza
mniejsza od
(w tych okolicach powinna pojawić się największa liczba pierwsza
mniejsza od
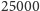 ). A im lepszy algorytm, tym lepiej pozwoli nam
badać asymptotykę ciągu EKG – a nuż uda się postawić kolejne ciekawe
hipotezy?
). A im lepszy algorytm, tym lepiej pozwoli nam
badać asymptotykę ciągu EKG – a nuż uda się postawić kolejne ciekawe
hipotezy?
Początek nie będzie zbyt odkrywczy: otóż metoda wyznaczania wyrazów
ciągu EKG
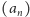 jest obecna implicite w tekście Marcina Pilipczuka.
Faktycznie, jeśli znamy
jest obecna implicite w tekście Marcina Pilipczuka.
Faktycznie, jeśli znamy
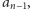 to wiemy, że jeden z dzielników
pierwszych tej liczby jest liczbą sterującą wyrazu
to wiemy, że jeden z dzielników
pierwszych tej liczby jest liczbą sterującą wyrazu
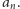 Jeśli właśnie liczba
pierwsza
Jeśli właśnie liczba
pierwsza
 jest tą liczbą sterującą, to
jest tą liczbą sterującą, to
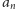 jest najmniejszą
wielokrotnością
jest najmniejszą
wielokrotnością
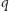 niewystępującą wcześniej w ciągu. Aby wśród
wszystkich dzielników pierwszych
niewystępującą wcześniej w ciągu. Aby wśród
wszystkich dzielników pierwszych
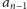 zidentyfikować liczbę
zidentyfikować liczbę
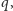 wystarczy, rzecz jasna, przejrzeć wszystkie te dzielniki i wybrać ten
o najmniejszej pierwszej wolnej wielokrotności.
wystarczy, rzecz jasna, przejrzeć wszystkie te dzielniki i wybrać ten
o najmniejszej pierwszej wolnej wielokrotności.
Aby uzupełnić ten opis postępowania, musimy wymyślić sposób efektywnego przejrzenia wszystkich dzielników pierwszych danej liczby naturalnej oraz sposób znalezienia najmniejszej wolnej wielokrotności każdego takiego dzielnika. Teraz zajmiemy się kolejno tymi dwiema lukami.
Problem rozkładu liczby naturalnej na czynniki pierwsze brzmi bardzo klasycznie: wydaje się, że powinien istnieć jakiś sympatyczny, efektywny algorytm dający sobie z nim radę. I faktycznie, jest to znany problem faktoryzacji liczby, lecz, niestety, w ogólności nie umiemy sobie z nim łatwo radzić – nie jest znany żaden wielomianowy algorytm rozwiązujący ten problem. Słowo wielomianowy oznacza tu algorytm o złożoności czasowej będącej jakimś wielomianem względem długości zapisu rozkładanej liczby, która to długość zapisu to mniej więcej logarytm z tej liczby.
Na szczęście, w naszej sytuacji nie musimy uciekać się do ogólnych
rozwiązań problemu faktoryzacji. Wystarczy, jeśli przypomnimy sobie, że
rozkładane przez nas liczby nie są zbyt duże, co w teorii wynika z górnego
oszacowania
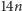 na wartość
na wartość
 -tego wyrazu ciągu, a w praktyce
z wykresu wartości pierwszych
-tego wyrazu ciągu, a w praktyce
z wykresu wartości pierwszych
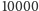 elementów ciągu zawartego
w artykule Marcina Pilipczuka.
elementów ciągu zawartego
w artykule Marcina Pilipczuka.
W przypadku tak niedużych liczb możemy użyć metody sita Eratostenesa. Podstawowa wersja tego algorytmu, służąca do wyznaczania kolejnych liczb pierwszych, jest na tyle znana, że w tym miejscu ograniczymy się do przypomnienia jej w postaci pseudokodu:
Obliczamy tu elementy boolowskiej tablicy pierwsza[2.. M], wykreślając
wielokrotności kolejnych liczb pierwszych, tj. oznaczając je jako liczby
złożone. Żeby było szybciej, przeglądanie wielokrotności liczby pierwszej
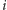 rozpoczynamy od
rozpoczynamy od
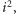 gdyż skądinąd wiemy, że wszystkie
mniejsze musiały już zostać wcześniej wykreślone. Na końcu mamy
zaznaczone (wartość true) wszystkie liczby pierwsze nie większe niż
gdyż skądinąd wiemy, że wszystkie
mniejsze musiały już zostać wcześniej wykreślone. Na końcu mamy
zaznaczone (wartość true) wszystkie liczby pierwsze nie większe niż
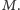 Zapewne nie wszyscy wiedzą, że ten sam algorytm można
wykorzystać także do rozkładania liczb na czynniki pierwsze. Wystarczy,
mianowicie, dołożyć dodatkową tablicę dzielnik[2..M], w której będziemy
przechowywać najmniejszy dzielnik pierwszy każdej liczby złożonej
z zakresu. Elementy tej tablicy inicjujemy na zera, a wypełniamy ją w momencie
wykreślania liczb, tzn. wewnątrz pętli while, za pomocą instrukcji:
Zapewne nie wszyscy wiedzą, że ten sam algorytm można
wykorzystać także do rozkładania liczb na czynniki pierwsze. Wystarczy,
mianowicie, dołożyć dodatkową tablicę dzielnik[2..M], w której będziemy
przechowywać najmniejszy dzielnik pierwszy każdej liczby złożonej
z zakresu. Elementy tej tablicy inicjujemy na zera, a wypełniamy ją w momencie
wykreślania liczb, tzn. wewnątrz pętli while, za pomocą instrukcji:
Za pomocą tablicy dzielnik możemy już łatwo faktoryzować liczby
nieprzekraczające
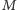 : dla danej liczby
: dla danej liczby
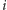 jako pierwszy podajemy
dzielnik dzielnik[i], następnie dzielnik[i/dzielnik[i]] i tak dalej, aż dojdziemy
do jedynki. Takich kroków wykonamy nie więcej niż
jako pierwszy podajemy
dzielnik dzielnik[i], następnie dzielnik[i/dzielnik[i]] i tak dalej, aż dojdziemy
do jedynki. Takich kroków wykonamy nie więcej niż
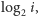 gdyż za
każdym razem
gdyż za
każdym razem
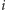 zmniejszamy co najmniej dwukrotnie. Dzięki temu, że
w tablicy pamiętamy najmniejsze dzielniki pierwsze liczb, uzyskana w tym
postępowaniu lista dzielników będzie zawsze niemalejąca, więc łatwo usuniemy
z niej powtórzenia.
zmniejszamy co najmniej dwukrotnie. Dzięki temu, że
w tablicy pamiętamy najmniejsze dzielniki pierwsze liczb, uzyskana w tym
postępowaniu lista dzielników będzie zawsze niemalejąca, więc łatwo usuniemy
z niej powtórzenia.
Stosując podobny argument (do tego z logarytmem), można wykazać, że
złożoność czasowa sita Eratostenesa to
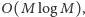 co pozostawiamy
Czytelnikowi (tak naprawdę złożoność tę można oszacować nawet przez
co pozostawiamy
Czytelnikowi (tak naprawdę złożoność tę można oszacować nawet przez
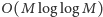 ). Jeśli przypomnimy sobie, iż
). Jeśli przypomnimy sobie, iż
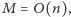 przy
czym
przy
czym
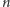 to indeks wyrazu ciągu EKG, który chcemy obliczyć, to słusznie
zauważymy, że z problemem faktoryzacji poradziliśmy już sobie całkiem
sprawnie.
to indeks wyrazu ciągu EKG, który chcemy obliczyć, to słusznie
zauważymy, że z problemem faktoryzacji poradziliśmy już sobie całkiem
sprawnie.
Do zakończenia opisu całego algorytmu pozostała nam już tylko kwestia wyznaczania najmniejszych wolnych wielokrotności poszczególnych liczb pierwszych z rozkładu. Z tą częścią rozwiązania możemy poradzić sobie całkiem prosto, o ile zastosujemy odpowiednio sprytną strukturę danych, przy czym nie będzie to wcale struktura wysublimowana.
Znów skorzystamy z tego, że zakres interesujących nas liczb pierwszych
jest nieduży. Dla każdej liczby pierwszej
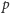 nie większej niż
nie większej niż
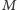 będziemy przechowywać, jako wiel, jakąś wielokrotność liczby
będziemy przechowywać, jako wiel, jakąś wielokrotność liczby
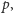 która wystąpiła już w ciągu. Zadbamy o to, aby w algorytmie
jedynie powiększać te wartości, aktualizując je tylko w razie potrzeby.
Początkowo wiel[p]=0. Dodatkowo, w tablicy boolowskiej użyte[0..M]
będziemy pamiętali informację o tym, które liczby wystąpiły już w ciągu EKG.
Początkowo, dla wygody, ustawiamy użyte[0]= true, a resztę komórek na
false. Okazuje się, że to już wystarczy – poniżej pseudokod wyznaczania
najmniejszej wolnej wielokrotności liczby
która wystąpiła już w ciągu. Zadbamy o to, aby w algorytmie
jedynie powiększać te wartości, aktualizując je tylko w razie potrzeby.
Początkowo wiel[p]=0. Dodatkowo, w tablicy boolowskiej użyte[0..M]
będziemy pamiętali informację o tym, które liczby wystąpiły już w ciągu EKG.
Początkowo, dla wygody, ustawiamy użyte[0]= true, a resztę komórek na
false. Okazuje się, że to już wystarczy – poniżej pseudokod wyznaczania
najmniejszej wolnej wielokrotności liczby
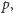 w którym, w gruncie
rzeczy, nic się nie dzieje.
w którym, w gruncie
rzeczy, nic się nie dzieje.
Powyższa pętla może i wygląda bardzo nieoptymalnie, ale nie jest
w rzeczywistości taka zła. Otóż wystarczy zauważyć, że dana liczba
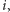
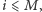 może wystąpić jako wiel[p] dla nie więcej niż
może wystąpić jako wiel[p] dla nie więcej niż
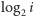 liczb pierwszych
liczb pierwszych
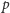 (będą to, oczywiście, dzielniki pierwsze
liczby
(będą to, oczywiście, dzielniki pierwsze
liczby
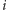 ). To oznacza, że łączna liczba obrotów powyższej pętli
while z pewnością nie przekroczy
). To oznacza, że łączna liczba obrotów powyższej pętli
while z pewnością nie przekroczy
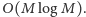 Możemy już
podsumować cały algorytm wyznaczania
Możemy już
podsumować cały algorytm wyznaczania
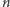 -tego wyrazu ciągu
EKG. Używamy w nim zaledwie czterech tablic rozmiaru co najwyżej
-tego wyrazu ciągu
EKG. Używamy w nim zaledwie czterech tablic rozmiaru co najwyżej
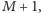 przy czym dwie z nich ( pierwsza i dzielnik) wypełniamy na
samym początku w czasie
przy czym dwie z nich ( pierwsza i dzielnik) wypełniamy na
samym początku w czasie
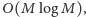 a dwie pozostałe ( wiel i użyte)
uzupełniamy w trakcie obliczania kolejnych wyrazów ciągu EKG, również
w łącznym czasie
a dwie pozostałe ( wiel i użyte)
uzupełniamy w trakcie obliczania kolejnych wyrazów ciągu EKG, również
w łącznym czasie
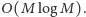 W takim samym czasie możemy
wyznaczyć wszystkie dzielniki pierwsze wszystkich liczb z podanego zakresu.
Stąd całe rozwiązanie działa w czasie
W takim samym czasie możemy
wyznaczyć wszystkie dzielniki pierwsze wszystkich liczb z podanego zakresu.
Stąd całe rozwiązanie działa w czasie
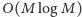 i w pamięci
i w pamięci
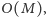 przy czym
przy czym
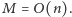 Algorytm szybki, a zarazem prosty
– i o to w tym sporcie chodzi.
Algorytm szybki, a zarazem prosty
– i o to w tym sporcie chodzi.
Można by jednak spytać, czy nie da się lepiej. W szczególności, w podanej
metodzie przy wyznaczaniu
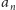 musimy najpierw obliczyć wszystkie
wcześniejsze wyrazy ciągu EKG – a może dałoby się obejść szybciej i bez
tego? Podobnie jak Lagarias, Rains i Sloane, którzy w swojej pracy opisują
algorytm zbliżony do powyższego, autor tego artykułu nie zna odpowiedzi na
to pytanie, ale może Czytelnik ma jakiś pomysł? Jeśli tak, zachęcamy do
podzielenia się nim z Redakcją.
musimy najpierw obliczyć wszystkie
wcześniejsze wyrazy ciągu EKG – a może dałoby się obejść szybciej i bez
tego? Podobnie jak Lagarias, Rains i Sloane, którzy w swojej pracy opisują
algorytm zbliżony do powyższego, autor tego artykułu nie zna odpowiedzi na
to pytanie, ale może Czytelnik ma jakiś pomysł? Jeśli tak, zachęcamy do
podzielenia się nim z Redakcją.
 ;
; 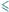 M
M