Informatyczny kącik olimpijski
Trening
Tym razem przyjrzymy się zadaniu Training z Międzynarodowej Olimpiady Informatycznej 2007.
Zadanie. Mamy dany spójny graf nieskierowany o
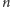 wierzchołkach
z wyróżnionym drzewem rozpinającym (tzn.
wyróżnione jest
wierzchołkach
z wyróżnionym drzewem rozpinającym (tzn.
wyróżnione jest
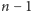 krawędzi, które tworzą drzewo). Krawędzie
spoza tego drzewa mają przypisane koszty. Należy przeciąć krawędzie
o najmniejszej sumie kosztów, tak aby w grafie nie pozostał żaden cykl
prosty (tzn. taki, w którym nie powtarzają się wierzchołki) długości
parzystej. Krawędzi drzewowych nie wolno przecinać. Dodatkowo wiadomo,
że stopień żadnego z wierzchołków grafu nie przekracza (niedużego)
krawędzi, które tworzą drzewo). Krawędzie
spoza tego drzewa mają przypisane koszty. Należy przeciąć krawędzie
o najmniejszej sumie kosztów, tak aby w grafie nie pozostał żaden cykl
prosty (tzn. taki, w którym nie powtarzają się wierzchołki) długości
parzystej. Krawędzi drzewowych nie wolno przecinać. Dodatkowo wiadomo,
że stopień żadnego z wierzchołków grafu nie przekracza (niedużego)
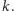
Krawędzie spoza drzewa będę nazywał poprzecznymi. Każda poprzeczna
krawędź tworzy z naszym drzewem dokładnie jeden cykl (nazwijmy go cyklem
poprzecznym). Jeśli cykl ten jest długości parzystej, musimy tę krawędź
przeciąć, robimy więc to czym prędzej i nie zajmujemy się więcej taką
krawędzią. Zauważmy, że w poprawnym rozwiązaniu możemy pozostawić
cykle poprzeczne długości nieparzystej, ale tylko pod warunkiem, że żadne
dwa z nich nie mają wspólnej krawędzi. Gdyby bowiem miały, to przez ich
złączenie i usunięcie części wspólnej uzyskalibyśmy cykl prosty długości
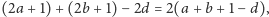 przy czym
przy czym
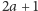 i
i
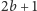 są długościami tych cykli, a
są długościami tych cykli, a
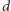 – długością części
wspólnej. Cykli poprzecznych bez wspólnych krawędzi nie da się w żaden
sposób połączyć w cykl prosty. Zadanie sprowadza się więc do wybrania
poprzecznych krawędzi, które możemy pozostawić, tak aby odpowiadające im
cykle poprzeczne nie miały wspólnych krawędzi.
– długością części
wspólnej. Cykli poprzecznych bez wspólnych krawędzi nie da się w żaden
sposób połączyć w cykl prosty. Zadanie sprowadza się więc do wybrania
poprzecznych krawędzi, które możemy pozostawić, tak aby odpowiadające im
cykle poprzeczne nie miały wspólnych krawędzi.
Do rozwiązania tak uproszczonego problemu użyjemy programowania
dynamicznego. Ukorzeńmy nasze drzewo rozpinające. Dla każdego
wierzchołka
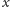 i dla każdego podzbioru
i dla każdego podzbioru
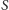 synów
synów
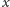 w naszym drzewie obliczymy
w naszym drzewie obliczymy
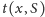 – największą możliwą sumę
kosztów poprzecznych krawędzi, które możemy pozostawić, a których
cykle są rozłączne krawędziowo i zawierają się całkowicie w podgrafie
złożonym z krawędzi łączących
– największą możliwą sumę
kosztów poprzecznych krawędzi, które możemy pozostawić, a których
cykle są rozłączne krawędziowo i zawierają się całkowicie w podgrafie
złożonym z krawędzi łączących
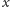 z wierzchołkami z
z wierzchołkami z
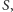 poddrzew
wierzchołków z
poddrzew
wierzchołków z
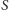 oraz poprzecznych krawędzi.
oraz poprzecznych krawędzi.
Aby obliczyć
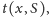 musimy zastanowić się nad cyklami
poprzecznymi, które przechodzą przez
musimy zastanowić się nad cyklami
poprzecznymi, które przechodzą przez
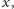 ale nie przechodzą przez ojca
ale nie przechodzą przez ojca
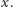 Jeśli
Jeśli
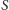 jest pusty, to
jest pusty, to
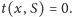 W przeciwnym
przypadku ustalmy pierwszego syna
W przeciwnym
przypadku ustalmy pierwszego syna
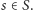 Załóżmy, że istnieje cykl
poprzeczny, który zawiera
Załóżmy, że istnieje cykl
poprzeczny, który zawiera
 i
i
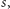 ale nie zawiera ojca
ale nie zawiera ojca
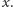 Niech
Niech
 będzie krawędzią poprzeczną tegoż cyklu, a
będzie krawędzią poprzeczną tegoż cyklu, a
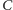 – zbiorem
jego wierzchołków. Wtedy przy obliczaniu
– zbiorem
jego wierzchołków. Wtedy przy obliczaniu
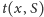 należy uwzględnić
wyrażenie:
należy uwzględnić
wyrażenie:
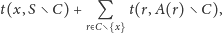 | (1) |
przy czym
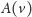 oznacza zbiór wszystkich synów wierzchołka
oznacza zbiór wszystkich synów wierzchołka
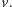 Możemy też nie zdecydować się wziąć żadnego takiego cyklu, czemu
odpowiada wyrażenie:
Możemy też nie zdecydować się wziąć żadnego takiego cyklu, czemu
odpowiada wyrażenie:
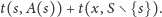 | (2) |
Ostatecznie jako
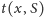 weźmiemy maksimum z wartości (1) po
odpowiednich parach
weźmiemy maksimum z wartości (1) po
odpowiednich parach
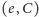 oraz (2).
oraz (2).
Odpowiedzią w naszym zadaniu będzie

przy czym
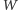 jest sumą kosztów wszystkich krawędzi poprzecznych, a
jest sumą kosztów wszystkich krawędzi poprzecznych, a
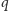 – korzeniem drzewa.
– korzeniem drzewa.
Zastanówmy się nad złożonością czasową tego rozwiązania. Graf ma
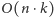 krawędzi. Dla każdej krawędzi poprzecznej musimy znaleźć
jej cykl w czasie
krawędzi. Dla każdej krawędzi poprzecznej musimy znaleźć
jej cykl w czasie
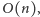 co daje łączny koszt
co daje łączny koszt
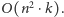 Każda
krawędź poprzeczna
Każda
krawędź poprzeczna
 jest rozważana podczas programowania
dynamicznego tylko dla wierzchołka
jest rozważana podczas programowania
dynamicznego tylko dla wierzchołka
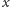 będącego najwyższym
wierzchołkiem w drzewie, do którego sięga cykl poprzeczny zawierający
będącego najwyższym
wierzchołkiem w drzewie, do którego sięga cykl poprzeczny zawierający
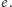 Stąd sumę po wierzchołkach tego cyklu, występującą w wyrażeniu (1),
wystarczy obliczyć raz. Dla każdej pary
Stąd sumę po wierzchołkach tego cyklu, występującą w wyrażeniu (1),
wystarczy obliczyć raz. Dla każdej pary
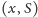 wybieramy albo brak
krawędzi poprzecznych, albo też jedną z krawędzi, których cykle przechodzą
przez
wybieramy albo brak
krawędzi poprzecznych, albo też jedną z krawędzi, których cykle przechodzą
przez
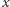 oraz pierwszego syna
oraz pierwszego syna
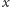 w
w
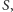 ale nie przez ojca
ale nie przez ojca
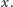 Niech takich właśnie krawędzi poprzecznych będzie
Niech takich właśnie krawędzi poprzecznych będzie
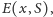 a wszystkich krawędzi, których cykle przechodzą przez
a wszystkich krawędzi, których cykle przechodzą przez
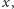 ale
nie przechodzą przez jego ojca –
ale
nie przechodzą przez jego ojca –
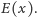 Wtedy
Wtedy
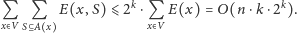 |
Programowanie dynamiczne zajmuje więc czas
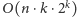 plus
obliczanie sum po wstawianych cyklach, którego koszt czasowy jest taki
sam jak koszt szukania tych cykli. Stąd łączna złożoność czasowa to
plus
obliczanie sum po wstawianych cyklach, którego koszt czasowy jest taki
sam jak koszt szukania tych cykli. Stąd łączna złożoność czasowa to
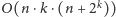 przy zużyciu pamięci rzędu
przy zużyciu pamięci rzędu