Informatyczny kącik olimpijski
Zapotrzebowanie na prąd
W tym kąciku spróbujemy rozwiązać zadanie Electric needs pochodzące z drużynowych zawodów studenckich z serii ACM ICPC, a konkretnie z mistrzostw Ameryki Łacińskiej 2010.
Zadanie. Rozważmy prostokątny obszar
podzielony na kwadraty jednostkowe, w którym kolumny ponumerowane
są od
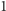 do
do
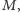 a wiersze od
a wiersze od
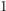 do
do
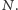 Każdy
kwadrat jednostkowy reprezentuje działkę, która może być zajęta przez
budynek lub nie. Na dokładnie
Każdy
kwadrat jednostkowy reprezentuje działkę, która może być zajęta przez
budynek lub nie. Na dokładnie
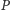 działkach, których współrzędne
mamy podane, znajdują
się budynki elektrowni. Wszystkie pozostałe pola są uszeregowane wedle swej
wartości dla przedsiębiorców. Pola położone bliżej elektrowni są bardziej
wartościowe od wszystkich odleglejszych (bierzemy pod uwagę odległość
od najbliższego pola zajętego przez elektrownię w metryce maksimum, tzn.
działkach, których współrzędne
mamy podane, znajdują
się budynki elektrowni. Wszystkie pozostałe pola są uszeregowane wedle swej
wartości dla przedsiębiorców. Pola położone bliżej elektrowni są bardziej
wartościowe od wszystkich odleglejszych (bierzemy pod uwagę odległość
od najbliższego pola zajętego przez elektrownię w metryce maksimum, tzn.
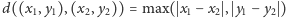 ).
W przypadku jednakowej odległości od elektrowni za bardziej wartościowe
uznajemy pola z wierszy o mniejszych numerach, a gdy także to kryterium
nie jest rozstrzygające – z kolumn o mniejszych numerach. Naszym zadaniem
jest odpowiedzieć na
).
W przypadku jednakowej odległości od elektrowni za bardziej wartościowe
uznajemy pola z wierszy o mniejszych numerach, a gdy także to kryterium
nie jest rozstrzygające – z kolumn o mniejszych numerach. Naszym zadaniem
jest odpowiedzieć na
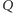 zapytań postaci: „podaj współrzędne pola,
które jest
zapytań postaci: „podaj współrzędne pola,
które jest
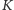 -te z kolei na liście najbardziej wartościowych”.
-te z kolei na liście najbardziej wartościowych”.
Naturalnym podejściem jest wyznaczenie odległości każdego pola od
elektrowni. Można to zrobić, budując graf nieskierowany, którego
wierzchołkami są nasze pola, a krawędzie łączą pola sąsiadujące bokiem lub
rogiem. W takim grafie wystarczy wykonać jedno przeszukiwanie wszerz (BFS),
startując ze wszystkich pól elektrowni naraz. Zachęcamy Czytelnika, aby
zastanowił się, dlaczego odległość w takim grafie jest równoważna
odległości w metryce maksimum. Obliczywszy wszystkie odległości,
sortujemy pola według kryteriów podanych w zadaniu, a na każde
zapytanie odpowiadamy, po prostu podając współrzędne
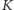 -tego pola
z posortowanej listy. Daje to łącznie
-tego pola
z posortowanej listy. Daje to łącznie
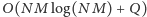 operacji albo
nawet
operacji albo
nawet
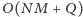 operacji, jeśli sortowanie wykonamy metodą
kubełkową. Prawdopodobnie byłby to najlepszy sposób postępowania, gdyby nie
fakt, że w tym zadaniu górne ograniczenia na
operacji, jeśli sortowanie wykonamy metodą
kubełkową. Prawdopodobnie byłby to najlepszy sposób postępowania, gdyby nie
fakt, że w tym zadaniu górne ograniczenia na
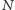 i
i
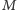 są dużo
większe niż na
są dużo
większe niż na
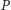 i
i
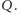 Innymi słowy, szukamy rozwiązania,
którego złożoność będzie zależała bardziej od
Innymi słowy, szukamy rozwiązania,
którego złożoność będzie zależała bardziej od
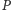 i
i
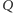 niż
niż
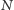 czy
czy
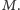
W takim razie zastanówmy się najpierw, w jakiej odległości od najbliższej
elektrowni położone jest szukane,
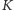 -te pole. Nie widać sposobu na
obliczenie tego wprost, spróbujmy wyszukać wynik binarnie. W tym celu
potrzebujemy metody sprawdzania, ile jest pól, których odległość od elektrowni
wynosi co najwyżej
-te pole. Nie widać sposobu na
obliczenie tego wprost, spróbujmy wyszukać wynik binarnie. W tym celu
potrzebujemy metody sprawdzania, ile jest pól, których odległość od elektrowni
wynosi co najwyżej
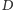 – za jej pomocą wyszukamy najmniejszą
wartość
– za jej pomocą wyszukamy najmniejszą
wartość
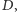 taką że tych pól jest co najmniej
taką że tych pól jest co najmniej
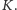 Zauważmy,
że pola, których odległość od ustalonego pola elektrowni wynosi co
najwyżej
Zauważmy,
że pola, których odległość od ustalonego pola elektrowni wynosi co
najwyżej
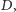 tworzą kwadrat o boku
tworzą kwadrat o boku
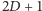 (kwadrat może być
ucięty, jeśli wystaje poza planszę) i środku w elektrowni. Stąd musimy
obliczyć, ile pól łącznie zajmuje
(kwadrat może być
ucięty, jeśli wystaje poza planszę) i środku w elektrowni. Stąd musimy
obliczyć, ile pól łącznie zajmuje
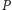 takich kwadratów (względnie
prostokątów). Tym problemem zajmiemy się za chwilę, póki co spójrzmy, jak
ma się to do rozwiązania całego zadania. Jeśli znamy już odległość
takich kwadratów (względnie
prostokątów). Tym problemem zajmiemy się za chwilę, póki co spójrzmy, jak
ma się to do rozwiązania całego zadania. Jeśli znamy już odległość
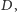 obliczamy najpierw, ile jest pól w odległości co najwyżej
obliczamy najpierw, ile jest pól w odległości co najwyżej
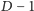 od elektrowni, odejmujemy tę liczbę od
od elektrowni, odejmujemy tę liczbę od
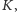 uzyskując nowy
parametr
uzyskując nowy
parametr
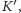 i rozwiązujemy powstały problem: które z pól
odległych od najbliższej elektrowni o dokładnie
i rozwiązujemy powstały problem: które z pól
odległych od najbliższej elektrowni o dokładnie
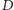 jest na pozycji
jest na pozycji
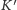 -tej na liście tychże pól w zadanej kolejności. Zacznijmy
od ustalenia, w którym wierszu jest nasz
-tej na liście tychże pól w zadanej kolejności. Zacznijmy
od ustalenia, w którym wierszu jest nasz
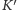 -ty element. Znów
nie widać sposobu na obliczenie tego wprost, więc decydujemy się na
wyszukiwanie binarne. Potrzebujemy odpowiedzi na pytanie: „ile jest pól
odległych od najbliższej elektrowni o dokładnie
-ty element. Znów
nie widać sposobu na obliczenie tego wprost, więc decydujemy się na
wyszukiwanie binarne. Potrzebujemy odpowiedzi na pytanie: „ile jest pól
odległych od najbliższej elektrowni o dokładnie
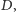 które znajdują
się w pierwszych
które znajdują
się w pierwszych
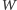 wierszach?”. Naturalnie, będziemy szukali
najmniejszego takiego
wierszach?”. Naturalnie, będziemy szukali
najmniejszego takiego
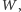 że odpowiedź na to pytanie jest nie
mniejsza niż
że odpowiedź na to pytanie jest nie
mniejsza niż
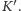 Problem jest podobny do poprzedniego. Tym
razem jednak odległość dokładnie
Problem jest podobny do poprzedniego. Tym
razem jednak odległość dokładnie
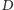 od najbliższej elektrowni
oznacza pola zawarte w kwadracie o boku
od najbliższej elektrowni
oznacza pola zawarte w kwadracie o boku
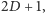 ale niezawarte
w kwadracie o boku
ale niezawarte
w kwadracie o boku
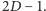 Kwadraty te trzeba obcinać odpowiednio
do prostokątów, jeśli wystają poza planszę (która ma teraz wymiary
Kwadraty te trzeba obcinać odpowiednio
do prostokątów, jeśli wystają poza planszę (która ma teraz wymiary
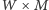 ). Ponieważ wszystkie mniejsze kwadraty zawierają się
w większych, więc wystarczy obliczyć łączne pole sumy większych i odjąć od
niego pole sumy mniejszych. Tak więc ponownie sprowadziliśmy problem do
obliczenia pola sumy prostokątów. Na koniec pozostaje ustalić, które
dokładnie z pól w danym wierszu należy wybrać. W tym celu od
). Ponieważ wszystkie mniejsze kwadraty zawierają się
w większych, więc wystarczy obliczyć łączne pole sumy większych i odjąć od
niego pole sumy mniejszych. Tak więc ponownie sprowadziliśmy problem do
obliczenia pola sumy prostokątów. Na koniec pozostaje ustalić, które
dokładnie z pól w danym wierszu należy wybrać. W tym celu od
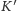 odejmujemy liczbę pól w odległości dokładnie
odejmujemy liczbę pól w odległości dokładnie
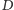 od
elektrowni, które znajdują się w wierszach o numerach od
od
elektrowni, które znajdują się w wierszach o numerach od
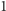 do
do
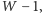 otrzymując w ten sposób nowy parametr
otrzymując w ten sposób nowy parametr
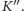 Następnie
w identyczny sposób wyszukujemy binarnie minimalne takie
Następnie
w identyczny sposób wyszukujemy binarnie minimalne takie
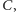 żeby
w pierwszych
żeby
w pierwszych
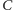 kolumnach wiersza o numerze
kolumnach wiersza o numerze
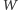 było co
najmniej
było co
najmniej
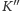 pól o odległości od elektrowni równej
pól o odległości od elektrowni równej
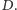 Dla
danego
Dla
danego
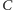 wystarczy obciąć kwadraty o bokach
wystarczy obciąć kwadraty o bokach
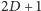 i
i
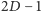 do żądanej części wiersza o numerze
do żądanej części wiersza o numerze
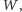 a potem
obliczyć różnicę sum pól powstałych prostokątów o jednym boku
długości 1.
a potem
obliczyć różnicę sum pól powstałych prostokątów o jednym boku
długości 1.
Sprowadziliśmy zatem cały problem do obliczenia pola sumy
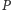 prostokątów
prostokątów
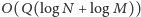 razy. Można ten problem rozwiązać dość
prosto w czasie
razy. Można ten problem rozwiązać dość
prosto w czasie
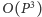 lub
lub
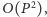 co było wystarczające w tym
zadaniu (opracowanie takich rozwiązań pozostawiamy Czytelnikowi).
Istnieje też efektywniejsze rozwiązanie, w złożoności czasowej
co było wystarczające w tym
zadaniu (opracowanie takich rozwiązań pozostawiamy Czytelnikowi).
Istnieje też efektywniejsze rozwiązanie, w złożoności czasowej
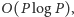 wykorzystujące technikę zamiatania oraz drzewo przedziałowe,
w którym w każdym węźle pamiętamy dodatkowo długość sumy
przedziałów w jego poddrzewie. Szczegóły tego rozwiązania pomijamy,
można o nim posłuchać na stronie http:/was.zaa.mimuw.edu.pl/?q=node/37,
poczytać w książce Preparaty i Shamosa Geometria obliczeniowa.
Wprowadzenie albo, najlepiej, wymyślić je samemu.
wykorzystujące technikę zamiatania oraz drzewo przedziałowe,
w którym w każdym węźle pamiętamy dodatkowo długość sumy
przedziałów w jego poddrzewie. Szczegóły tego rozwiązania pomijamy,
można o nim posłuchać na stronie http:/was.zaa.mimuw.edu.pl/?q=node/37,
poczytać w książce Preparaty i Shamosa Geometria obliczeniowa.
Wprowadzenie albo, najlepiej, wymyślić je samemu.
Rozwiązanie całego zadania wymaga zatem
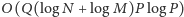 operacji.
operacji.