Mała Delta
O rozgrywkach ligowych
W sporcie stosowane są różne systemy prowadzenia rozgrywek. Jednym z nich jest tzw. system pucharowy, w którym zwycięzca meczu kwalifikuje się do dalszych gier, przegrany zaś odpada z turnieju. Aby system był bardziej sprawiedliwy, dokonuje się początkowego rozstawienia przeciwników, tak by teoretycznie najsilniejsi spotkali się jak najpóźniej.
Innym systemem, bardzo przydatnym, gdy nie mamy danego rankingu drużyn,
jest tzw. system kołowy, bardziej znany po prostu jako rozgrywki ligowe.
W systemie tym mamy
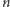 drużyn i każda rozgrywa mecz ze wszystkimi
pozostałymi – dzięki temu jest to bardzo sprawiedliwy system. Łącznie
mamy
drużyn i każda rozgrywa mecz ze wszystkimi
pozostałymi – dzięki temu jest to bardzo sprawiedliwy system. Łącznie
mamy
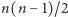 meczów. Rozgrywki składają się z kolejek. Jeśli
meczów. Rozgrywki składają się z kolejek. Jeśli
 jest parzyste, to w każdej kolejce uczestniczą wszystkie drużyny,
a jeśli nieparzyste, to jedna drużyna pauzuje. Drugi przypadek możemy
sprowadzić do pierwszego, dorzucając fikcyjną drużynę i interpretując
pauzowanie jako wygrany z nią mecz. Każda drużyna musi rozegrać
jest parzyste, to w każdej kolejce uczestniczą wszystkie drużyny,
a jeśli nieparzyste, to jedna drużyna pauzuje. Drugi przypadek możemy
sprowadzić do pierwszego, dorzucając fikcyjną drużynę i interpretując
pauzowanie jako wygrany z nią mecz. Każda drużyna musi rozegrać
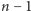 meczów, a więc liczba kolejek musi być równa co najmniej tyle.
Jeśli spojrzymy na terminarze spotkań różnych lig, to zobaczymy, że
składają się one właśnie z tylu kolejek. Ale dlaczego? Dlaczego zawsze
udaje się tak ułożyć terminarz, aby nie zdarzyła się sytuacja, w której
wypada, że dane dwie drużyny, które już grały ze sobą, teraz znowu
miałyby na siebie trafić? Czy jest to możliwe dla dowolnej parzystej liczby
drużyn?
meczów, a więc liczba kolejek musi być równa co najmniej tyle.
Jeśli spojrzymy na terminarze spotkań różnych lig, to zobaczymy, że
składają się one właśnie z tylu kolejek. Ale dlaczego? Dlaczego zawsze
udaje się tak ułożyć terminarz, aby nie zdarzyła się sytuacja, w której
wypada, że dane dwie drużyny, które już grały ze sobą, teraz znowu
miałyby na siebie trafić? Czy jest to możliwe dla dowolnej parzystej liczby
drużyn?
Popatrzmy na przykłady z życia. Czy jesteśmy w stanie znaleźć dla dowolnej (odpowiednio małej) parzystej wartości ligę o takiej liczbie drużyn? Poszukajmy wśród lig piłki nożnej:
- 2–
- to dość trywialny przypadek – mecz pomiędzy dwiema drużynami, trudno to nawet nazwać ligą,
- 4–
- przykładowo rozgrywki grupowe w finałach Mistrzostw Świata albo Europy, rozgrywki grupowe Ligi Mistrzów; bardzo często łączone z systemem pucharowym (najpierw faza grupowa, potem pucharowa),
- 6–
- np. finałowa runda eliminacji do Mistrzostw Świata w strefie obejmującej Amerykę Północną i Środkową ( CONCACAF), do niedawna taką wielkość miały grupy w rozgrywkach Ligi Europejskiej pod warunkiem, że pauzowanie interpretujemy jako mecz z fikcyjną drużyną (grupy w rzeczywistości liczyły po 5 drużyn),
- 8–
- trudno znaleźć ligę o tej liczbie drużyn, ale liga polska w sezonie 2001/02 była podzielona na dwie grupy po 8 drużyn, z których następnie po cztery najlepsze drużyny wchodziły do grupy mistrzowskiej, a pozostałe do grupy spadkowej,
- 10–
- np. liga austriacka, słoweńska, szwajcarska czy grupa eliminacyjna do Mistrzostw Świata w Ameryce Południowej ( CONMEBOL),
- 12–
- np. liga duńska, szkocka, słowacka,
- 14–
- tyle drużyn liczyła liga polska w sezonach 2003/04 i 2004/05,
- 16–
- typowa wielkość dla większości lig europejskich, np. liga belgijska, bułgarska, czeska, fińska, grecka, norweska, polska, portugalska, rosyjska,
- 18–
- np. niemiecka Bundesliga, liga holenderska, rumuńska, turecka,
- 20–
- typowa obecnie wielkość dla najlepszych lig europejskich, takich jak angielska Premier League, francuska Ligue 1, hiszpańska Primera División, włoska Serie A; również liga argentyńska czy brazylijska,
- 24–
- np. angielska „druga liga” – Championship.
Dla wszystkich wymienionych lig, aby każda drużyna zagrała z każdą,
wystarcza
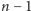 kolejek. Skłania nas to do przypuszczenia, że dla
dowolnej liczby parzystej
kolejek. Skłania nas to do przypuszczenia, że dla
dowolnej liczby parzystej
 w lidze liczącej
w lidze liczącej
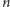 drużyn zawsze da
się tak ułożyć terminarz spotkań, żeby do rozegrania wszystkich meczów
wystarczyło
drużyn zawsze da
się tak ułożyć terminarz spotkań, żeby do rozegrania wszystkich meczów
wystarczyło
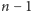 kolejek.
kolejek.
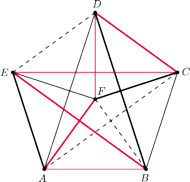
Rys. 1
Spróbujmy to przetłumaczyć na nieco inny język: przedstawimy rozgrywki jako
graf. Wierzchołkami będą drużyny danej ligi (zakładamy, że liczba
wierzchołków
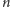 jest parzysta), a krawędź łącząca dwa wierzchołki
będzie oznaczała mecz między odpowiednimi drużynami. Każde dwie
drużyny mają ze sobą grać, więc rysujemy wszystkie możliwe krawędzie – taki
graf to graf pełny albo klika o
jest parzysta), a krawędź łącząca dwa wierzchołki
będzie oznaczała mecz między odpowiednimi drużynami. Każde dwie
drużyny mają ze sobą grać, więc rysujemy wszystkie możliwe krawędzie – taki
graf to graf pełny albo klika o
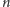 wierzchołkach. Będziemy kolorować
krawędzie naszego grafu
wierzchołkach. Będziemy kolorować
krawędzie naszego grafu
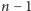 kolorami. Kolory oznaczają kolejki,
w których odbywają się mecze. Chcemy tak pokolorować krawędzie, aby
z każdego wierzchołka wychodziła krawędź każdego koloru i każdym
kolorem było pokolorowane
kolorami. Kolory oznaczają kolejki,
w których odbywają się mecze. Chcemy tak pokolorować krawędzie, aby
z każdego wierzchołka wychodziła krawędź każdego koloru i każdym
kolorem było pokolorowane
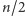 krawędzi. Jeśli to się uda, to fachowo
mówimy, że
krawędzi. Jeśli to się uda, to fachowo
mówimy, że
graf pełny ( klika) o
 wierzchołkach rozkłada się na
wierzchołkach rozkłada się na
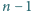 doskonałych skojarzeń.
doskonałych skojarzeń.
Jak wykazać, że dla dowolnej liczby parzystej
 można tak
pokolorować krawędzie grafu pełnego? Okazuje się, że można to zrobić
w bardzo sprytny i przejrzysty sposób. Co więcej, będzie to sposób
konstruktywny! Umieśćmy mianowicie
można tak
pokolorować krawędzie grafu pełnego? Okazuje się, że można to zrobić
w bardzo sprytny i przejrzysty sposób. Co więcej, będzie to sposób
konstruktywny! Umieśćmy mianowicie
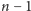 drużyn w wierzchołkach
drużyn w wierzchołkach
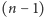 -kąta foremnego, a ostatnią w jego środku, tak jak na rysunku 1
(zamiast różnych kolorów są różne rodzaje linii). Teraz sprawa jest
dosyć prosta: wybieramy dowolny kolor, malujemy nim dowolną jeszcze
niepomalowaną krawędź łączącą drużynę w środku z którąś z drużyn
w wierzchołkach
-kąta foremnego, a ostatnią w jego środku, tak jak na rysunku 1
(zamiast różnych kolorów są różne rodzaje linii). Teraz sprawa jest
dosyć prosta: wybieramy dowolny kolor, malujemy nim dowolną jeszcze
niepomalowaną krawędź łączącą drużynę w środku z którąś z drużyn
w wierzchołkach
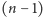 -kąta i następnie tym kolorem malujemy
wszystkie przekątne
-kąta i następnie tym kolorem malujemy
wszystkie przekątne
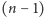 -kąta prostopadłe do danej krawędzi.
Na rysunku 2 widać dwa początkowe etapy kolorowania. Ponieważ
liczba
-kąta prostopadłe do danej krawędzi.
Na rysunku 2 widać dwa początkowe etapy kolorowania. Ponieważ
liczba
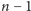 jest nieparzysta, to każda z wybranych krawędzi
łączących środek z wierzchołkiem
jest nieparzysta, to każda z wybranych krawędzi
łączących środek z wierzchołkiem
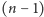 -kąta jest zawarta w jego
osi symetrii, a każda z
-kąta jest zawarta w jego
osi symetrii, a każda z
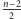 przekątnych łączących wierzchołek
z jego obrazem symetrycznym jest prostopadła do tej krawędzi (i nie jest
prostopadła do żadnej innej krawędzi łączącej środek z wierzchołkiem
przekątnych łączących wierzchołek
z jego obrazem symetrycznym jest prostopadła do tej krawędzi (i nie jest
prostopadła do żadnej innej krawędzi łączącej środek z wierzchołkiem
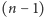 -kąta). W każdym kroku kolorujemy więc
-kąta). W każdym kroku kolorujemy więc
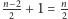 krawędzi naszego grafu.
krawędzi naszego grafu.
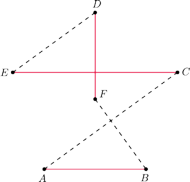
Rys. 2
Gdy byłem małym chłopcem, czyli we wczesnej podstawówce, bardzo interesowałem się piłką nożną i lubiłem tworzyć własne rozgrywki ligowe. Najpierw, oczywiście, trzeba było ułożyć terminarz spotkań. Liga polska liczyła wówczas 18 drużyn, a ja, rzecz jasna, nie znałem opisanego przed chwilą sposobu. A proste przepisanie terminarza ligi polskiej (i podmiana nazw drużyn) nie wchodziło w grę, bo w tamtych czasach zwyczajnie nie bardzo można było ten terminarz znaleźć (chyba że kolekcjonując gazety z całego sezonu – dziś wystarczyłoby kupić Skarb kibica, włączyć telegazetę lub wejść do Internetu). Nie byłem więc w stanie ułożyć terminarza dla ligi 18-drużynowej, ale za to wymyśliłem sprytny sposób na ułożenie terminarza dla ligi liczącej 16 drużyn (i tyle liczyły „moje” ligi).
Ułożyć terminarz dla ligi liczącej 4 drużyny jest łatwo – podzielmy więc naszą ligę na cztery grupy po cztery drużyny. Nazwijmy je A, B, C, D. Przez pierwsze trzy kolejki drużyny z poszczególnych grup grają między sobą. Co dalej? Teraz naszą ligę możemy potraktować po prostu jako ligę złożoną z czterech „drużyn” A, B, C, D. Mecz pomiędzy „drużynami” A i B trwa przez cztery kolejki i polega na tym, że każda drużyna z A gra z każdą z B (znowu jest to bardzo łatwe do zrealizowania). Zatem w kolejkach 4–7 mamy mecze A–B, C–D, w kolejkach 8–11 mecze A–C, B–D, a w 12–15 mecze A–D, B–C. I terminarz gotowy.
Na koniec powstaje pytanie: jeśli mamy ułożony terminarz, albo inaczej, kolorowanie grafu, to czy można tak rozmieścić jego wierzchołki, aby to kolorowanie było identyczne z opisaną wyżej konstrukcją? Innymi słowy, czy ten sposób układania jest jedyny z dokładnością do kolejności kolejek i układu drużyn? Może Czytelnik potrafi odpowiedzieć na to pytanie?