Kwadraty
Tym razem zajmiemy się trochę innymi kwadratami niż zazwyczaj. Chodzi
mianowicie o napisy postaci
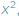 czyli sklejenie jakiegoś słowa (ciągu
liter)
czyli sklejenie jakiegoś słowa (ciągu
liter)
 z nim samym. Przykładowymi kwadratami występującymi
w języku polskim są słowa mama, kankan, rowerowe, wałowało, esemesem.
z nim samym. Przykładowymi kwadratami występującymi
w języku polskim są słowa mama, kankan, rowerowe, wałowało, esemesem.
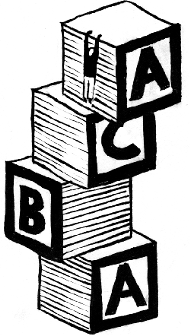
Jeśli rozważamy jakieś słowo, może nas interesować, czy jest ono kwadratem, ale także czy jakieś jego podsłowo (tzn. spójny fragment) jest kwadratem. Jeżeli nie, to słowo takie nazywamy bezkwadratowym. Zastanówmy się przez chwilę nad tym, jak konstruować słowa bezkwadratowe.
Najprościej wybrać słowo, w którym wszystkie litery są różne, np. abcde... Gdyby liter w alfabecie było nieskończenie wiele, to moglibyśmy w ten sposób skonstruować dowolnie długie słowo bezkwadratowe. Nie da się ukryć, że nie jest to zbyt ciekawy przykład. No to może spróbujmy wygenerować długie słowo bezkwadratowe nad jakimś mniejszym alfabetem?
Alfabet jednoliterowy na pewno nam nie pomoże. Załóżmy więc, że
mamy do dyspozycji dwie litery, a i b. Widać, że każde dwie kolejne
litery w słowie bezkwadratowym muszą być różne, a zatem nasze
słowo musi zaczynać się jakoś tak: aba... lub bab... Niestety, w obu tych
przykładach nie możemy dołożyć już żadnej litery, gdyż wówczas
otrzymamy kwadrat
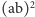 lub odpowiednio
lub odpowiednio
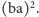 To oznacza, że
najdłuższe słowo bezkwadratowe nad alfabetem dwuliterowym ma tylko trzy
litery.
To oznacza, że
najdłuższe słowo bezkwadratowe nad alfabetem dwuliterowym ma tylko trzy
litery.
Kolejna próba: alfabet trzyliterowy. Znów konstruujemy słowo, biorąc zawsze
kolejną literę różną od poprzedniej. Daje to zawsze dwie możliwości
wyboru. W takim razie dodajmy warunek, że każda kolejna litera musi być
różna od środkowej litery dotychczasowego słowa – dokładniej, przy
wyznaczaniu
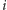 -tej litery interesuje nas litera o indeksie
-tej litery interesuje nas litera o indeksie
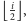 przy czym litery słowa numerujemy od zera. Jeżeli to kryterium wciąż
dopuszcza dwie możliwości, to wybieramy tę spośród niezabronionych liter,
która występuje wcześniej w alfabecie. W ten sposób otrzymujemy takie oto
słowo:
przy czym litery słowa numerujemy od zera. Jeżeli to kryterium wciąż
dopuszcza dwie możliwości, to wybieramy tę spośród niezabronionych liter,
która występuje wcześniej w alfabecie. W ten sposób otrzymujemy takie oto
słowo:

Okazuje się, że dowolnie długie słowo wygenerowane w ten sposób jest bezkwadratowe. Można ten fakt udowodnić formalnie, jednak w tym artykule zastosujemy podejście informatyczne natury eksperymentalnej: weźmiemy odpowiednio długie słowo tej postaci (np. złożone z miliona liter) i sprawdzimy za pomocą programu komputerowego, czy jest w tym słowie jakieś kwadratowe podsłowo. Jeśli okaże się, że nie, to zapewne wszystkie takie słowa są bezkwadratowe...
Nie jest wcale łatwo zaproponować efektywny, a zarazem nieskomplikowany
algorytm sprawdzający, czy dane słowo jest bezkwadratowe – zachęcamy
Czytelnika do próby samodzielnego zmierzenia się z tym problemem. Poniżej
przedstawiamy elegancki algorytm o złożoności czasowej
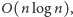 przy czym
przy czym
 to długość badanego słowa
to długość badanego słowa
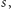 wzorowany na trudno
dostępnej i trochę zapomnianej pracy M. Maina i R. Lorentza sprzed
25 lat.
wzorowany na trudno
dostępnej i trochę zapomnianej pracy M. Maina i R. Lorentza sprzed
25 lat.
Zacznijmy od prostego sprawdzenia, czy w słowie
 znajduje się jakaś
para równych kolejnych liter – to eliminuje nam kwadraty słów długości 1.
W głównej części algorytmu wykonujemy
znajduje się jakaś
para równych kolejnych liter – to eliminuje nam kwadraty słów długości 1.
W głównej części algorytmu wykonujemy
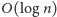 kroków;
w
kroków;
w
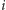 -tym kroku (dla
-tym kroku (dla
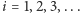 ) sprawdzamy, czy słowo
) sprawdzamy, czy słowo
 zawiera podsłowo kwadratowe
zawiera podsłowo kwadratowe
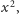 takie że długość
takie że długość
 (oznaczenie:
(oznaczenie:
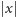 ) należy do przedziału domknięto-otwartego
) należy do przedziału domknięto-otwartego
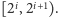 Wykonując taki krok, zakładamy, że
Wykonując taki krok, zakładamy, że
 nie zawiera
podsłów kwadratowych o długości połówki krótszej niż rozważane
w tym kroku. Naszym celem jest wykonanie każdego kroku w złożoności
czasowej
nie zawiera
podsłów kwadratowych o długości połówki krótszej niż rozważane
w tym kroku. Naszym celem jest wykonanie każdego kroku w złożoności
czasowej
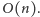
Poszukiwania żądanego kwadratu rozpoczynamy od podziału słowa
 na bloki długości
na bloki długości
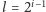 (jeżeli nie dzieli się równo, to końcowej,
krótszej grupy liter nie rozpatrujemy). Zauważmy, że jeżeli w
(jeżeli nie dzieli się równo, to końcowej,
krótszej grupy liter nie rozpatrujemy). Zauważmy, że jeżeli w
 występuje kwadrat
występuje kwadrat
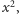 taki że
taki że
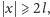 to pierwsze wystąpienie
to pierwsze wystąpienie
 w ramach
w ramach
 musi zawierać co najmniej jeden z bloków
podziału. Oznaczmy ten blok przez
musi zawierać co najmniej jeden z bloków
podziału. Oznaczmy ten blok przez
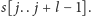 To samo podsłowo
pojawia się także na pozycji
To samo podsłowo
pojawia się także na pozycji
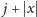 słowa
słowa
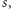 choć to drugie
wystąpienie nie musi już być blokiem podziału.
choć to drugie
wystąpienie nie musi już być blokiem podziału.
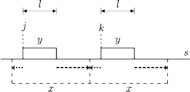
W naszym algorytmie rozważamy każdy kolejny blok
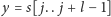 i poszukujemy wszystkich jego wystąpień w
i poszukujemy wszystkich jego wystąpień w
 zaczynających się na
pozycjach z przedziału
zaczynających się na
pozycjach z przedziału
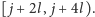 Co ciekawe, takie wystąpienia
mogą być co najwyżej dwa. Faktycznie, żadne dwa wystąpienia
Co ciekawe, takie wystąpienia
mogą być co najwyżej dwa. Faktycznie, żadne dwa wystąpienia
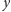 w ramach
w ramach
 nie mogą na siebie nachodzić ani nawet się stykać, gdyż
wówczas wyznaczałyby one kwadrat słowa o długości nie większej niż
nie mogą na siebie nachodzić ani nawet się stykać, gdyż
wówczas wyznaczałyby one kwadrat słowa o długości nie większej niż
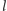 (dlaczego?). Stanowiłoby to sprzeczność z założeniem, że
(dlaczego?). Stanowiłoby to sprzeczność z założeniem, że
 nie zawiera kwadratu krótszego niż
nie zawiera kwadratu krótszego niż
Dla każdego wystąpienia
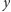 w
w
 na pozycji
na pozycji
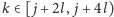 musimy jakoś sprawdzić, czy wystąpienia z pozycji
musimy jakoś sprawdzić, czy wystąpienia z pozycji
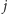 oraz
oraz
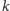 wyznaczają jakiś kwadrat
wyznaczają jakiś kwadrat
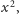 taki że
taki że
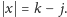 Poszukując
takiego kwadratu, wystarczy skupić się na badaniu równości par liter słowa
Poszukując
takiego kwadratu, wystarczy skupić się na badaniu równości par liter słowa
 o indeksach oddalonych o
o indeksach oddalonych o
 Najpierw sprawdzamy, czy
Najpierw sprawdzamy, czy
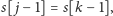
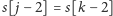 i tak dalej, aż natrafimy na
parę różnych liter albo aż dalszym indeksem dojdziemy do pozycji
i tak dalej, aż natrafimy na
parę różnych liter albo aż dalszym indeksem dojdziemy do pozycji
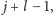 co oznacza, że znaleźliśmy kwadrat. Następnie powtarzamy to
postępowanie, ale tym razem idąc do przodu, tzn. sprawdzamy, jak długo
zachodzi
co oznacza, że znaleźliśmy kwadrat. Następnie powtarzamy to
postępowanie, ale tym razem idąc do przodu, tzn. sprawdzamy, jak długo
zachodzi
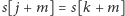 dla
dla
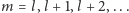 Tym razem
możemy zatrzymać się, jeśli liczba wykonanych tutaj kroków powiększona
o liczbę kroków wykonanych wcześniej jest nie mniejsza niż
Tym razem
możemy zatrzymać się, jeśli liczba wykonanych tutaj kroków powiększona
o liczbę kroków wykonanych wcześniej jest nie mniejsza niż
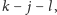 patrz rysunek. Jeżeli nie dojdziemy do wartości
patrz rysunek. Jeżeli nie dojdziemy do wartości
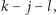 to łatwo
zauważyć, że rozważana para wystąpień podsłowa
to łatwo
zauważyć, że rozważana para wystąpień podsłowa
 nie wyznacza
kwadratu.
nie wyznacza
kwadratu.
Na tym rozumowaniu oparty jest poniższy pseudokod algorytmu wykrywania
kwadratu w słowie
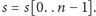
for
 to
to
 do
do if
 then return true;
then return true; 
while
 do
do 
while
 do
do  wystąpienia
wystąpienia
 zaczynające
się
zaczynające
się na pozycjach z przedziału [j + 2l, j + 4l);
for each
 do
do lewo := długość najdłuższego wspólnego sufiksu słów
 i
i

prawo := długość najdłuższego wspólnego prefiksu
słów
 i
i

if lewo + prawo
 then return true;
then return true; 

return false;
end function
Zastanówmy się nad złożonością czasową tego algorytmu, przy okazji
uzupełniając szczegóły techniczne jego implementacji. Pierwszym interesującym
miejscem jest wyznaczanie zbioru
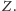 Znane są różne efektywne
algorytmy wyszukiwania wzorca (u nas jest to słowo
Znane są różne efektywne
algorytmy wyszukiwania wzorca (u nas jest to słowo
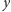 ) w tekście
(u nas: zadany fragment słowa
) w tekście
(u nas: zadany fragment słowa
 ), np. algorytmy Knutha–Morrisa–Pratta,
Boyera–Moore’a itp. W tym miejscu czeka nas jednak kolejne zaskoczenie:
otóż w naszym programie w ogóle nie musimy używać żadnego
z tych wysublimowanych algorytmów! Zaczynamy od sprawdzenia,
literka po literce, czy
), np. algorytmy Knutha–Morrisa–Pratta,
Boyera–Moore’a itp. W tym miejscu czeka nas jednak kolejne zaskoczenie:
otóż w naszym programie w ogóle nie musimy używać żadnego
z tych wysublimowanych algorytmów! Zaczynamy od sprawdzenia,
literka po literce, czy
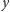 pasuje do
pasuje do
 od pozycji
od pozycji
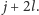 Jak w pewnym momencie zakończymy to sprawdzanie (albo znajdując
wystąpienie
Jak w pewnym momencie zakończymy to sprawdzanie (albo znajdując
wystąpienie
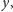 albo wskutek natrafienia na parę różnych liter na
odpowiadających pozycjach), to kolejną próbę przypasowania słowa
albo wskutek natrafienia na parę różnych liter na
odpowiadających pozycjach), to kolejną próbę przypasowania słowa
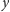 wykonujemy od pierwszej pozycji w
wykonujemy od pierwszej pozycji w
 następującej za
wszystkimi przejrzanymi. Faktycznie, wystąpienie słowa
następującej za
wszystkimi przejrzanymi. Faktycznie, wystąpienie słowa
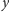 w
w
 nie może nachodzić na żadne inne wystąpienie niepustego prefiksu
słowa
nie może nachodzić na żadne inne wystąpienie niepustego prefiksu
słowa
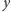 w
w
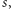 gdyż wówczas
gdyż wówczas
 zawierałoby kwadrat
jakiegoś prefiksu słowa
zawierałoby kwadrat
jakiegoś prefiksu słowa
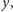 a przecież
a przecież
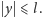 W ten sposób
znajdujemy szukane co najwyżej dwa elementy zbioru
W ten sposób
znajdujemy szukane co najwyżej dwa elementy zbioru
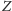 w czasie
w czasie
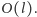
Kolejny ciekawy moment to wyznaczanie wartości lewo i prawo,
wykonywane troszkę inaczej niż w opisie słownym algorytmu. Uzasadnienie
poprawności pomijamy, przyjrzyjmy się kwestii złożoności czasowej. Łączna
liczba operacji wykonywanych tutaj może być całkiem duża. Zauważmy
jednak, że jeśli przy wyznaczaniu wspólnego sufiksu i prefiksu wykonamy
więcej niż
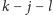 operacji, to na pewno zaraz potem zakończymy
działanie algorytmu, więc możemy sobie ten jeden raz pozwolić na
wykonanie nawet i rzędu
operacji, to na pewno zaraz potem zakończymy
działanie algorytmu, więc możemy sobie ten jeden raz pozwolić na
wykonanie nawet i rzędu
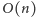 operacji. W przeciwnym razie
liczba tych operacji nie przekroczy
operacji. W przeciwnym razie
liczba tych operacji nie przekroczy
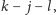 która to wartość
– przypomnijmy – jest nie większa niż
która to wartość
– przypomnijmy – jest nie większa niż
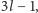 czyli jest rzędu
czyli jest rzędu
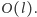
Widzimy zatem, że wnętrze wewnętrznej pętli while wykonujemy
– poza ewentualnie jedynym jej obrotem, kończącym cały algorytm
– w czasie
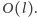 Pętla ta wykonuje
Pętla ta wykonuje
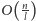 obrotów, co
pokazuje, że koszt czasowy jednego obrotu zewnętrznej pętli while to
obrotów, co
pokazuje, że koszt czasowy jednego obrotu zewnętrznej pętli while to
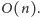 Ta, z kolei, wykonuje co najwyżej
Ta, z kolei, wykonuje co najwyżej
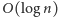 obrotów, skąd
wnosimy, że rzeczywiście opisany algorytm ma złożoność czasową
obrotów, skąd
wnosimy, że rzeczywiście opisany algorytm ma złożoność czasową
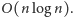
Na koniec pytanie do Czytelnika: czy można ten algorytm jakoś łatwo przerobić, tak aby wykrywał wszystkie kwadraty w słowie?