Równania napisów
Przyjrzyjmy się problemowi równań napisów: dla ustalonego alfabetu, np. 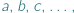 piszemy równania używające liter z tegoż alfabetu oraz zmiennych, które będziemy oznaczać przez
piszemy równania używające liter z tegoż alfabetu oraz zmiennych, które będziemy oznaczać przez 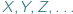 Dla uproszczenia pomyślmy o jednym równaniu, np.
Dla uproszczenia pomyślmy o jednym równaniu, np. 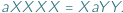 Rozwiązaniem będą takie napisy, złożone z liter alfabetu, że po podstawieniu pod zmienne uzyskamy takie same napisy....
Rozwiązaniem będą takie napisy, złożone z liter alfabetu, że po podstawieniu pod zmienne uzyskamy takie same napisy....
W naszym przykładzie podstawienie 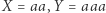 jest rozwiązaniem. Innym przykładem jest równanie
jest rozwiązaniem. Innym przykładem jest równanie 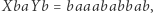 którego rozwiązaniem jest np.
którego rozwiązaniem jest np. 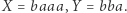 Równania tego typu rozważane były od lat 60. XX wieku, z jednej strony ze względu na związki z 10. problemem Hilberta, z drugiej ze względu na związki z teorią grup… Ale obie te historie to tematy na osobne artykuły.
Równania tego typu rozważane były od lat 60. XX wieku, z jednej strony ze względu na związki z 10. problemem Hilberta, z drugiej ze względu na związki z teorią grup… Ale obie te historie to tematy na osobne artykuły.
Pierwszy sposób rozwiązywania tego typu równań podał G. Makanin w 1977 roku, w roku 1999 inne, dużo prostsze podejście zaproponował W. Plandowski. My przyjrzymy się dziś rozwiązaniu upraszczającemu drugie z nich, na podstawie mojego artykułu Recompression: A Simple and Powerful Technique for Word Equations, (Journal of the ACM, 2016 63:1, art. 4).
Zanim przystąpimy do prezentacji sposobu rozwiązywania takich równań, należałoby ustalić, do czego będziemy dążyć: chcemy podać algorytm, czyli systematyczny przepis pokazujący, jak uzyskać rozwiązanie (lub stwierdzić, że go nie ma). Przykładem algorytmu dla układu równań liniowych jest: "Powtarzaj: weź pierwsze równanie, jeśli jest niesprzeczne i zawiera zmienną, to wylicz jedną zmienną w oparciu o inne i podstaw do pozostałych równań, usuń równanie". Przykładem algorytmu dla równania kwadratowego 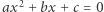 jest: "Wylicz
jest: "Wylicz 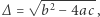 jeśli
jeśli 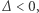 to nie ma rozwiązań, w przeciwnym przypadku rozwiązania to
to nie ma rozwiązań, w przeciwnym przypadku rozwiązania to 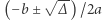 ". Podamy tego typu algorytm, choć dłuższy i bardziej skomplikowany, dla równań napisów.
". Podamy tego typu algorytm, choć dłuższy i bardziej skomplikowany, dla równań napisów.
Nasz algorytm będzie wielokrotnie sprawdzał niezależnie kilka możliwości, np. osobno sprawdzi możliwości, że pierwsza litera podstawienia pod  to
to  lub
lub 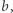 a potem osobno, czy poza tą jedną literą coś jeszcze w podstawieniu jest, czy nie, itd. Jeśli istnieje rozwiązanie, to algorytm znajdzie je dla którejś sekwencji możliwości, dla innych być może nie znajdzie. Nie brzmi to jak dobry pomysł - w takim razie algorytm mógłby po prostu przejrzeć wszystkie możliwe podstawienia, litera po literze… Dlatego też zagwarantujemy coś jeszcze - algorytm będzie przekształcał równanie w taki sposób, że dla którejś z możliwości wiodących do rozwiązania rozważane równanie zawsze będzie miało najwyżej
a potem osobno, czy poza tą jedną literą coś jeszcze w podstawieniu jest, czy nie, itd. Jeśli istnieje rozwiązanie, to algorytm znajdzie je dla którejś sekwencji możliwości, dla innych być może nie znajdzie. Nie brzmi to jak dobry pomysł - w takim razie algorytm mógłby po prostu przejrzeć wszystkie możliwe podstawienia, litera po literze… Dlatego też zagwarantujemy coś jeszcze - algorytm będzie przekształcał równanie w taki sposób, że dla którejś z możliwości wiodących do rozwiązania rozważane równanie zawsze będzie miało najwyżej 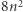 liter i
liter i 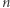 zmiennych, gdzie
zmiennych, gdzie  to długość równania wejściowego. W szczególności dla niektórych możliwości nie znajdziemy rozwiązania (trudno!), a inne doprowadzą nas do równania dłuższego niż
to długość równania wejściowego. W szczególności dla niektórych możliwości nie znajdziemy rozwiązania (trudno!), a inne doprowadzą nas do równania dłuższego niż 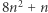 - wtedy algorytm przestaje dalej liczyć. Takie podejście można też zrealizować inaczej, bez odwoływania się do sprawdzania wszystkich możliwości: możemy wypisać wszystkie równania długości najwyżej
- wtedy algorytm przestaje dalej liczyć. Takie podejście można też zrealizować inaczej, bez odwoływania się do sprawdzania wszystkich możliwości: możemy wypisać wszystkie równania długości najwyżej 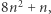 zaznaczyć, które równania możemy przekształcić w które, i sprawdzić, czy potrafimy przekształcić wejściowe równanie w jakieś bardzo proste niesprzeczne równanie, np.
zaznaczyć, które równania możemy przekształcić w które, i sprawdzić, czy potrafimy przekształcić wejściowe równanie w jakieś bardzo proste niesprzeczne równanie, np. 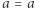 albo
albo 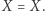
Od teraz skupimy się na wykazaniu, że algorytm zawsze ma "dobry wybór", tj. potrafi przekształcić niesprzeczne równanie długości nie większej niż 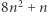 w niesprzeczne równanie długości również nie większej niż
w niesprzeczne równanie długości również nie większej niż 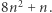 Ważne jest też, że niezależnie od wyboru nie przekształcimy równania sprzecznego w niesprzeczne.
Ważne jest też, że niezależnie od wyboru nie przekształcimy równania sprzecznego w niesprzeczne.
Równanie napisów może mieć wiele rozwiązań i algorytm jest w stanie podać reprezentację wszystkich; dla uproszczenia będziemy wymagać jedynie, o ile istnieje, aby podał dowolne. W szczególności: jeśli istnieje rozwiązanie, to istnieje też takie, które używa tylko liter występujących w równaniu, choć sam alfabet może być większy - wszystkie inne litery w rozwiązaniu można zastąpić przez ustaloną literę; nowe podstawienie dalej jest rozwiązaniem. Będziemy też zakładać, że podstawienie pod zmienną jest niepuste, tj. w podstawieniu 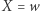 słowo
słowo 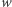 ma dodatnią długość.
ma dodatnią długość.
Aby rozwiązać równanie napisów, będziemy skracać jego krótkie fragmenty: popatrzmy jeszcze raz na równanie 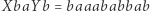 (które ma rozwiązanie
(które ma rozwiązanie 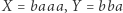 ): jeśli zastąpimy
): jeśli zastąpimy 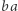 przez "świeżą", tj. nieużywaną w równaniu, literę
przez "świeżą", tj. nieużywaną w równaniu, literę 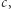 to otrzymane równanie
to otrzymane równanie 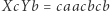 ma rozwiązanie
ma rozwiązanie 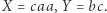 Łatwo też sprawdzić, że jeśli nowe równanie ma rozwiązanie, to stare też ma - wystarczy zamienić w podstawieniu każde
Łatwo też sprawdzić, że jeśli nowe równanie ma rozwiązanie, to stare też ma - wystarczy zamienić w podstawieniu każde  przez
przez 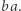 Niestety, ten pomysł nie działa, jeśli w oryginalnym równaniu spróbujemy zastąpić
Niestety, ten pomysł nie działa, jeśli w oryginalnym równaniu spróbujemy zastąpić 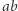 przez
przez 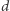 : po lewej stronie równania nie ma żadnego
: po lewej stronie równania nie ma żadnego 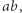 w podstawieniu
w podstawieniu 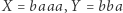 również nie ma, jest za to po prawej stronie równania. Problemem jest to, że
również nie ma, jest za to po prawej stronie równania. Problemem jest to, że 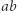 jest częściowo w podstawieniu i częściowo poza. Parę
jest częściowo w podstawieniu i częściowo poza. Parę 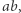 gdzie
gdzie 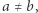 nazwiemy złą (dla ustalonego rozwiązania), jeśli
nazwiemy złą (dla ustalonego rozwiązania), jeśli 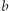 jest pierwszą literą podstawienia pod
jest pierwszą literą podstawienia pod 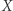 oraz
oraz 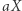 występuje w równaniu lub
występuje w równaniu lub  jest ostatnią literą podstawienia pod
jest ostatnią literą podstawienia pod 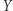 oraz
oraz 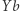 występuje w równaniu (lub dla powyższych założeń
występuje w równaniu (lub dla powyższych założeń 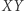 występuje w równaniu). Parę, która nie jest zła, nazwiemy dobrą. Jeśli para
występuje w równaniu). Parę, która nie jest zła, nazwiemy dobrą. Jeśli para 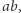 gdzie
gdzie 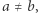 jest dobra, to skrócenie
jest dobra, to skrócenie 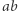 daje równanie, które ma odpowiadające, krótsze rozwiązanie. Jednocześnie, jeśli nowe równanie ma rozwiązanie, to stare też miało: wystarczy każde
daje równanie, które ma odpowiadające, krótsze rozwiązanie. Jednocześnie, jeśli nowe równanie ma rozwiązanie, to stare też miało: wystarczy każde  zastąpić przez
zastąpić przez 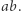
Co do złych par, to łatwo zauważyć, że jeśli równanie ma  wystąpień zmiennych, to jest najwyżej
wystąpień zmiennych, to jest najwyżej 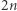 różnych złych par: po jednej na każdą stronę zmiennej. Co więcej, ustaloną złą parę łatwo udobruchać (czyli uczynić dobrą): jeśli
różnych złych par: po jednej na każdą stronę zmiennej. Co więcej, ustaloną złą parę łatwo udobruchać (czyli uczynić dobrą): jeśli 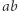 jest zła, to dla każdej zmiennej sprawdzamy: jeśli jej podstawienie zaczyna się na
jest zła, to dla każdej zmiennej sprawdzamy: jeśli jej podstawienie zaczyna się na 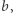 czyli
czyli 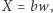 to zastępujemy
to zastępujemy 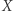 przez
przez 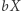 (a podstawienie przez
(a podstawienie przez 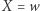 ), analogicznie, jeśli podstawienie kończy się na
), analogicznie, jeśli podstawienie kończy się na 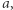 to zastępujemy
to zastępujemy 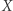 przez
przez 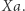 Jeśli w ten sposób podstawienie za
Jeśli w ten sposób podstawienie za 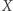 stało się puste, to usuwamy
stało się puste, to usuwamy 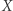 z równania. Łatwo sprawdzić, że nowe równanie ma rozwiązanie oraz para
z równania. Łatwo sprawdzić, że nowe równanie ma rozwiązanie oraz para 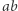 jest dobra; jeśli zaś nowe równanie ma rozwiązanie, to miało je też stare równanie: wystarczy dokleić litery, które "wypchnęliśmy" ze zmiennych. W nowym równaniu możemy skrócić
jest dobra; jeśli zaś nowe równanie ma rozwiązanie, to miało je też stare równanie: wystarczy dokleić litery, które "wypchnęliśmy" ze zmiennych. W nowym równaniu możemy skrócić 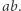
Złe pary to nie jedyny problem: skoro zakładamy, że w parze 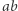 litery
litery 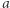 i
i 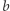 są różne, to nie potrafimy skrócić długich powtórzeń jednej litery, np. nie wiemy, co zrobić z równaniem
są różne, to nie potrafimy skrócić długich powtórzeń jednej litery, np. nie wiemy, co zrobić z równaniem 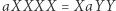 z pierwszego przykładu. Zamiast skracać pary, będziemy skracać maksymalne powtórzenia:
z pierwszego przykładu. Zamiast skracać pary, będziemy skracać maksymalne powtórzenia: 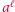 jest maksymalnym powtórzeniem
jest maksymalnym powtórzeniem 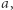 jeśli na lewo i prawo nie ma litery
jeśli na lewo i prawo nie ma litery 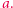 Podobnie jak w przypadku par, możemy zdefiniować, co to znaczy, że litera
Podobnie jak w przypadku par, możemy zdefiniować, co to znaczy, że litera 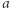 jest zła (jest zmienna
jest zła (jest zmienna 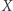 zaczynająca się na
zaczynająca się na  i
i 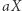 występuje w równaniu lub…) i dobra. Jeśli
występuje w równaniu lub…) i dobra. Jeśli  jest dobre, to możemy równocześnie zastąpić wszystkie maksymalne wystąpienia
jest dobre, to możemy równocześnie zastąpić wszystkie maksymalne wystąpienia 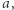 powiedzmy dla każdego
powiedzmy dla każdego 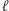 zastępujemy maksymalne
zastępujemy maksymalne 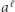 przez
przez 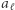 ; przy czym
; przy czym 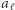 to tylko wygodna nazwa dla nas, algorytm nie musi potem pamiętać, że ta litera powstała z
to tylko wygodna nazwa dla nas, algorytm nie musi potem pamiętać, że ta litera powstała z 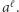 Jeśli
Jeśli 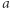 jest zła, to chcemy ją "udobruchać", ale zastąpienie
jest zła, to chcemy ją "udobruchać", ale zastąpienie 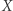 przez
przez 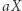 może nie wystarczyć, gdyż podstawienie pod
może nie wystarczyć, gdyż podstawienie pod 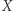 może dalej zaczynać się na
może dalej zaczynać się na 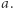 Zamiast tego, jeśli
Zamiast tego, jeśli 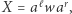 gdzie
gdzie 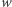 nie zaczyna się ani nie kończy na
nie zaczyna się ani nie kończy na 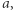 to zastępujemy
to zastępujemy 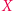 przez
przez 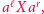 odpowiednio zmieniając podstawienie pod
odpowiednio zmieniając podstawienie pod 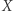 (teraz
(teraz 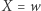 ). Wszystkie możliwe
). Wszystkie możliwe 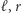 chcemy sprawdzić osobno i tu pojawia się problem:
chcemy sprawdzić osobno i tu pojawia się problem: 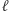 i
i  mogą być dowolnie duże. Wiadomo jednak, że jeśli istnieje rozwiązanie równania, to istnieje też rozwiązanie, w którym wszystkie takie
mogą być dowolnie duże. Wiadomo jednak, że jeśli istnieje rozwiązanie równania, to istnieje też rozwiązanie, w którym wszystkie takie 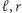 mają najwyżej wykładniczą długość. To wciąż dużo, ale zamiast pisać
mają najwyżej wykładniczą długość. To wciąż dużo, ale zamiast pisać 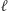 razy
razy 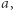 możemy zapisać
możemy zapisać 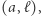 a zapis pozycyjny
a zapis pozycyjny 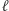 ma wielomianowo wiele cyfr. I tak zaraz skrócimy wszystkie maksymalne powtórzenia
ma wielomianowo wiele cyfr. I tak zaraz skrócimy wszystkie maksymalne powtórzenia 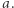 Tak samo jak dla par możemy wykazać, że jest najwyżej
Tak samo jak dla par możemy wykazać, że jest najwyżej 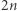 złych liter, a jeśli rozpatrzymy jednocześnie złe pary i litery, to podobnie stwierdzamy, że w sumie złych par i liter jest najwyżej
złych liter, a jeśli rozpatrzymy jednocześnie złe pary i litery, to podobnie stwierdzamy, że w sumie złych par i liter jest najwyżej 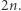
Teraz możemy już podać wybory algorytmu, które prowadzą do rozwiązania, a równanie ma niezmiennie co najwyżej 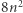 liter (i najwyżej
liter (i najwyżej 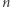 zmiennych): dla danego równania, jeśli istnieje dobra para lub litera, to skracamy ją. Jeśli są tylko złe pary i litery, to wybieramy taką, że po jej udobruchaniu oraz skróceniu otrzymane równanie jest najkrótsze.
zmiennych): dla danego równania, jeśli istnieje dobra para lub litera, to skracamy ją. Jeśli są tylko złe pary i litery, to wybieramy taką, że po jej udobruchaniu oraz skróceniu otrzymane równanie jest najkrótsze.
Przeanalizujmy algorytm dla tych możliwości: zauważmy najpierw, że jeśli równanie nie ma rozwiązania, to nieważne, co zrobimy, nowe równanie również nie będzie miało rozwiązania. Twierdzimy też, że przy właściwych wyborach równanie nigdy nie będzie miało więcej niż 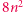 liter, gdzie
liter, gdzie 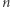 to długość równania danego na wejściu: Jeśli istnieje dobra para lub litera, to po jej skróceniu nowe równanie jest krótsze niż stare. A co, jeśli są tylko złe pary i litery? Niech równanie ma
to długość równania danego na wejściu: Jeśli istnieje dobra para lub litera, to po jej skróceniu nowe równanie jest krótsze niż stare. A co, jeśli są tylko złe pary i litery? Niech równanie ma 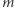 liter, nie licząc zmiennych. Różnych złych par i liter jest w sumie najwyżej
liter, nie licząc zmiennych. Różnych złych par i liter jest w sumie najwyżej 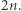 Dla każdej litery rozpatrzmy literę na prawo (lub lewo, dla ostatniej); ta sąsiednia litera może pochodzić z podstawienia pod zmienną. Razem tworzą parę albo są częścią maksymalnego bloku. Czyli dla każdego wystąpienia litery
Dla każdej litery rozpatrzmy literę na prawo (lub lewo, dla ostatniej); ta sąsiednia litera może pochodzić z podstawienia pod zmienną. Razem tworzą parę albo są częścią maksymalnego bloku. Czyli dla każdego wystąpienia litery 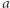 w równaniu istnieje zła para lub litera, której wystąpienie zawiera to ustalone wystąpienie
w równaniu istnieje zła para lub litera, której wystąpienie zawiera to ustalone wystąpienie 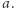 Skrócenie tej pary/litery usunie to ustalone wystąpienie
Skrócenie tej pary/litery usunie to ustalone wystąpienie 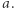 Jako że jest
Jako że jest 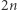 złych par i liter, "średnio" skrócenie usunie przynajmniej
złych par i liter, "średnio" skrócenie usunie przynajmniej 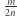 liter oraz wprowadzi co najwyżej połowę z tej liczby (skrócenie pary usuwa dwie litery i dodaje jedną, a skrócenie bloku liter usuwa wiele liter i dodaje jedną). Tak więc istnieje takie skrócenie, które w sumie skróci równanie o przynajmniej
liter oraz wprowadzi co najwyżej połowę z tej liczby (skrócenie pary usuwa dwie litery i dodaje jedną, a skrócenie bloku liter usuwa wiele liter i dodaje jedną). Tak więc istnieje takie skrócenie, które w sumie skróci równanie o przynajmniej 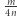 liter. Musimy też wykonać jedno udobruchanie, które wprowadza do równania najwyżej
liter. Musimy też wykonać jedno udobruchanie, które wprowadza do równania najwyżej 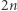 liter: udobruchanie litery wprowadza długie powtórzenia tej litery, ale zaraz każde takie powtórzenie zostanie zastąpione przez jedną literę. Tak więc nowe równanie ma najwyżej
liter: udobruchanie litery wprowadza długie powtórzenia tej litery, ale zaraz każde takie powtórzenie zostanie zastąpione przez jedną literę. Tak więc nowe równanie ma najwyżej 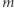 (stare litery)
(stare litery) 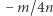 (usunięte przez skrócenie)
(usunięte przez skrócenie) 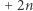 (udobruchanie) liter. Oszacujmy:
(udobruchanie) liter. Oszacujmy:
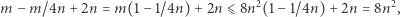 |
jedyna nierówność wynika z ograniczenia 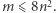 I to jest koniec: dla podanych wyżej wyborów równanie znajdzie rozwiązanie i równania, które rozważa, mają najwyżej
I to jest koniec: dla podanych wyżej wyborów równanie znajdzie rozwiązanie i równania, które rozważa, mają najwyżej 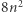 liter (i najwyżej
liter (i najwyżej 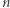 zmiennych).
zmiennych).
A czego nie wiemy o równaniach napisów? Dokładniejsza analiza algorytmu pokazuje, że jeśli istnieje rozwiązanie, to istnieje też rozwiązanie podwójnie wykładnicze. Nie jest jednak znane równanie, którego najkrótsze rozwiązanie jest ponad wykładnicze; popularna jest hipoteza, że jeśli istnieje rozwiązanie, to istnieje też rozwiązanie wykładnicze. Do równań napisów można też dodać dodatkowe warunki na rozwiązanie, np. żądać, by suma długości podstawień pod 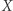 i
i 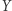 była równa długości podstawienia pod
była równa długości podstawienia pod 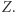 Nie wiadomo, czy równania napisów z liniowymi warunkami na długości podstawień można rozwiązać.
Nie wiadomo, czy równania napisów z liniowymi warunkami na długości podstawień można rozwiązać.
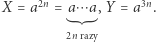
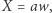 to sprawdzając możliwość, że pierwsza litera to
to sprawdzając możliwość, że pierwsza litera to 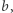 nie znajdziemy rozwiązania.
nie znajdziemy rozwiązania.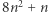 ręcznie nie jest możliwe, ale dla komputera nie jest to problem, o ile
ręcznie nie jest możliwe, ale dla komputera nie jest to problem, o ile 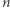 nie jest za duże.
nie jest za duże.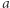 ". Sprowadzamy problem do równania liniowego, w którym niewiadomymi są długości napisów podstawień. To też nie jest zupełnie prosty problem, ale istnieją znane od dawna algorytmy, co znów jest tematem na osobny artykuł...
". Sprowadzamy problem do równania liniowego, w którym niewiadomymi są długości napisów podstawień. To też nie jest zupełnie prosty problem, ale istnieją znane od dawna algorytmy, co znów jest tematem na osobny artykuł...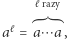 czyli
czyli  razy powtórzone
razy powtórzone 
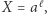 to zastępujemy
to zastępujemy 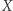 przez
przez 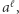 usuwając przy okazji
usuwając przy okazji 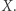
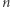 zmiennych.
zmiennych.