Pół szklanki mocnego kodu
Alchemia
Witajcie, Młodzi Alchemicy! Na dzisiejszym spotkaniu nie będziemy się zajmować tak przebrzmiałym tematem, jak zamiana zwykłego metalu w złoto... (Kto jeszcze nie wie, jak to należy prawidłowo robić, może przeczytać przepis na marginesie niniejszych notatek.) Przed nami znacznie ciekawszy problem: Jak z maliny wydobyć wolfram?
Okazuje się to całkiem proste, pod warunkiem, że wydobędziemy nie "zwykły" wolfram, tylko Wolfram Language. A i malina nie będzie zwykła: to popularny komputerek wielkości karty kredytowej, o apetycznej nazwie Raspberry Pi.

Raspberry Pi 3
W rzeczywistości osiągniemy jeszcze więcej: mając ten komputerek, będziemy mogli uruchomić na nim pełną (no, prawie pełną) wersję najnowszej Mathematiki, potężnego systemu obliczeń symbolicznych. Na pozór nie wydaje się to szczególnym osiągnięciem, gdyż każdy może to samo zrobić na dowolnym laptopie - pod warunkiem wszakże, że wcześniej wyasygnuje pokaźną sumkę na zakup licencji (uczciwie dodajmy, że jeśli jest uczniem lub studentem, wystarczy skromne 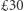 za półroczne użytkowanie). Jednak na Raspberry Pi możemy mieć ten software natychmiast, legalnie (do użytku niekomercyjnego) i... całkowicie za darmo!
za półroczne użytkowanie). Jednak na Raspberry Pi możemy mieć ten software natychmiast, legalnie (do użytku niekomercyjnego) i... całkowicie za darmo!
Oczywiście, jest pewien haczyk: możliwości nawet najmocniejszego Raspberry Pi są daleko poniżej laptopa ze średniej półki, więc zestaw zadań, jakie można wygodnie rozwiązywać w Mathematice na Raspberry Pi jest tym samym mocno ograniczony. Z drugiej strony, ten mały komputerek pozwala na prosty i tani kontakt ze światem realnym (przez możliwość podłączenia rozmaitych czujników: światła, temperatury itp., a także mikrofonu i kamery). Co więcej, jego Mathematica - dokładniej Wolfram Language, w którym ją programujemy - ma rozszerzenia pozwalające w prosty sposób to wykorzystać. No i - last but not least - zabawa z Malinką jest przednia (moim zdaniem, dla początkujących lepsza niż z Arduino), działa też na nim programowalny w paru językach, w tym: Pythonie i Mathematice... Minecraft! (W wersji pocket edition.)
Zaczynamy od instalacji systemu operacyjnego Raspbian (specjalna wersja Linuxa) na karcie microSD - która zastępuje dysk w Raspberry Pi - a potem całość uruchamiamy i aktualizujemy. Oprogramowanie Wolframa już tam będzie.
Mając w jednej garści i Malinkę, i Wolframa, aż korci, aby dokładając stosowne czujniki, szybko transmutować tę parę - np. w parapetową stację pogodową. Dziś jednak skupimy się tylko na zabawie z samym Wolframem (czyli Mathematiką) i dokonamy "alchemicznego" przekształcenia garści liczb w obiekty o naturalnym kształcie, takim jak kwiaty, nasiona, rozgwiazdy.

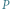 ma współrzędne biegunowe
ma współrzędne biegunowe 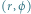
Wybierzemy sześć liczb: 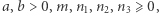 a następnie zdefiniujemy na płaszczyźnie krzywą we współrzędnych biegunowych
a następnie zdefiniujemy na płaszczyźnie krzywą we współrzędnych biegunowych 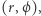 zadając promień wodzący wzorem
zadając promień wodzący wzorem
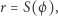
gdzie
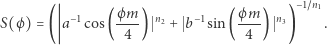
Powyższy wzór podał w 1999 roku belgijski botanik Johan Gielis i - zachwycony tym, jak różnorodne kształty można z niego uzyskać - ochrzcił bez zbędnej skromności superformułą. A następnie, w co trudno uwierzyć, swój pomysł... opatentował, zob. patents.google.com/patent/EP1177529B1. My jednak zauważmy (Gielis oczywiście też to wiedział), że jest to uogólnienie wzoru na elipsę poprzez umożliwienie wyboru potęg: faktycznie, dla 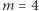 i
i 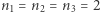 dostajemy zwyczajne równanie elipsy. Gielis poszedł jeszcze dalej i w swój wzór radośnie wplótł możliwość dalszego skalowania promienia:
dostajemy zwyczajne równanie elipsy. Gielis poszedł jeszcze dalej i w swój wzór radośnie wplótł możliwość dalszego skalowania promienia:
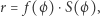
gdzie 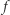 jest, hmm…, dowolną funkcją...
jest, hmm…, dowolną funkcją...

Czy potrafisz znaleźć parametry funkcji 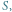 które generują kształty podobne do tych na ikonie Mathematiki powyżej?
które generują kształty podobne do tych na ikonie Mathematiki powyżej?
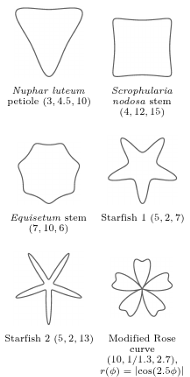
Jednak nawet gdy 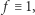 efekty wyboru 6 parametrów potrafią być intrygujące, co nie powinno nas dziwić: po prostu mamy całkiem dużo stopni swobody. Jak trzeźwo zauważył Eric Weisstein, redaktor strony mathworld.wolfram.com/Superellipse.html, już John von Neumann miał sarkastycznie (choć może z pewną przesadą) powiedzieć:
efekty wyboru 6 parametrów potrafią być intrygujące, co nie powinno nas dziwić: po prostu mamy całkiem dużo stopni swobody. Jak trzeźwo zauważył Eric Weisstein, redaktor strony mathworld.wolfram.com/Superellipse.html, już John von Neumann miał sarkastycznie (choć może z pewną przesadą) powiedzieć:
Przy czterech parametrach [krzywej] dopasuję ją do [kształtu] słonia; przy pięciu, będzie machał trąbą.
No to do roboty! Wykorzystajmy Mathematikę do rysowania krzywych zadanych superformułą. Dzięki możliwości wygodnego definiowania wykresów zależnych od parametrów, a także umiejętności rysowania krzywych zadanych wprost we współrzędnych biegunowych, całość zamkniemy w dwu liniach kodu, na który głównie składa się seria zagnieżdżonych wywołań funkcji:

Należy pamiętać o dziwnym zwyczaju zatwierdzania każdej instrukcji nie przez zwykły Enter, tylko przez kombinację klawiszy Shift+Enter.
Ten krótki kod daje nam przedsmak charakteru języka Mathematiki, czyli Wolfram Language. Kilka rzeczy, które od razu rzucają się w oczy, to:
- argumenty funkcji otacza się nawiasami kwadratowymi,
- nazwy funkcji wbudowanych (np. sinus) pisze się wielką literą.
W pierwszej linii programu definiujemy funkcję 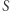 (dla uproszczenia, zmienną
(dla uproszczenia, zmienną 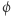 w kodzie zamieniamy na
w kodzie zamieniamy na 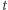 ; ponieważ parametry
; ponieważ parametry 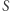 też traktujemy jako następne jej argumenty, w kodzie powyżej definiujemy w efekcie funkcję siedmiu argumentów). Definiując w Mathematice własną funkcję, korzystamy z operatora ":=", a argumenty po lewej stronie definicji funkcji musimy - co użytkownikom innych języków może wydawać się dziwaczne - wyróżniać przyrostkiem "_". Dlatego funkcję, która wyznacza oba pierwiastki zadanego trójmianu kwadratowego
też traktujemy jako następne jej argumenty, w kodzie powyżej definiujemy w efekcie funkcję siedmiu argumentów). Definiując w Mathematice własną funkcję, korzystamy z operatora ":=", a argumenty po lewej stronie definicji funkcji musimy - co użytkownikom innych języków może wydawać się dziwaczne - wyróżniać przyrostkiem "_". Dlatego funkcję, która wyznacza oba pierwiastki zadanego trójmianu kwadratowego 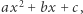 zapisalibyśmy Pierwiastki[a_, b_, c_]:= Roots[a*x^2+b*x+c==0, x] (wbudowana funkcja Roots rozwiązuje równania wielomianowe), a następnie użyli na przykład tak: Pierwiastki[2,0, -m]. W linii numer 3 najważniejsza jest funkcja PolarPlot, rysująca wykres we współrzędnych biegunowych
zapisalibyśmy Pierwiastki[a_, b_, c_]:= Roots[a*x^2+b*x+c==0, x] (wbudowana funkcja Roots rozwiązuje równania wielomianowe), a następnie użyli na przykład tak: Pierwiastki[2,0, -m]. W linii numer 3 najważniejsza jest funkcja PolarPlot, rysująca wykres we współrzędnych biegunowych ![|[a,b]∋ t ( (r(t),t),](/math/temat/informatyka/2019/05/29/Alchemia/8x-53f3f8c9f248c580c76c1684747d6b333462e62a-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie  jest długością promienia wodzącego, a
jest długością promienia wodzącego, a 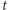 jest kątem, jaki tworzy z osią
jest kątem, jaki tworzy z osią 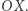 Najprostsze jej wywołanie w tym kontekście miałoby postać PolarPlot[ r[t], t, a, b ]. W naszym kodzie dodatkowo zmieniamy pewne opcje tej funkcji, korzystając z operatora nadawania wartości "->":
Najprostsze jej wywołanie w tym kontekście miałoby postać PolarPlot[ r[t], t, a, b ]. W naszym kodzie dodatkowo zmieniamy pewne opcje tej funkcji, korzystając z operatora nadawania wartości "->":

powodując, że w tytule wykresu są wypisywane wartości parametrów 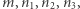 a osie współrzędnych nie będą rysowane.
a osie współrzędnych nie będą rysowane.
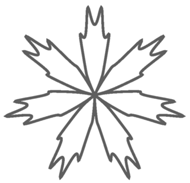
Jedna z nieskończenie wielu form, których nie było w artykule Gielisa: 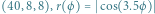
Aby mieć możliwość interaktywnego zmieniania wartości argumentów funkcji S innych niż t, zanurzamy wywołanie PolarPlot w funkcji Manipulate, która automatycznie stworzy okno z suwakami odpowiadającymi wartościom podanym jako dalsze jej argumenty. Przykładowo, podając (zob. w trzecim wierszu trzeciej linii kodu) {{a, 1}, 0, 5}, instruujemy Manipulate, że parametr 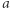 może przyjmować wartości z przedziału
może przyjmować wartości z przedziału ![|[0,5],](/math/temat/informatyka/2019/05/29/Alchemia/2x-a5e86cadb5faf7db4c39d19cd3f51f6256d1c47d-im-33,33,33-FF,FF,FF.gif) z domyślnie ustawioną wartością równą 1. Nieco bardziej złożony argument {{m, 4}, 0, 20, 1} oznacza, że
z domyślnie ustawioną wartością równą 1. Nieco bardziej złożony argument {{m, 4}, 0, 20, 1} oznacza, że 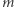 będzie domyślnie równe 4, będzie miało wartości z zakresu od 0 do 20, ale zmiana
będzie domyślnie równe 4, będzie miało wartości z zakresu od 0 do 20, ale zmiana 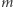 będzie odbywać się ze skokiem co 1 - dzięki czemu
będzie odbywać się ze skokiem co 1 - dzięki czemu 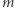 będzie przyjmować tylko całkowite wartości. Teraz możemy zacząć zabawę z suwakami i śledzić na bieżąco, jak zmiany parametrów wpływają na zmiany kształtu krzywej. Na marginesie powyżej pokazano te efekty działania superformuły, które są zbliżone do naturalnych kształtów i które tak zachwyciły Gielisa. Parametry w postaci
będzie przyjmować tylko całkowite wartości. Teraz możemy zacząć zabawę z suwakami i śledzić na bieżąco, jak zmiany parametrów wpływają na zmiany kształtu krzywej. Na marginesie powyżej pokazano te efekty działania superformuły, które są zbliżone do naturalnych kształtów i które tak zachwyciły Gielisa. Parametry w postaci 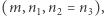 z "biologicznymi" interpretacjami, pochodzą z artykułu Gielisa w American Journal of Botany 90(3) z 2003 roku. Czy obrazki są ładne? Niewątpliwie. Ale czy jest w nich coś głębszego? Na to pytanie nie podam odpowiedzi: przecież alchemia to wiedza tajemna.
z "biologicznymi" interpretacjami, pochodzą z artykułu Gielisa w American Journal of Botany 90(3) z 2003 roku. Czy obrazki są ładne? Niewątpliwie. Ale czy jest w nich coś głębszego? Na to pytanie nie podam odpowiedzi: przecież alchemia to wiedza tajemna.
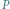 ma współrzędne biegunowe
ma współrzędne biegunowe 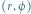
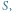 które generują kształty podobne do tych na ikonie Mathematiki powyżej?
które generują kształty podobne do tych na ikonie Mathematiki powyżej?