Deterministyczny automat skończony ma zbiór stanów 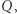z których jeden jest początkowy, a niektóre są akceptujące. Taki automat czyta słowo wejściowe od lewej do prawej. Zaczyna przed pierwszą literą i jest wtedy w stanie początkowym. Następnie, w zależności od litery w słowie, którą aktualnie widzi i stanu, w którym jest, uaktualnia swój stan i przesuwa się w prawo po słowie. Jeśli po przeczytaniu ostatniej litery automat znajduje się w stanie akceptującym, to akceptuje słowo wejściowe, a w przeciwnym razie je odrzuca.

Przykładowo automat może akceptować słowa, których długość przystaje do 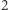modulo 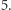Wówczas naturalnym zbiorem stanów jest 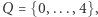stan początkowy to 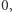a stan akceptujący jest tylko jeden, mianowicie 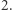Automat, niezależnie od litery w słowie, przechodzi ze stanu 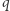do stanu 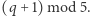Inny automat akceptuje słowa nad 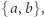które na pozycjach przystających do 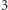modulo 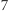mają w sumie parzyście wiele liter 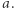Pamięta on, jaka jest reszta modulo 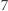aktualnej pozycji oraz jaka jest parzystość liczby 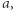które do tej pory widział na interesujących go pozycjach. A zatem zbiór stanów to 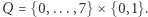Stan początkowy to 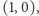bo zaczynamy od litery na pozycji 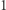i bez zobaczonych 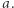Stany akceptujące to wszystkie postaci 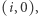gdyż akceptujemy, gdy liczba 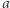na istotnych pozycjach jest parzysta, niezależnie od tego, jaka jest długość słowa. Jeśli automat widzi 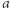w stanie 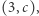to przechodzi do 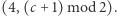W przeciwnym przypadku automat, niezależnie od tego, co widzi, przechodzi ze stanu 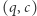do 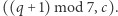Taki automat nazwiemy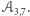

Możemy już sformułować problem rozróżniania słów. Pyta on, jakie jest takie minimalne 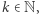że dla każdych dwóch różnych słów 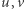o długości co najwyżej istnieje automat o co najwyżej 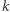stanach, który rozróżnia 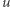i 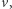tj. jedno z nich akceptuje, a drugie odrzuca.

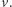Zauważmy najpierw, że, oczywiście, istnieje pewien taki automat. Istotnie, łatwo skonstruować automat, który akceptuje tylko słowo a więc odrzuca A zatem pytanie o najmniejszy taki automat ma w ogóle sens. Powyższy automat ma jednak 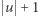stanów, czyli pesymistycznie 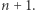Problem rozróżniania słów został postawiony w 1986 roku przez Goralčika i Koubeka, którzy pokazali, że zawsze da się stworzyć automat wielkości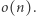

Zauważmy najpierw, że rozróżnianie słów i różnej długości jest stosunkowo proste. Wtedy wystarczy, by automat obliczał długość słowa modulo pewna liczba wielkości 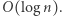Nietrudno to udowodnić, a jeszcze prościej uwierzyć. Istotnie, aby 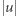i 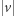dawały te same reszty modulo wszystkie liczby 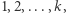to liczba 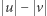musi dzielić się przez 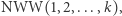co, jak dość łatwo wykazać, jest wykładnicze względem 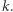Zatem do rozróżnienia wystarczy 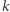rzędu 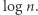Okazuje się też, że jeśli umiemy rozróżniać słowa nad alfabetem dwuliterowym, powiedzmy 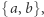to umiemy rozróżniać słowa nad dowolnym skończonym alfabetem automatami tej samej wielkości.

Niestety, dla słów i równej długości, nawet nad alfabetem 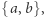nie jest już tak prosto. Najmocniejszy obecnie jest rezultat Robsona z 1989 roku, który pokazał, że dowolne dwa słowa da się rozróżnić pewnym automatem wielkości 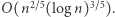Przy tym nie są znane pary słów, które rzeczywiście wymagają tak dużych automatów. Najtrudniejsze znane przykłady potrzebują jedynie automatów wielkości rzędu 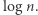A więc wciąż możliwe jest, że każde dwa słowa, nawet tej samej długości, da się rozróżnić automatem wielkości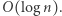

Ciekawy jest trochę późniejszy wynik Robsona, z 1996 roku. Pokazał on, że każde dwa różne słowa równej długości nad alfabetem 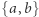można rozróżnić automatem 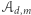dla 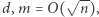podobnym do przedstawionego wyżej 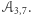Akceptuje on słowa mające na pozycjach przystających do 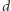modulo parzyście wiele liter 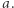To daje ograniczenie 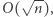gorsze od 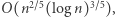ale za to rozważane automaty są bardzo proste.

Od 1996 roku nie ma żadnych postępów w tej sprawie. Amerykański informatyk, pracujący teraz w Waterloo, Jeffrey Shallit, zaoferował w 2014 roku nagrodę 100 funtów brytyjskich każdemu, kto poprawi wynik Robsona z 1989 roku. Warto podkreślić, że rozróżnianie słów jest problemem zupełnie innego kalibru niż izomorfizm grafów i mnożenie macierzy. Moim zdaniem jest to problem potencjalnie w zasięgu pasjonata informatyki bez wielkiego doświadczenia w badaniach. Dodatkowo jest on elegancko sformułowany, jego rozwiązanie może przynieść nowe metody lub zrozumienie głębszych zagadnień, a luka między 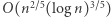a jest intrygująca. Dlatego zachęcam Czytelników Żądnych Wyzwań do przyjrzenia się sprawie.