Jak definiować ciągi rekurencyjne?
Tytułowa rekurencja jest jednym z podstawowych pojęć w informatyce, które umożliwia definiowanie ciągów różnych obiektów, pozwalając odwoływać się w definicji danego obiektu do jego poprzedników. Pokażemy dwie klasy takich definicji i omówimy ich równoważność.

Zacznijmy od prostych przykładów: ciągu arytmetycznego i ciągu geometrycznego. Rozważmy dwa ciągi 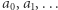 i
i 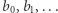 zadane przez
zadane przez
 |
(Takie ciągi przydają się, na przykład, do szacowania, jak długo działa program, który rekurencyjnie wywołuje siebie lub inne programy.)
W obu przypadkach, żeby poznać wartość konkretnego 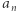 lub
lub 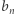 (korzystając wprost z definicji), trzeba się wciąż odwoływać do wartości poprzednich elementów, aż dojdziemy do pierwszego elementu
(korzystając wprost z definicji), trzeba się wciąż odwoływać do wartości poprzednich elementów, aż dojdziemy do pierwszego elementu 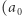 lub
lub  Oczywiście,
Oczywiście,  jest ciągiem arytmetycznym, a
jest ciągiem arytmetycznym, a  ciągiem geometrycznym, więc wiemy, że procedurę obliczania wartości konkretnego elementu ciągu da się przyspieszyć i skorzystać ze wzorów:
ciągiem geometrycznym, więc wiemy, że procedurę obliczania wartości konkretnego elementu ciągu da się przyspieszyć i skorzystać ze wzorów: 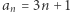 oraz
oraz 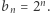 Nie zawsze jest to takie proste. Trochę ciekawszym przykładem jest ciąg Fibonacciego zadany przez:
Nie zawsze jest to takie proste. Trochę ciekawszym przykładem jest ciąg Fibonacciego zadany przez:
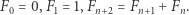 |
Zauważmy, że aby obliczyć wartości kolejnych elementów ciągu, musimy się zawsze odwołać do dwóch poprzednich elementów i dlatego potrzebne są aż dwa początkowe elementy. Spróbujmy uogólnić to zjawisko i zdefiniować tak zwane liniowe ciągi rekurencyjne, którym będziemy się dalej szerzej przyglądać. Powiemy, że ciąg 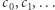 jest liniowym ciągiem rekurencyjnym stopnia
jest liniowym ciągiem rekurencyjnym stopnia 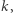 jeśli znamy wartości pierwszych
jeśli znamy wartości pierwszych 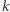 elementów, a pozostałe elementy są wyznaczone przez
elementów, a pozostałe elementy są wyznaczone przez 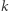 poprzednich elementów. Dokładniej:
poprzednich elementów. Dokładniej:
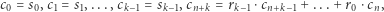 |
(1) |
dla danych liczb rzeczywistych 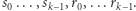 Dodatkowo zakładamy, że
Dodatkowo zakładamy, że  (inaczej ciąg byłby stopnia
(inaczej ciąg byłby stopnia 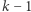 ). Przykładowo ciąg
). Przykładowo ciąg  jest takim ciągiem stopnia 1 i podobnie
jest takim ciągiem stopnia 1 i podobnie 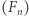 jest takim ciągiem stopnia 2. Ciąg
jest takim ciągiem stopnia 2. Ciąg 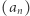 nie spełnia tej definicji, ponieważ
nie spełnia tej definicji, ponieważ 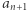 odwołuje się do stałej
odwołuje się do stałej 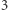 (zauważmy, że w definicji (1) stałe
(zauważmy, że w definicji (1) stałe 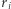 mogą być tylko przemnożone przez jeden z poprzednich elementów ciągu
mogą być tylko przemnożone przez jeden z poprzednich elementów ciągu 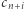 ). Można to jednak łatwo naprawić: zauważmy, że ciąg
). Można to jednak łatwo naprawić: zauważmy, że ciąg 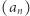 spełnia
spełnia  Tak więc wystarczy w definicji podmienić trójkę na
Tak więc wystarczy w definicji podmienić trójkę na 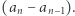 Otrzymujemy w ten sposób równoważną rekurencję stopnia 2:
Otrzymujemy w ten sposób równoważną rekurencję stopnia 2:
 |
Pierwsze pytanie, jakim się zajmiemy w tym tekście, to pytanie, czy możemy ograniczyć się wyłącznie do ciągów stopnia 1. Okazuje się, że odpowiedź brzmi "tak", ale - niestety - nie za darmo. Jeśli pozwolimy na to, żeby użyć więcej niż jednego ciągu, to każdy ciąg stopnia 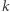 można zamienić na układ
można zamienić na układ 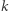 ciągów stopnia 1. Przykładowo ciąg Fibonacciego można zdefiniować, używając jednego dodatkowego ciągu:
ciągów stopnia 1. Przykładowo ciąg Fibonacciego można zdefiniować, używając jednego dodatkowego ciągu:
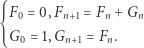 |
Nietrudno zauważyć, że ciąg 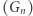 służy jako bufor do przetrzymywania wartości
służy jako bufor do przetrzymywania wartości 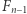 i równie nietrudno uogólnić tę metodę na dowolny ciąg stopnia
i równie nietrudno uogólnić tę metodę na dowolny ciąg stopnia 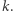 W takim razie zadajmy pytanie odwrotne: czy mając układ
W takim razie zadajmy pytanie odwrotne: czy mając układ 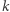 ciągów stopnia 1, możemy zdefiniować każdy ciąg z tego układu za pomocą jednego ciągu (być może stopnia większego niż 1)? Rozważmy przykład, który pokaże trudność tego zadania: zdefiniujemy ciąg
ciągów stopnia 1, możemy zdefiniować każdy ciąg z tego układu za pomocą jednego ciągu (być może stopnia większego niż 1)? Rozważmy przykład, który pokaże trudność tego zadania: zdefiniujemy ciąg 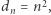 używając dwóch dodatkowych ciągów:
używając dwóch dodatkowych ciągów:  i
i 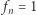
 |
(2) |
Poprawność tej definicji wynika z prostej tożsamości 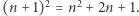 Czy możemy zdefiniować ciąg
Czy możemy zdefiniować ciąg 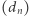 bez użycia dodatkowych ciągów? Warto się chwilę zastanowić nad tym pytaniem, zanim przeczytamy rozwiązanie. Odpowiedź brzmi "tak" i realizuje ją rekurencja poniżej:
bez użycia dodatkowych ciągów? Warto się chwilę zastanowić nad tym pytaniem, zanim przeczytamy rozwiązanie. Odpowiedź brzmi "tak" i realizuje ją rekurencja poniżej:
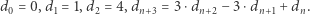 |
(3) |
Szybkie rachunki pokazują poprawność tego wzoru
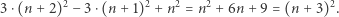 |
(4) |
Ogólnie prawdą jest, że każdy ciąg zdefiniowany za pomocą układu 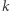 ciągów stopnia 1 możemy przekształcić w ciąg zdefiniowany za pomocą tylko jednego ciągu o stopniu
ciągów stopnia 1 możemy przekształcić w ciąg zdefiniowany za pomocą tylko jednego ciągu o stopniu 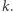 Dowód tego faktu nie jest bardzo trudny, ale wymaga podstawowej znajomości algebry liniowej, więc nie omówimy go tutaj w pełnej ogólności.
Dowód tego faktu nie jest bardzo trudny, ale wymaga podstawowej znajomości algebry liniowej, więc nie omówimy go tutaj w pełnej ogólności.
Zamiast tego spróbujemy zademonstrować tę własność dla szczególnego przypadku. Zauważmy, że nietrudno uogólnić definicję (2) tak, żeby zdefiniować 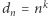 dla dowolnego
dla dowolnego 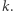 Wystarczy rozpisać wzór na
Wystarczy rozpisać wzór na 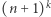 i użyć
i użyć 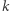 dodatkowych ciągów. Wykażemy, że można ten ciąg zdefiniować, używając tylko jednego ciągu stopnia
dodatkowych ciągów. Wykażemy, że można ten ciąg zdefiniować, używając tylko jednego ciągu stopnia 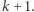 Pierwsze
Pierwsze 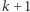 elementów zadajemy w oczywisty sposób jako:
elementów zadajemy w oczywisty sposób jako:

Rekurencję weźmiemy trochę "z kapelusza". Najpierw rozwiniemy wielomian w równaniu 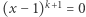 :
:
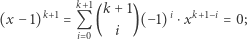 |
(5) |
i przeniesiemy wszystkie wyrazy o stopniu mniejszym niż 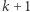 na prawą stronę
na prawą stronę
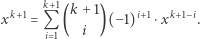 |
(6) |
Z tego wzoru magicznie otrzymujemy wzór rekurencyjny na 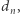 podstawiając
podstawiając 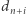 pod jednomian
pod jednomian 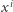 dla każdego
dla każdego 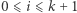 (w szczególności pod
(w szczególności pod 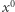 podstawiamy
podstawiamy 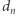 ):
):
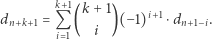 |
Sprawdźmy, że dla 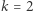 dostajemy
dostajemy 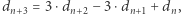 czyli dokładnie rozwiązanie z (3). Pozostaje wykazać, że rekurencja otrzymana z (6) jest poprawna dla każdego
czyli dokładnie rozwiązanie z (3). Pozostaje wykazać, że rekurencja otrzymana z (6) jest poprawna dla każdego  Wystarczy sprawdzić, że
Wystarczy sprawdzić, że
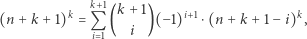 |
czyli
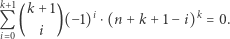 |
(7) |

Uzasadnimy to równanie, korzystając z metody interpretacji kombinatorycznej. Otóż dla ustalonej wartości 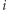 rozważmy
rozważmy 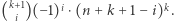 Przyjmijmy, że mamy dwie grupy elementów: pierwszą grupę
Przyjmijmy, że mamy dwie grupy elementów: pierwszą grupę 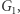 gdzie
gdzie  ; i drugą
; i drugą 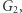 gdzie
gdzie  Możemy zinterpretować
Możemy zinterpretować 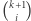 jako wybranie podzbioru
jako wybranie podzbioru 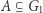 o rozmiarze
o rozmiarze 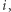 natomiast
natomiast 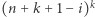 jako dobranie ciągu z powtórzeniami
jako dobranie ciągu z powtórzeniami 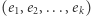 spośród pozostałych elementów, czyli
spośród pozostałych elementów, czyli  Pozostały czynnik
Pozostały czynnik 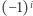 określa, czy to wszystko dodamy, czy odejmiemy od całej sumy.
określa, czy to wszystko dodamy, czy odejmiemy od całej sumy.
Obliczymy teraz to samo raz jeszcze, ale tym razem w innej kolejności. Ustalmy najpierw jakiś ciąg z powtórzeniami 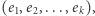 gdzie
gdzie 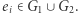 Niech
Niech 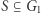 będzie zbiorem elementów, które nie występują w ciągu
będzie zbiorem elementów, które nie występują w ciągu  i oznaczmy
i oznaczmy  Pytanie brzmi, na ile różnych sposobów można dobrać do tego ciągu zbiór
Pytanie brzmi, na ile różnych sposobów można dobrać do tego ciągu zbiór  tak, żeby otrzymać dokładnie to samo co poprzednio. Jedyny warunek, jaki
tak, żeby otrzymać dokładnie to samo co poprzednio. Jedyny warunek, jaki  musi spełniać, to
musi spełniać, to  Przyjmijmy dodatkowo, że chcemy wybrać
Przyjmijmy dodatkowo, że chcemy wybrać  ustalonego rozmiaru
ustalonego rozmiaru 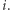 Możemy to zrobić na
Możemy to zrobić na 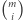 sposobów i wtedy będziemy brali ten składnik ze znakiem
sposobów i wtedy będziemy brali ten składnik ze znakiem 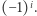 To znaczy, że dla ustalonego ciągu
To znaczy, że dla ustalonego ciągu 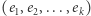 dodamy do sumy
dodamy do sumy 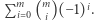 Podstawiając w (5)
Podstawiając w (5) 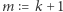 oraz
oraz 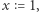 widzimy, że to wyrażenie jest zawsze równe
widzimy, że to wyrażenie jest zawsze równe 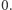 To znaczy, że sumując po wszystkich ciągach
To znaczy, że sumując po wszystkich ciągach 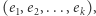 otrzymamy i tak
otrzymamy i tak  czyli wykazaliśmy (7).
czyli wykazaliśmy (7).
Nasz argument, niestety, wymagał wyczarowania rekurencji otrzymanej z rozpisania (5). Żeby otrzymać ten wzór bez zgadywania, potrzeba ponownie nieco algebry liniowej. Co więcej, zauważmy, że nawet samo udowodnienie poprawności tego wzoru wymagało znajomości podstaw kombinatoryki. Niech będzie to więc przestroga, że i informatykowi dobrze jest znać trochę matematyki.