Modelowanie stosuje się również w wielu innych przypadkach, gdy chcemy przewidzieć w sposób przybliżony, co będzie w przyszłości. Konstruuje się modele opisujące ceny akcji na giełdzie, wielkość pokrywy lodowej w Arktyce, erupcje wulkanów, wielkość populacji danego kraju czy świata, ewolucję chorób na danym terenie itd. We wszystkich tych sytuacjach chcemy czegoś dowiedzieć się o przyszłości ważnego dla nas zjawiska czy procesu, ale jest on na tyle skomplikowany, że nie jesteśmy w stanie zrobić tego dokładnie. Dlatego idziemy na kompromis i zajmujemy się pewnym przybliżeniem rzeczywistości. Będzie to, co prawda, przybliżenie, ale za to będziemy w stanie z nim pracować i rzeczywiście obliczać, jak się ono zachowa w przyszłości. Modele rzeczywistości mogą być dosyć dokładne, wtedy jednak (ze względu na złożoność) ciężko analizować ich własności i obliczać, jak będą ewoluowały. Ale za to, jeśli to już zrobimy, będziemy mieli dobre przybliżenie tego, co się stanie naprawdę. Mogą być też mniej dokładne, wtedy będą zachowywały się istotnie inaczej niż rzeczywistość. W zamian za to będzie nam je łatwiej analizować, a analiza przyniesie pewne wnioski, które choć częściowo pozwolą zrozumieć badane zjawisko.

Czasem model, który tworzymy, wcale niekoniecznie ma wiele wspólnego z rzeczywistością, ale konstruujemy go tak, by dawał dobre wyniki dla niektórych eksperymentów, mając nadzieję, że przyda nam się on do przewidywania wyników innych eksperymentów. Ten sposób patrzenia na modelowanie bliższy jest fizyce, gdzie siłą rzeczy nie znamy istoty rzeczywistości, więc możemy jedynie konstruować model tak, by dobrze przybliżał znane nam obserwacje. Dobrymi przykładami są tu: kopernikański model układu słonecznego czy model standardowy opisujący świat w mikroskali.

Skoro modelowanie stosuje się w ekonomii, meteorologii, biologii, fizyce, socjologii, to dlaczego by nie zastosować go w informatyce do lepszego badania zachowań programów? Istotnie się to robi i modele programów mają sporo różnych zastosowań. W informatyce znamy zasady kierujące działaniem programów, natomiast nie umiemy przewidywać, do czego doprowadzą. Dlatego stosujemy podejście, w którym budowany model odzwierciedla rzeczywistość w sposób przybliżony. Jednym z ważnych zastosowań jest automatyczna weryfikacja programów, czyli automatyczne wykrywanie błędów w programach. Oczywiście, nie jest ono zupełnie automatyczne, ale jego część wykonuje się automatycznie. Chcemy wykryć, czy nasz program może potencjalnie wykonać pewnego rodzaju błędny przebieg. Powiedzmy, pytamy, czy może on w pewnym momencie próbować podzielić coś przez 0. W tym celu konstruuje się model programu 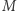i opisuje w precyzyjny sposób, co rozumiemy przez błędny przebieg. W naszej sytuacji byłby to ciąg instrukcji, który kończy się instrukcją: podziel coś przez 0. Takie błędne ciągi instrukcji charakteryzuje się przy użyciu formuł pewnych logik. Powiedzmy, że formuła logiczna 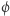opisuje ciągi instrukcji kończące się podzieleniem przez 0, to znaczy wylicza się do prawdy przy podstawieniu takich ciągów, a do fałszu przy pozostałych. Teraz wystarczy już tylko sprawdzić, czy w modelu 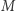możliwe jest obliczenie, dla którego formuła 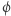zwraca wartość prawda. To podejście nazywa się z angielska model checking, czyli sprawdzanie modelu, i cieszy się dużym sukcesem komercyjnym. Dla przykładu, firma Intel wydaje na rozwój tej techniki miliony dolarów.

Jednak korzyść z analizowania modeli programów nie jest tylko komercyjna, ale również teoretyczna. Jednym z modeli programów, bardzo dokładnym i skomplikowanym, jest maszyna Turinga. Dzięki temu, że ustalony został precyzyjny model programu, można zdefiniować, co dokładnie oznacza, że dany problem da się rozwiązać w czasie wielomianowym albo że jest w klasie NP, wielokrotnie wspominanej na łamach Delty. Czyli właściwe definicje modeli pomagają nam lepiej zrozumieć świat programów, powiązania między różnymi pojęciami, a często także pozwalają opracować szybkie algorytmy.

Żeby przejść do konkretów, przyjrzyjmy się najprostszemu modelowi programu, mianowicie automatowi skończonemu. Dowolny program w każdej chwili swojego działania jest w jakimś stanie pamięci. Przykładowo, program szukający maksimum w tablicy o rozmiarze 100 może być w stanie: jestem w 37 komórce tablicy, do tej pory największa liczba to 178, a aktualnie spoglądam na liczbę 110. Przy praktycznym założeniu, że każdy komputer ma skończoną pamięć, liczba możliwych stanów programu jest również skończona. Natomiast obliczenie programu polega na przechodzeniu pomiędzy tymi stanami według pewnego ustalonego zestawu reguł (ten zestaw, oczywiście, zależy od programu). Nasz program szukający maksimum może przejść np. do stanu: jestem w 38 komórce tablicy, największa znaleziona liczba to 178, aktualnie widzę liczbę 88. Dodatkowo zmiany stanu programu mogą być różnych typów - w naszym przykładzie jest to uaktualnienie maksimum albo przejście dalej w prawo w tablicy. Model powinien to móc uwzględniać. Dodatkowo model powinien zawierać informację, w jakim stanie program zaczyna swoje działanie oraz w jakich stanach się kończy. Sprecyzujmy teraz opisane intuicje i zdefiniujmy dokładnie, czym jest automat skończony.

Deterministyczny automat skończony 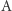nad skończonym alfabetem 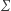składa się ze zbioru stanów 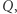wyróżnionego stanu początkowego 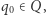zbioru stanów akceptujących 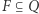oraz zbioru tranzycji 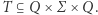Jeśli dla pewnych stanów 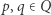oraz litery 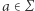zachodzi 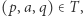to piszemy 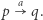Biegiem automatu 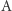po słowie 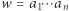składającym się z liter 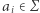nazwiemy ciąg takich stanów 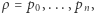że 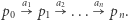Jeśli dodatkowo 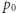jest stanem początkowym, a 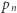pewnym stanem akceptującym, to bieg 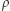nazwiemy akceptującym i powiemy, że słowo jest akceptowane przez automat. Natomiast językiem rozpoznawanym przez automat 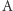nazywamy zbiór wszystkich słów przez niego akceptowanych. Intuicyjnie język automatu 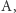oznaczany 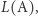opisuje zbiór wszystkich ciągów akcji programu, który modeluje dany automat. Jeśli słowo 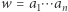należy do 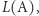to oznacza, że w programie jest pewien przebieg, w którym po kolei program wykonuje akcje typu 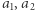itd. aż na końcu wykonuje akcję typu 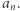Stan natomiast intuicyjnie reprezentuje to, co w danym momencie trzeba pamiętać o prefiksie słowa, żeby pod koniec stwierdzić, czy całe słowo należy do języka, czy też nie.

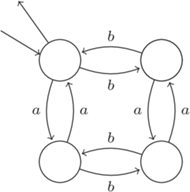
Automat rozpoznający język słów nad alfabetem 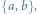które zawierają parzyście wiele liter oraz parzyście wiele liter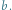

Okazuje się, że automaty skończone przydatne są nie tylko do modelowania działania programów, ale są po prostu bardzo eleganckim pojęciem, które jest użyteczne w wielu kontekstach. Przykładowo, znajdują zastosowanie przy sprawdzaniu, czy model 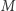spełnia formułę 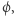albo przy analizie algorytmów operujących na znanych niektórym Czytelnikom wyrażeniach regularnych. Wyrażenia regularne są zbudowane przy użyciu sumy (oznaczanej 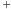), konkatenacji (oznaczanej ) i gwiazdki (oznaczanej ). 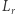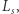Jeśli i opisują języki oraz to 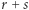opisuję sumę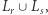 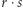opisuje język słów, których pierwsza część należy do 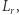a druga do 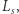natomiast 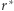opisuje język słów, które dadzą się podzielić na skończenie wiele części, z których każda należy do 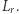Przykładowo wyrażenie 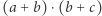opisuje język czterech słów, których pierwsza litera to lub 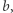a druga to 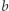lub 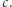Natomiast wyrażenie 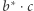opisuje język nieskończenie wielu słów, które zaczynają się pewną liczbą liter 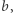a kończą się literą Okazuje się, że język automatu na rysunku również da się opisać wyrażeniem regularnym:

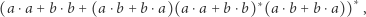
zachęcamy Czytelników do uzasadnienia tego faktu. Co ciekawe, wyrażenia regularne opisują tak naprawdę dokładnie te same języki, co automaty skończone. To jednak temat na zupełnie inną opowieść.