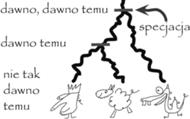
Drzewo gatunków dla króla Kraka, owcy domowej i smoka wawelskiego. Poziome kreski to specjacje.

Geny zmieniały się - niektóre były powielane, a niektóre stawały się bezużyteczne i były tracone. W tych czasach Ziemia miała tylko jeden kontynent, który z czasem uległ rozpadowi, dzieląc organizmy na nim żyjące. Część z organizmów wyginęła, a pozostałe powoli ewoluowały, dostosowując się do warunków panujących na nowych kontynentach. Te drobne zmiany, kumulowane przez tysiące rozdzielonych pokoleń, spowodowały, że gatunki niegdyś mające tych samych przodków stawały się zupełnie odmienne na różnych kontynentach. To zjawisko wykształcania się nowych gatunków nazywać będziemy specjacją.

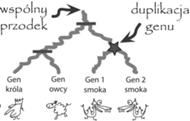
Drzewo łatwej rodziny genów, gdzie smok ma dwie kopie genu. Szybko zauważamy, że wystarczy jedna duplikacja genu, by uzgodnić to drzewo genów do drzewa gatunków smoka i jego ewolucyjnych kuzynów. Poziome kreski oznaczają węzły pasujące do specjacji z drzewa gatunków.

W tej historii mamy gatunek i gen, które związane są relacją gatunek ma geny, oraz kilka zjawisk takich jak duplikacja genu, strata genu oraz specjacja gatunku. Ich własności przedstawimy dokładniej na kilku przykładach.

Związki między gatunkami przedstawia się za pomocą ukorzenionego drzewa, nazywanego drzewem gatunków, którego węzły wewnętrzne są specjacjami, a liście to gatunki. Zilustrujemy to na przykładzie. Naszym drzewem gatunków będzie drzewo z reprezentantami trzech gatunków: królem Krakiem, owcą i smokiem wawelskim. Król i owca, jako bliżej spokrewnione, będą w naszym drzewie gatunków umieszczone obok siebie. Inaczej można powiedzieć, że ich rozdzielenie (specjacja) nastąpiło później niż rozdzielenie np. smoka i owcy.

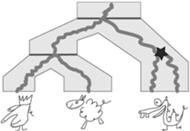
Uzgadnianie: wbudowanie drzewa łatwej rodziny genów w drzewo gatunków. Drzewo genów jest "rozciągane" tak by umieścić je wewnątrz drzewa gatunków.

Podobnie można reprezentować relacje między genami. Klasycznym przykładem są białka nazywane globinami, które m.in. wchodzą w skład cząsteczki hemoglobiny odpowiedzialnej za transport tlenu w naszych organizmach. Globiny występują w wielu organizmach, a ich sekwencje są zapisane w genach zazwyczaj występujących w kilku wariantach. Zakłada się, że globiny pochodzą od wspólnego przodka (genu). To założenie pozwala zgrupować geny globin w rodzinę i wizualizować relacje między nimi za pomocą drzewa genów, które można obliczyć z sekwencji za pomocą programów komputerowych. Dla ustalonego zbioru gatunków liczba różnych rodzin genów mających wspólnego przodka może wynosić nawet kilkanaście tysięcy.

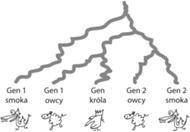
Drzewo trudnej rodziny genów, gdzie jeden gen pochodzi od króla, a po 2 od smoka i owcy. Dopasowanie tego drzewa genów do drzewa gatunków jest trudniejsze niż w poprzednim przypadku. Ile potrzeba duplikacji i gdzie je umieścić? Czy potrzebujemy innych zdarzeń (np. strat genów)?

Zjawiska ewolucyjne takie jak duplikacje genów, straty i specjacje (a także kilka innych, o których tutaj nie będziemy opowiadać), powodują, że drzewa rodzin genów i drzewa ich gatunków mogą się różnić. Niektóre przypadki są dość proste, tak jak łatwa rodzina genów z naszego przykładu. Tutaj wystarczy użyć jednej duplikacji genu i drzewo genów zostanie uzgodnione z drzewem gatunków. Można powiedzieć, że uzgadnianie drzew polega na narysowaniu drzewa genów wewnątrz drzewa gatunków, tak by zachować poprawność biologiczną i tak by minimalizować liczbę duplikacji genów.

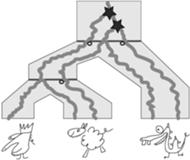
Uzgadnianie: wbudowanie drzewa trudnej rodziny genów w drzewo gatunków. Miejsca duplikacji genów są oznaczone gwiazdką. Dodatkowo można wyznaczyć liczbę strat genów (tutaj 3), które są konieczne do uzgodnienia drzew.

W trudnej rodzinie genów podobnie obserwujemy różnice w ilości kopii genów występujących w gatunkach. Można je wyjaśnić duplikacjami, ale to drzewo genów ma tak wymieszane etykiety, że uzgadnianie nie jest tak oczywiste jak w poprzednim przypadku. Stosując zasadę wbudowywania drzewa genów w drzewo gatunków, najpierw dla każdego węzła z drzewa genów określimy, gdzie ma być umieszczony w drzewie gatunków. Oczywiście, liście (geny) z drzewa genów muszą być umieszczone w odpowiednich liściach drzewa gatunków. Następnie mamy 4 węzły wewnętrzne: korzeń, prawy syn korzenia i dwóch wnuczków korzenia, czyli środkowy wnuczek (ojciec genu pierwszej owcy i genu króla) oraz prawy wnuczek (ojciec genów drugiej owcy i smoka). Z korzenia drzewa genów widoczne są wszystkie trzy gatunki, dlatego powinien on być umieszczony w korzeniu drzewa gatunków. To samo możemy powiedzieć o jego prawym synu. Środkowy wnuczek jest ojcem genów owcy i króla, dlatego umieścimy go na specjacji owcy i króla w drzewie gatunków. Ostatni węzeł, czyli prawy wnuczek korzenia, jest ojcem genów owcy i smoka. Z tego powodu nie możemy go umieścić w specjacji owcy i króla, bo brakuje tam smoka. Ostatecznym wyborem dla niego jest korzeń drzewa gatunków. Widzimy, że trzy węzły drzewa genów: korzeń, prawy syn i prawy wnuczek muszą być umieszczone w tym samym miejscu. To jednak nie jest możliwe, bo istnieje między nimi zależność czasowa: ojciec jest starszy od syna i w drzewie musi być umieszczony powyżej syna. Ten konflikt jest rozwiązywany przez "rozciągnięcie" tego fragmentu drzewa genów. W konsekwencji tylko prawy wnuczek zostanie umieszczony na węźle specjacji (korzeń drzewa gatunków), a jego ojciec i dziadek jako węzły duplikacji znajdą się nad nim, czyli nad specjacją. W tym przykładzie jest to jedyna konfliktowa sytuacja, dlatego wnioskujemy, że do uzgodnienia potrzeba dwóch duplikacji. Obrazek z uzgodnieniem tej trudnej rodziny genów drzew jest umieszczony obok.

Mapowanie najniższego wspólnego przodka (lca) pomiędzy drzewem trudnej rodziny genów i drzewem gatunków (dla czytelności narysowane tylko dla węzłów wewnętrznych). Tutaj to król, to owca, a to smok. W drzewie genów mamy dwa węzły duplikacyjne, które wyznaczamy za pomocą lca-mapowania zgodnie z zasadą: węzeł jest duplikacją jeśli jego mapowanie jest równe mapowaniu jego syna.

Z powyższego przykładu widzimy, że węzły duplikacji można wyznaczyć za pomocą mapowań najniższego wspólnego przodka (lca). Formalnie, lca-mapowanie to funkcja, która każdemu węzłowi 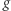z drzewa genów przyporządkowuje najniższy węzeł z drzewa gatunków, tak by zbiór gatunków widoczny z 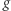był widoczny z Zwróćmy uwagę, że jest to zgodne z postępowaniem, które zastosowaliśmy w poprzednim przykładzie. Teraz możemy powiedzieć, że węzeł z drzewa genów jest duplikacją, jeśli jego mapowanie jest równe mapowaniu jednego z jego synów. Przykład lca-mapowania dla trudnej rodziny genów wraz z oznaczeniem duplikacji jest zilustrowany na obrazku.

Oprócz duplikacji można także policzyć straty genów. W uzgadnianiu straty genów występują, gdy po specjacji jeden z gatunków traci gen. Łatwo je wyznaczymy, jeśli narysujemy wbudowanie drzewa genów w drzewo gatunków. W takim przypadku strata genu występuje, gdy krawędź drzewa genów przecina specjację. Zauważmy, że łatwa rodzina genów nie generuje strat, bo na specjacjach we wbudowaniu znajdują się wyłącznie węzły wewnętrzne drzewa genów. W przypadku trudnej rodziny mamy 3 straty genów.

Interesującym zastosowaniem uzgadniania może być zagadnienie obliczenia Drzewa Życia, czyli drzewa wszystkich żyjących gatunków na Ziemi. Ten problem jest instancją problemu superdrzewa, który w kontekście uzgadniania definiujemy tak: dla kolekcji drzew genów znajdź drzewo gatunków minimalizujące całkowitą liczbę duplikacji. Zatem, by obliczyć Drzewo Życia, należy najpierw obliczyć drzewa rodzin genów pokrywające możliwie dużą liczbę gatunków. To samo w sobie jest dość skomplikowanym zadaniem, bo obecnie nie wszystkie gatunki są całkowicie zsekwencjonowane. Co więcej, w przeciwieństwie do uzgadniania, które można wykonać w czasie liniowym, problem superdrzewa jest złożony obliczeniowo (wersja decyzyjna jest w klasie NPC). Z tego powodu programy komputerowe rozwiązujące ten problem zwykle używają przybliżonych metod, które nie gwarantują znalezienia optymalnego drzewa. Mimo tych wad uzgadnianie, jako model biologicznie dobrze umotywowany, jest często stosowane m.in. do obliczania drzewa gatunków, w tym również Drzewa Życia.