Programowanie półcałkowitoliczbowe
W tym artykule zmierzymy się z problemem pokrycia wierzchołkowego (Vertex Cover). Poruszymy kilka kwestii na pograniczu optymalizacji liniowej, złożoności obliczeniowej oraz algorytmów parametryzowanych...
Większość Czytelników może znać ten problem z różnych źródeł (między innymi pojawiał się on już w Delcie przed laty), ale na wszelki wypadek na początek przypomnę definicję.
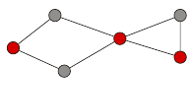
Rys. 1 Graf z zaznaczonym kolorem jego minimalnym pokryciem wierzchołkowym.
Definicja 1. Pokryciem wierzchołkowym grafu 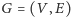 nazwiemy taki zbiór wierzchołków, że dla każdej krawędzi
nazwiemy taki zbiór wierzchołków, że dla każdej krawędzi  występującej w grafie, przynajmniej jeden z wierzchołków
występującej w grafie, przynajmniej jeden z wierzchołków 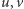 należy do pokrycia.
należy do pokrycia.
Minimalne pokrycie wierzchołkowe to, oczywiście, takie, które zawiera najmniejszą możliwą liczbę wierzchołków.
Z teorii złożoności wiemy już, że nasz problem jest NP-zupełny. Znaczy to, że jeśli potrafilibyśmy go szybko rozwiązać, to poprzez pewne redukcje umielibyśmy również szybko rozwiązać wszystkie problemy z klasy NP. W tym przypadku przez "szybko" rozumiemy rozwiązanie działające w czasie wielomianowym, czyli 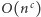 dla pewnej stałej
dla pewnej stałej 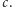 Jedna ze słynniejszych hipotez w informatyce mówi, że
Jedna ze słynniejszych hipotez w informatyce mówi, że 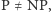 czyli że klasa problemów rozwiązywalnych w deterministycznym czasie wielomianowym jest mniejsza od tej rozpoznawanej w niedeterministycznym (czyli nie zachodzi
czyli że klasa problemów rozwiązywalnych w deterministycznym czasie wielomianowym jest mniejsza od tej rozpoznawanej w niedeterministycznym (czyli nie zachodzi  zawieranie
zawieranie 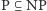 jest oczywiste). Przy założeniu, że hipoteza ta jest prawdziwa, problemów NP-zupełnych nie da się rozwiązywać w deterministycznym czasie wielomianowym.
jest oczywiste). Przy założeniu, że hipoteza ta jest prawdziwa, problemów NP-zupełnych nie da się rozwiązywać w deterministycznym czasie wielomianowym.
Jak możemy znaleźć minimalne pokrycie wierzchołkowe?
Pierwszym pomysłem, jaki możemy mieć, jest przejrzenie wszystkich podzbiorów wierzchołków naszego grafu i wybranie takiego, który jest pokryciem wierzchołkowym i ma najmniejszy rozmiar. Takich podzbiorów jest  (gdzie
(gdzie  to liczba wierzchołków w naszym grafie).
to liczba wierzchołków w naszym grafie).
Możemy też się zabrać za to inaczej - okazuje się, że bardzo często w problemach kombinatorycznych z pomocą przychodzi programowanie liniowe.
Tak też jest i w naszym przypadku. Dla każdego wierzchołka  w naszym grafie stworzymy zmienną całkowitą
w naszym grafie stworzymy zmienną całkowitą 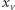 oznaczającą, czy bierzemy
oznaczającą, czy bierzemy  do naszego pokrycia, czy też nie. Oczywiście, będziemy chcieli zminimalizować liczbę wziętych wierzchołków. Wymaganie co do pokrycia krawędzi wyrazimy, tworząc dla każdej krawędzi
do naszego pokrycia, czy też nie. Oczywiście, będziemy chcieli zminimalizować liczbę wziętych wierzchołków. Wymaganie co do pokrycia krawędzi wyrazimy, tworząc dla każdej krawędzi 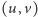 nierówność
nierówność 
Podsumowując powyższe, dostajemy następujący program liniowy całkowitoliczbowy:
Minimalizuj 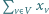 z zachowaniem warunków:
z zachowaniem warunków:
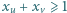 dla każdego
dla każdego 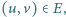
 dla każdego
dla każdego 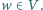
Potrafimy wyrazić więc problem NP-zupełny za pomocą ILP (Integer Linear Programming - programowanie całkowitoliczbowe). Oznacza to dokładnie, że pokazaliśmy w tym momencie NP-trudność problemu ILP. Tym samym nie oczekujemy, że dla ILP istnieje jakikolwiek algorytm działający w czasie wielomianowym.
Co się stanie, gdy zapomnimy o warunkach całkowitości dla naszych zmiennych?
Dostaniemy zwykły program liniowy, a przecież do rozwiązywania takiego istnieją już algorytmy wielomianowe! Pytanie, czy wyniki tego programu mogą się nam do czegoś przydać. Mogłoby się wydawać, że nie - przykładowo dla cyklu o 3 wierzchołkach optymalnym rozwiązaniem będzie dać 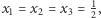 które nam za wiele nie mówi.
które nam za wiele nie mówi.
Okazuje się jednak, że ta forma programu liniowego może być dla nas wciąż użyteczna! W dziedzinie algorytmów parametryzowanych istnieje dział zwany kernelizacją. Wykorzystamy rozwiązanie naszego LP (Linear Programming) właśnie w procesie kernelizacji. Najpierw jednak może warto wspomnieć, co kryje się pod tajemniczymi hasłami użytymi powyżej.
W skrócie algorytmy parametryzowane to takie, w których wybieramy sobie parametr opisujący w pewien sposób instancję naszego problemu, a następnie względem tego parametru będziemy optymalizować prędkość działania naszego algorytmu. Parametry te mogą w najróżniejszy sposób opisywać problem, z którym się mierzymy. Oczywiście, podstawowym parametrem może być wielkość naszego problemu wejściowego, jednak dużo z takiego parametru raczej nie wyciągniemy. Sensowniejszym przykładem dla problemów grafowych może być, na przykład, maksymalny stopień wierzchołka w rozważanym grafie. W ogólności, do każdego problemu da się wymyślić dużo różnych parametrów, ale wybranie tego właściwego może okazać się sporym wyzwaniem.
Drugie tajemnicze słowo, czyli "kernelizacja", można przetłumaczyć jako znajdowanie jądra problemu - chcemy w szybkim czasie z jakiejś instancji problemu NP-zupełnego wydobyć jego najtrudniejszą obliczeniowo część. Dzięki temu bardzo często jesteśmy w stanie mocno ograniczyć rozmiary problemu, z którym się borykamy, co znacząco przyspieszy nasze obliczenia (zostanie nam dużo mniej zadań, które musimy przetworzyć w czasie wykładniczym). Aby rozjaśnić te pojęcia, za chwilę zilustrujemy je na przykładzie pokrycia wierzchołkowego.
Skupimy się tym razem na wersji decyzyjnej problemu pokrycia wierzchołkowego - czy dla danego grafu 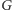 istnieje pokrycie zawierające co najwyżej
istnieje pokrycie zawierające co najwyżej 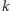 wierzchołków. Jako parametru użyjemy rozmiaru poszukiwanego rozwiązania (czyli liczby wierzchołków
wierzchołków. Jako parametru użyjemy rozmiaru poszukiwanego rozwiązania (czyli liczby wierzchołków 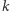 w pokryciu).
w pokryciu).
Używając rozwiązania naszego programu liniowego
Minimalizuj 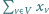 z zachowaniem warunku:
z zachowaniem warunku: 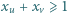 dla każdego
dla każdego 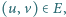
podzielimy wierzchołki na 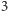 zbiory:
zbiory:
W tym momencie jasne się powinno stać, skąd w tytule wzięła się nazwa półcałkowite - przekształcamy rozwiązanie LP tak, żeby oprócz wartości całkowitych 0 i 1 osiągało ono trzecią wartość  Okazuje się, że taka postać rozwiązania jest niezwykle użyteczna w znajdowaniu jądra. Pierwszym spostrzeżeniem, jakie możemy poczynić, jest to, że jeśli spojrzymy na którykolwiek wierzchołek
Okazuje się, że taka postać rozwiązania jest niezwykle użyteczna w znajdowaniu jądra. Pierwszym spostrzeżeniem, jakie możemy poczynić, jest to, że jeśli spojrzymy na którykolwiek wierzchołek 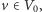 to musi mieć on sąsiada należącego do zbioru
to musi mieć on sąsiada należącego do zbioru  Można jednak udowodnić dużo ciekawsze twierdzenie.
Można jednak udowodnić dużo ciekawsze twierdzenie.
Twierdzenie 1 (Nemhausera-Trottera). Istnieje takie minimalne pokrycie wierzchołkowe 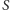 w grafie G, że:
w grafie G, że:
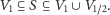
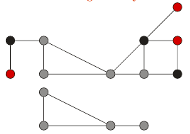
Rys. 2 U góry graf z odpowiednio zaznaczonymi kolorem wierzchołkami z 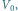 szaro z
szaro z 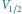 i czarno z
i czarno z 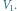 Na dole ten sam graf po wykonaniu na nim powyższej redukcji/
Na dole ten sam graf po wykonaniu na nim powyższej redukcji/
Dowód powyższego twierdzenia, oczywiście, pozostawiamy jako ćwiczenie dla Czytelnika. Skorzystamy z niego podczas następującej redukcji naszego problemu.
Mamy dany graf  oraz liczbę
oraz liczbę 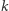 (rozmiar pokrycia, który sprawdzamy). Jeśli
(rozmiar pokrycia, który sprawdzamy). Jeśli 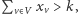 to zwracamy odpowiedź nie. W przeciwnym przypadku zmniejszamy nasz graf poprzez wyrzucenie z niego wierzchołków należących do
to zwracamy odpowiedź nie. W przeciwnym przypadku zmniejszamy nasz graf poprzez wyrzucenie z niego wierzchołków należących do 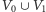 oraz zmniejszenie wielkości poszukiwanego pokrycia w reszcie grafu do
oraz zmniejszenie wielkości poszukiwanego pokrycia w reszcie grafu do 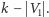 Odpowiada to zachłannemu wzięciu wszystkich wierzchołków z
Odpowiada to zachłannemu wzięciu wszystkich wierzchołków z 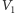 do naszego rozwiązania.
do naszego rozwiązania.
Pozostało wykazać, że redukcja ta jest bezpieczna oraz sprawdzić jakiej wielkości jest jądro po jej zastosowaniu. Dalej przez 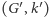 będę oznaczał instancję problemu, którą dostaniemy po zastosowaniu redukcji. Aby wykazać, że jest ona bezpieczna, wykażemy, że w
będę oznaczał instancję problemu, którą dostaniemy po zastosowaniu redukcji. Aby wykazać, że jest ona bezpieczna, wykażemy, że w 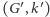 możemy znaleźć rozwiązanie wtedy i tylko wtedy, gdy mogliśmy je znaleźć w
możemy znaleźć rozwiązanie wtedy i tylko wtedy, gdy mogliśmy je znaleźć w 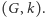
Zacznijmy od wykazania, że krok stwierdzający odpowiedź 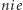 jest poprawny. Wiadomo, że wynik LP jest zawsze niewiększy niż ILP. Z tego też powodu, jeśli wynik LP będzie większy niż
jest poprawny. Wiadomo, że wynik LP jest zawsze niewiększy niż ILP. Z tego też powodu, jeśli wynik LP będzie większy niż 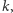 czyli stwierdzimy, że się nie da znaleźć rozwiązania w wersji bez warunku o całkowitości liczb, to tym bardziej z tym warunkiem by się nie dało.
czyli stwierdzimy, że się nie da znaleźć rozwiązania w wersji bez warunku o całkowitości liczb, to tym bardziej z tym warunkiem by się nie dało.
Druga część bezpieczeństwa nie jest wiele trudniejsza do wykazania. Najpierw uzasadnijmy implikację
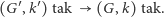
Jeśli 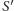 to pokrycie grafu
to pokrycie grafu  to na mocy wcześniejszej obserwacji, jeśli dołożymy wierzchołki z
to na mocy wcześniejszej obserwacji, jeśli dołożymy wierzchołki z 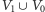 do grafu, a
do grafu, a 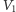 do pokrycia, to dostaniemy dokładnie pokrycie grafu
do pokrycia, to dostaniemy dokładnie pokrycie grafu 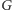 co najwyżej o rozmiarze
co najwyżej o rozmiarze 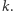
W przeciwną stronę: aby wykazać

korzystamy z twierdzenia Nemhausera-Trottera przytoczonego powyżej. Weźmiemy wtedy 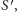 będące częścią wspólną pokrycia
będące częścią wspólną pokrycia 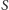 dla całego grafu, oraz
dla całego grafu, oraz 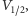 aby otrzymać pokrycie dla
aby otrzymać pokrycie dla 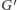 o rozmiarze co najwyżej
o rozmiarze co najwyżej 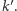
Ostatnią rzeczą jest wielkość jądra, które otrzymamy. Okazuje się, że rozmiar naszego nowego grafu 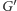 będzie wynosił co najwyżej
będzie wynosił co najwyżej 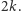 Wystarczy zauważyć, że jest on tym samym, co liczba wierzchołków "połowicznych", co z kolei wynosi nie więcej niż podwojona wielkość rozwiązania naszego LP, które musi być mniejsze niż
Wystarczy zauważyć, że jest on tym samym, co liczba wierzchołków "połowicznych", co z kolei wynosi nie więcej niż podwojona wielkość rozwiązania naszego LP, które musi być mniejsze niż 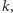 gdyż w przeciwnym przypadku dostalibyśmy już odpowiedź nie. Powyższe zdanie matematycznie zapiszemy w postaci
gdyż w przeciwnym przypadku dostalibyśmy już odpowiedź nie. Powyższe zdanie matematycznie zapiszemy w postaci
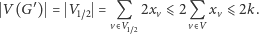
W ten oto prosty sposób udało nam się ograniczyć przestrzeń, którą musimy przejrzeć w czasie wykładniczym z  do
do  Nie jest to, oczywiście, jedyna redukcja, którą można zastosować do tego problemu. Okazuje się, że sam proces redukcji można jeszcze przyspieszyć, sprowadzając nasze LP do problemu przepływu w grafie. Po więcej szczegółów na temat algorytmów parametryzowanych (jak i tego sprowadzenia) można zajrzeć do książki Parameterized Algorithms, która na użytek własny jest dostępna za darmo w internecie.
Nie jest to, oczywiście, jedyna redukcja, którą można zastosować do tego problemu. Okazuje się, że sam proces redukcji można jeszcze przyspieszyć, sprowadzając nasze LP do problemu przepływu w grafie. Po więcej szczegółów na temat algorytmów parametryzowanych (jak i tego sprowadzenia) można zajrzeć do książki Parameterized Algorithms, która na użytek własny jest dostępna za darmo w internecie.
Oczywiście, nie jest to też jedyne zastosowanie programowania półcałkowitoliczbowego. W internecie można znaleźć pracę Half-integrality, LP-branching and FPT Algorithms, w której jest więcej szczegółów, jak i zastosowań tego rozwiązania. Serdecznie zachęcam do lektury!



 szaro z
szaro z  i czarno z
i czarno z 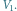 Na dole ten sam graf po wykonaniu na nim powyższej redukcji/
Na dole ten sam graf po wykonaniu na nim powyższej redukcji/