O modelach obliczeń komputerowych
Zastanówmy się nad następującym pytaniem: czym jest komputer? Sądzę, że odpowiedź na tak zadane pytanie może zależeć w znacznej mierze od tego, kogo o to pytamy. Taka sytuacja nie jest, oczywiście, czymś wyjątkowym. Jeśli zamiast informatyką zajmiemy się cukiernictwem i zapytamy: czym jest tort, to też różne osoby będą różnie odpowiadać...
Cukiernik opisujący tort widzi go jako kolejne poziome warstwy, które musi odpowiednio przygotować i w dobrej kolejności ułożyć. Łakomczuch - raczej widzi jego przekrój pionowy, stanowiący brzeg konkretnego kawałka. Jeśli zostaniemy przy gastronomii, ale przeskoczymy tym razem do piecyków kuchennych, znowu zaobserwujemy postulowaną dwoistość. Inżynier projektujący piecyk myśli o jego wydajności, o precyzji nastawienia temperatury, o tym, jak sprawić, żeby piecyk odpowiednio szybko się nagrzał itp., itd. Z kolei kucharz zakłada, że piecyk spełnia założenia podane w jego instrukcji i skupia się przede wszystkim na myśleniu, jak za jego pomocą wyczarować coś pysznego.
Spojrzenie na komputery jest w jakimś stopniu podobne do tego opisywanego wyżej. To znaczy mamy konstruktorów (fizyków, inżynierów), którzy chcą zbudować odpowiednio szybką i sprawną maszynę. Z drugiej strony, mamy użytkowników (informatyków, matematyków), którzy chcieliby z tego urządzenia po prostu korzystać. Te dwa spojrzenia mogą być bardzo różne, dlatego potrzebujemy czegoś, co jest odpowiednikiem instrukcji obsługi piecyka. To znaczy czegoś na tyle konkretnego, żeby konstruktorzy wiedzieli, co mają stworzyć, a z drugiej strony - na tyle abstrakcyjnego, żeby użytkownicy mogli z komputera korzystać, wcale nie znając szczegółów jego budowy. Tym czymś jest właśnie tytułowy formalny model obliczeń.
Zanim przejdziemy do opisów konkretnych modeli obliczeń - mała dygresja. Otóż przykład przejścia od świata fizyków i inżynierów do świata informatyków to szczególny przykład ogólniejszego zjawiska - tak zwanego abstrahowania. Pojęcie to ma, pozwolę sobie tutaj na arbitralne stwierdzenie, fundamentalne znaczenie w całej informatyce. Więcej - często występuje szeregowo, jako zbiór tak zwanych kolejnych warstw abstrakcji. Jest to z pewnością temat na cały oddzielny szczegółowy artykuł. Tym razem podam tylko ogólnikowy przykład: sieć Internet składa się z warstw abstrakcji: fizycznej, łącz danych, sieciowej, transportowej, sesji, prezentacji i aplikacji. Zawsze polega to na tym, że projektując pewną warstwę, zapominamy o szczegółach warstwy niższej, pozostawiając w naszej głowie tylko ogólną instrukcję jej obsługi. I dalej: efektem naszej pracy ma być nie tylko jakiś bardziej złożony produkt, ale również uproszczona instrukcja obsługi do niego. Czyli jak w życiu: równie ważne (a może i ważniejsze) od tego, z kim warto się znać i z kim się spotykać, jest to, kogo nie warto znać i gdzie nie bywać.
Po tym (przyznaję, przydługim) wstępie czas już przejść do konkretów. Zacznijmy więc od modelu obliczeń klasycznego komputera.
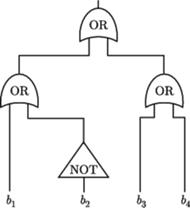
Obwód obliczający, czy liczba 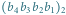 zapala zaznaczony segment na wyświetlaczu kalkulatora
zapala zaznaczony segment na wyświetlaczu kalkulatora
Dla programisty komputer to coś, co:
- ma pamięć, do której potrafimy wpisać jakieś dane;
- potrafi uruchomić zaprojektowany (w specjalnym języku) przez użytkownika program i jego wynik zapisać do pamięci;
- pozwala na odczytanie zawartości pamięci.
Oczywiście, modele takie jak wyżej mogą się istotnie różnić, zależnie od tego, jaki charakter ma pamięć (zwykle ciąg bitów ustalonej długości) oraz - przede wszystkim - jaki język opisu programu dopuszczamy. Przykładowe modele w tym duchu to: model maszyny Turinga, model maszyny RAM (random-access machine), interpreter języka Java czy model oparty o obwody logiczne złożone z bramek. Skupmy się na chwilę na tym ostatnim.

Model obwodów logicznych moglibyśmy opisać, na przykład, tak (modele tego typu są bardzo często stosowane do opisu układów scalonych):
- pamięć stanowią dwa wektory:
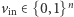 oraz
oraz 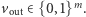 Użytkownik potrafi dowolnie ustalić wartość wektora
Użytkownik potrafi dowolnie ustalić wartość wektora 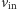 (czyli, żargonowo, "mamy
(czyli, żargonowo, "mamy 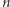 bitów wejściowych").
bitów wejściowych"). - Użytkownik może opisać dowolną sieć co najwyżej
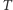 bramek OR, AND oraz NOT łączących wektor
bramek OR, AND oraz NOT łączących wektor 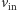 z wektorem
z wektorem 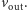 Wówczas komputer jest w stanie przypisać do wektora
Wówczas komputer jest w stanie przypisać do wektora 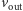 wynik obliczeń opisanej sieci na wektorze
wynik obliczeń opisanej sieci na wektorze 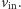
- Użytkownik po skończonym obliczeniu potrafi poznać wartość wektora
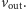
Przykład programu w tym modelu pokazuje rysunek obok.

Układ programowalny Altera Stratix IV GX FPGA realizujący model obliczeń oparty o obwody logiczne.
Poziom abstrakcji w tym przykładzie jest chyba dość jasny. Inżynier projektujący tak zdefiniowany komputer (Czytelnik Lubiący Konkrety może zapoznać się z technologią FPGA) ma na celu zastanowienie się, w jaki sposób stworzyć urządzenie, które:
- zawiera i potrafi (na żądanie użytkownika) ustawić dowolnie
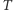 bramek logicznych;
bramek logicznych; - potrafi przyjąć podane przez użytkownika dane wejściowe (opis wektora
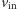 );
); - potrafi dokonać obliczenia i zwrócić użytkownikowi wynik obliczeń, czyli
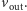
Powyższe zadanie zapewne jest bardzo trudne, wymaga znajomości fachowej wiedzy z elektroniki, wiedzy o działaniu tranzystorów itp., itd.
Z drugiej strony: informatyk, który z takiego urządzenia chce korzystać, może zupełnie nie znać fizyki i już myśleć tylko o algorytmice, czyli - w tym przypadku - nauce o takim przestawianiu klocków (bramek), żeby obliczało się dokładnie to, co chcemy i to możliwie szybko (a więc przy użyciu możliwie małej liczby bramek).
Przejdźmy teraz do tego, co stanowi esencję całego tego numeru Delty, czyli do komputerów kwantowych. Za chwilę przedstawimy formalny model obliczeń dla komputera kwantowego (czyli jego "instrukcję obsługi"). To, jakie problemy natury fizycznej napotykają projektanci takich potencjalnych komputerów, opisuje Rafał Demkowicz-Dobrzański. Z drugiej strony - jakie cuda potrafiłby zdziałać informatyk mający dostęp do takiego (hipotetycznego) urządzenia opisuje Wojciech Czerwiński, przybliżając szczegóły algorytmu Shora na rozkład dużych liczb na czynniki pierwsze. Prezentowany model korzysta z języka abstrakcyjnej algebry liniowej. Podstawy tej dziedziny prezentują Maciej Zdanowicz oraz Marek Kordos, przy okazji dowodząc, że programiści za kilkadziesiąt lat będą musieli znać chyba trochę więcej matematyki niż ci obecni. Na ile blisko (a na ile daleko) od stworzenia Prawdziwego Komputera Kwantowego jesteśmy w tej chwili pisze Piotr Zalewski. Dodatkowo kwartet Gardas, Jałowiecki, Dajka, Mierzejewski oraz (solo) Łukasz Rajkowski próbują przybliżyć Czytelnikowi, co już dziś jest komercyjnie dostępne. Po pierwsze omawiamy komputer D-Wave, który jednak realizuje (na 2048 kubitach) inny niż tu opisany model obliczeń kwantowych. Po drugie: omawiamy praktyczny protokół BB84, zakładający istnienie oraz możliwość szybkiego i taniego tworzenia "komputerów jednokubitowych" na żądanie.
Gorąco zachęcam do lektury tych i innych artykułów z tego numeru i bezzwłocznie przystępuję do prezentacji modelu obliczeń kwantowych.
- Do opisu stanu pamięci komputera kwantowego potrzebne są liczby zespolone, których zbiór oznaczamy symbolem
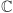 (więcej o nich pisze Marek Kordos na stronie 4). Zazwyczaj operować będziemy ciągami
(więcej o nich pisze Marek Kordos na stronie 4). Zazwyczaj operować będziemy ciągami 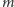 liczb zespolonych (tak zwanymi zespolonymi wektorami wymiaru
liczb zespolonych (tak zwanymi zespolonymi wektorami wymiaru 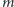 ), których zbiór oznaczamy
), których zbiór oznaczamy 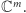 (Przykładowo:
(Przykładowo: 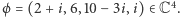 ) Dla wektorów określamy ich długość jako pierwiastek z sumy kwadratów modułów jego kolejnych współrzędnych. W naszym przykładzie długość
) Dla wektorów określamy ich długość jako pierwiastek z sumy kwadratów modułów jego kolejnych współrzędnych. W naszym przykładzie długość 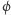 wynosi więc:
wynosi więc: 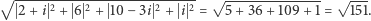
Opisem stanu pamięci komputera kwantowego jest jeden wektor o długości
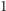 z przestrzeni
z przestrzeni 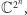 np.
np. 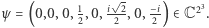 W świecie kwantowym często zapisujemy to samo w nieco innym (równoważnym) języku, mianowicie:
W świecie kwantowym często zapisujemy to samo w nieco innym (równoważnym) języku, mianowicie: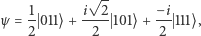
gdzie (jak łatwo się domyślić)
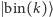 oznacza wektor złożony z
oznacza wektor złożony z 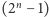 zer i jedynki na
zer i jedynki na 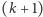 -szej współrzędnej, np.
-szej współrzędnej, np. 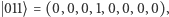 przy czym
przy czym 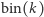 oznacza binarny zapis liczby
oznacza binarny zapis liczby 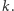
Wektory
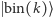 nazywamy wektorami bazy standardowej. Stany pamięci, które nie są takimi wektorami, a więc są sumą co najmniej dwóch różnych wektorów bazowych, fizycy lubią nazywać superpozycją. Jeśli stan pamięci jest opisany wektorem z
nazywamy wektorami bazy standardowej. Stany pamięci, które nie są takimi wektorami, a więc są sumą co najmniej dwóch różnych wektorów bazowych, fizycy lubią nazywać superpozycją. Jeśli stan pamięci jest opisany wektorem z 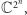 to mówimy, że nasz komputer operuje
to mówimy, że nasz komputer operuje 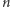 kubitami. Warto zwrócić uwagę, że stan pamięci klasycznego komputera operującego
kubitami. Warto zwrócić uwagę, że stan pamięci klasycznego komputera operującego  bitami opisujemy po prostu jednym ciągiem zer i jedynek długości
bitami opisujemy po prostu jednym ciągiem zer i jedynek długości  (np.
(np. 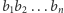 ), co możemy interpretować jako ustalenie jednego wektora bazy standardowej
), co możemy interpretować jako ustalenie jednego wektora bazy standardowej 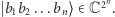 Przewaga komputera kwantowego polega zaś na tym, że w pamięci możemy trzymać bardziej wyrafinowane obiekty, a więc kombinacje liniowe takich wektorów (superpozycje), jak chociażby opisany wyżej wektor
Przewaga komputera kwantowego polega zaś na tym, że w pamięci możemy trzymać bardziej wyrafinowane obiekty, a więc kombinacje liniowe takich wektorów (superpozycje), jak chociażby opisany wyżej wektor 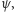 będący przykładem stanu pamięci komputera trójkubitowego.
będący przykładem stanu pamięci komputera trójkubitowego.
- Stan początkowy komputera użytkownik może ustalić zupełnie dowolnie, przy czym może używać iloczynu tensorowego do opisu (ta uwaga jest o tyle istotna, że cała przestrzeń ma wymiar wykładniczy, więc sam opis może czasem być ogromny; iloczyn tensorowy jest tu więc potencjalnym ułatwieniem). Iloczyn tensorowy
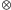 wektorów to bardzo prosta operacja, o której więcej piszemy na stronie 5. Na razie wystarczy nam tylko własność
wektorów to bardzo prosta operacja, o której więcej piszemy na stronie 5. Na razie wystarczy nam tylko własność 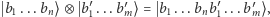 by zrozumieć, że ten sam wektor można opisać długo bądź zwięźle:
by zrozumieć, że ten sam wektor można opisać długo bądź zwięźle:
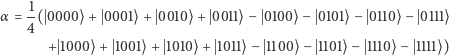
lub
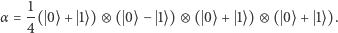
- Pojedyncze obliczenie na komputerze kwantowym odpowiada przemnożeniu stanu pamięci przez podaną przez użytkownika (nie byle jaką) macierz. W tym miejscu Czytelnik Algebraicznie Kulejący bardzo proszony jest o nieprzerażanie się tym pojęciem. Okazuje się, że nawet nie musimy dokładnie wiedzieć, jak się mnoży dowolną macierz przez wektor, bo wystarczą nam tylko trzy przykłady (dla macierzy H, T i CNOT oraz macierz identyczności I):
Jak widzimy macierze H i T dotyczą tylko wektorów jednokubitowych, a macierz CNOT - dwukubitowych. Aby opisać operację w wyższych wymiarach znów wolno nam się posłużyć iloczynem tensorowym, tym razem zastosowanym do macierzy. Ponownie jest to dość naturalna operacja (opisana szerzej późnej), a nam na razie wystarczy tylko własność
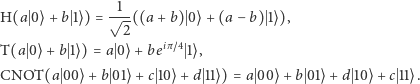
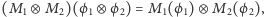 która jest prawdziwa, gdy wymiary się zgadzają. Intuicyjnie oznacza ona, że rozpatrywane macierze można przykładać lokalnie do dowolnie wybranych współrzędnych wielowymiarowego wektora stanu pamięci. Podajmy przykład, który powinien rozjaśnić tę operację:
Użytkownik może wybrać do opisu obliczenia dowolnie wybrany iloczyn tensorowy opisanych wyżej macierzy.
która jest prawdziwa, gdy wymiary się zgadzają. Intuicyjnie oznacza ona, że rozpatrywane macierze można przykładać lokalnie do dowolnie wybranych współrzędnych wielowymiarowego wektora stanu pamięci. Podajmy przykład, który powinien rozjaśnić tę operację:
Użytkownik może wybrać do opisu obliczenia dowolnie wybrany iloczyn tensorowy opisanych wyżej macierzy.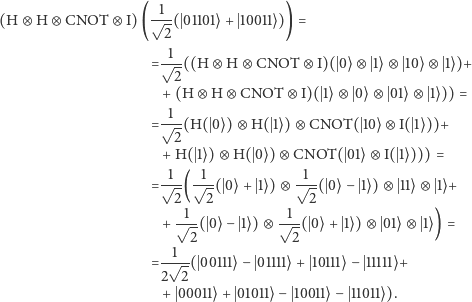
- Odczyt z pamięci jest w tym modelu bardzo nietrywialny. Przede wszystkim pomiar (zwykle) nie jest deterministyczny i może zwrócić różne wyniki dla tego samego stanu pamięci. Spróbujemy zaprezentować tutaj pewien uproszczony (ale wystarczający, by śledzić chociażby artykuł o faktoryzacji Shora) opis odczytu z komputera kwantowego. Użytkownik, chcąc dokonać pomiaru pamięci w pewnym
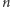 -kubitowym komputerze, musi podać pewien podzbiór indeksów
-kubitowym komputerze, musi podać pewien podzbiór indeksów 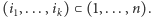 Jeśli teraz stan komputera to po prostu
Jeśli teraz stan komputera to po prostu 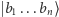 (czyli pewien wektor bazowy), to uzyskamy wynik
(czyli pewien wektor bazowy), to uzyskamy wynik 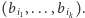 Jeśli natomiast stan komputera jest superpozycją
Jeśli natomiast stan komputera jest superpozycją 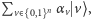 gdzie
gdzie 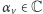 są współczynnikami przy wektorach bazowych
są współczynnikami przy wektorach bazowych 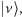 to pomiar jest istotnie niedeterministyczny. Uzyskamy wynik
to pomiar jest istotnie niedeterministyczny. Uzyskamy wynik 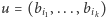 z prawdopodobieństwem
z prawdopodobieństwem 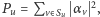 gdzie
gdzie 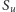 to zbiór tych wektorów
to zbiór tych wektorów 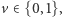 które na współrzędnych
które na współrzędnych 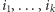 mają dokładnie wartości
mają dokładnie wartości 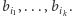
W komputerze kwantowym stan pamięci po pomiarze zmienia się (w świecie kwantowym pomiar musi zmienić stan pamięci!) na superpozycję tych składowych starego stanu, które są zgodne z pomiarem. Oczywiście niektóre stare składowe nie są zgodne z pomiarem, w związku z tym te, które są zgodne, muszą mieć zmienione współczynniki, aby długość całego wektora pamięci pozostała równa 1. Konkretnie rzecz biorąc, nowy stan pamięci po pomiarze to:
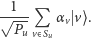
Zauważmy, że po pomiarze współrzędne
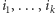 nie będą już nigdy istotne, bo są i tak zawsze takie same dla każdej składowej.
nie będą już nigdy istotne, bo są i tak zawsze takie same dla każdej składowej. - Użytkownik może wykonać dowolną sekwencję wielu obliczeń i odczytów (może je przeplatać).
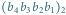 zapala zaznaczony segment na wyświetlaczu kalkulatora
zapala zaznaczony segment na wyświetlaczu kalkulatora![1 1 1 H = √--[ ] 2 1 − 1 T = [1 0 ] 0 eiπ~4 ⎡1 0 0 0⎤ ⎢⎢0 1 0 0⎥⎥ CNOT = ⎢⎢ ⎥⎥ ⎢⎢0 0 0 1⎥⎥ ⎢⎣0 0 1 0⎥⎦](/math/temat/informatyka/2017/11/19/O_modelach_obliczen_komputerowych/1x-f4dd8f5c6c2373e6f176e78e597c6681f948b5ef-dm-33,33,33-FF,FF,FF.gif)
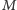 z przestrzeni
z przestrzeni 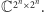 W wyniku obliczenia stan pamięci
W wyniku obliczenia stan pamięci 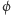 zmienia się na
zmienia się na 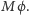 Użytkownik może podać dowolną macierz, co więcej, ma prawo używać iloczynu tensorowego do opisu (bezpośredni opis miałby rozmiar wykładniczy). Okazuje się, że (twierdzenie o uniwersalności) każdą macierz unitarną da się (z dowolnym przybliżeniem) uzyskać (korzystając z mnożenia i iloczynu tensorowego), mając do dyspozycji wyłącznie macierze H, T, CNOT i identyczność. Oczywiście, aby takie obliczenie było efektywne, ilość użytych macierzy podstawowych nie może być ogromna.
Użytkownik może podać dowolną macierz, co więcej, ma prawo używać iloczynu tensorowego do opisu (bezpośredni opis miałby rozmiar wykładniczy). Okazuje się, że (twierdzenie o uniwersalności) każdą macierz unitarną da się (z dowolnym przybliżeniem) uzyskać (korzystając z mnożenia i iloczynu tensorowego), mając do dyspozycji wyłącznie macierze H, T, CNOT i identyczność. Oczywiście, aby takie obliczenie było efektywne, ilość użytych macierzy podstawowych nie może być ogromna.