Pierwiastkowa dekompozycja zapytań
W niniejszym artykule chciałbym przedstawić Czytelnikom technikę, która może okazać się pomocna przy rozwiązywaniu różnych problemów informatycznych.

Rozważmy przykładowe zadanie. Dana jest 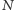 -elementowa tablica
-elementowa tablica 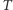 liczb naturalnych z przedziału
liczb naturalnych z przedziału 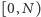 oraz
oraz 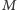 zapytań postaci
zapytań postaci 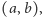 gdzie
gdzie 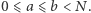 Dla każdego zapytania należy odpowiedzieć na pytanie ile różnych elementów ma podtablica
Dla każdego zapytania należy odpowiedzieć na pytanie ile różnych elementów ma podtablica ![|T[a..b].](/math/temat/informatyka/2017/02/28/Pierwiastkowa_dekompozycja_zapyt/7x-44010343e3e5642f9cc4dc8787085e77fb82cdf5-im-33,33,33-FF,FF,FF.gif) Można łatwo napisać algorytm, który dla zapytania znajduje odpowiedź w czasie
Można łatwo napisać algorytm, który dla zapytania znajduje odpowiedź w czasie 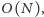 a więc dla
a więc dla 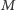 zapytań działa w czasie
zapytań działa w czasie 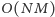 (kod źródłowy 1). Rozważmy jednak inne podejście do problemu. Zapamiętajmy wynik poprzedniego zapytania i spróbujmy zmodyfikować go tak, aby pasował do kolejnego (kod źródłowy 2).
(kod źródłowy 1). Rozważmy jednak inne podejście do problemu. Zapamiętajmy wynik poprzedniego zapytania i spróbujmy zmodyfikować go tak, aby pasował do kolejnego (kod źródłowy 2).
Nasz algorytm wciąż rozwiązuje problem w czasie 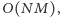 gdyż przejście z jednego zapytania do następnego może zająć
gdyż przejście z jednego zapytania do następnego może zająć 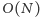 czasu. Jednak gdybyśmy zagwarantowali, że kolejne zapytania będą podobne, algorytm mógłby działać szybciej. Rozważmy problem, w którym znamy na wstępie wszystkie zapytania. Możemy wybrać kolejność w jakiej będziemy na nie odpowiadać. Załóżmy dla uproszczenia, że
czasu. Jednak gdybyśmy zagwarantowali, że kolejne zapytania będą podobne, algorytm mógłby działać szybciej. Rozważmy problem, w którym znamy na wstępie wszystkie zapytania. Możemy wybrać kolejność w jakiej będziemy na nie odpowiadać. Załóżmy dla uproszczenia, że 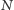 jest kwadratem liczby naturalnej. Okazuje się, że istnieje kolejność, która gwarantuje, że nasz algorytm wykona jedynie
jest kwadratem liczby naturalnej. Okazuje się, że istnieje kolejność, która gwarantuje, że nasz algorytm wykona jedynie 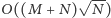 operacji.
operacji.
Podzielmy przedział 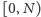 na
na 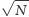 części:
części:

Każdy z tych przedziałów jest rozmiaru 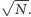 Teraz utwórzmy kubełek dla każdego z nich. Dla każdego zapytania
Teraz utwórzmy kubełek dla każdego z nich. Dla każdego zapytania 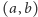 patrzymy do którego z tych kubełków wpada
patrzymy do którego z tych kubełków wpada 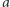 i umieszczamy to zapytanie w odpowiednim kubełku. Następnie w każdym kubełku sortujemy zapytania rosnąco po wartościach
i umieszczamy to zapytanie w odpowiednim kubełku. Następnie w każdym kubełku sortujemy zapytania rosnąco po wartościach 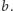 Przeglądamy teraz kubełki po kolei i odpowiadamy na zapytania zgodnie z ustalonym porządkiem.
Przeglądamy teraz kubełki po kolei i odpowiadamy na zapytania zgodnie z ustalonym porządkiem.

Obliczmy złożoność naszego algorytmu. Rozważmy dwie sytuacje. W pierwszej z nich oba zapytania należą do tego samego kubełka. W takiej sytuacji stare_a oraz a należą do tego samego przedziału. Nie wykonamy zatem więcej niż 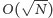 operacji dodaj i usuń w trakcie zmiany stare_a na a. Jeśli chodzi o wartości stare_b oraz b to są one w ramach jednego kubełka posortowane rosnąco. Oznacza to, że jeśli dwa zapytania są w jednym kubełku, to będziemy wykonywać jedynie operację dodaj. A więc dla ustalonego kubełka sumarycznie wystarczy wykonać jedynie
operacji dodaj i usuń w trakcie zmiany stare_a na a. Jeśli chodzi o wartości stare_b oraz b to są one w ramach jednego kubełka posortowane rosnąco. Oznacza to, że jeśli dwa zapytania są w jednym kubełku, to będziemy wykonywać jedynie operację dodaj. A więc dla ustalonego kubełka sumarycznie wystarczy wykonać jedynie 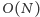 takich operacji przy zmianach stare_b na b. Rozważmy teraz sytuację w której zapytania należą do różnych kubełków. Jak powiedzieliśmy wcześniej, w najgorszym przypadku wykonamy
takich operacji przy zmianach stare_b na b. Rozważmy teraz sytuację w której zapytania należą do różnych kubełków. Jak powiedzieliśmy wcześniej, w najgorszym przypadku wykonamy 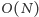 operacji między dwoma zapytaniami. Jednak taka sytuacja zdarzy się co najwyżej
operacji między dwoma zapytaniami. Jednak taka sytuacja zdarzy się co najwyżej 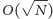 razy, bo tylko tyle mamy kubełków. A więc sumarycznie nasz algorytm zadziała w czasie
razy, bo tylko tyle mamy kubełków. A więc sumarycznie nasz algorytm zadziała w czasie

A teraz dwa ćwiczenia dla Drogiego Czytelnika. Pierwsze jest następujące: mając daną tablicę ![| −1] T [0..N](/math/temat/informatyka/2017/02/28/Pierwiastkowa_dekompozycja_zapyt/6x-bc7be24138d98d6981797b512b0a2527f4bc7cfd-im-33,33,33-FF,FF,FF.gif) oraz
oraz 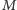 zapytań
zapytań 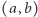 należy dla każdego zapytania odpowiedzieć ile inwersji znajduje się w podtablicy
należy dla każdego zapytania odpowiedzieć ile inwersji znajduje się w podtablicy ![|T[a..b].](/math/temat/informatyka/2017/02/28/Pierwiastkowa_dekompozycja_zapyt/9x-bc7be24138d98d6981797b512b0a2527f4bc7cfd-im-33,33,33-FF,FF,FF.gif) Inwersją w tablicy
Inwersją w tablicy 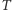 nazywamy taką parę liczb
nazywamy taką parę liczb  że
że 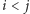 oraz
oraz ![|T[i] > T [ j].](/math/temat/informatyka/2017/02/28/Pierwiastkowa_dekompozycja_zapyt/13x-bc7be24138d98d6981797b512b0a2527f4bc7cfd-im-33,33,33-FF,FF,FF.gif) Drugie zaś brzmi: mając dany graf
Drugie zaś brzmi: mając dany graf 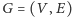 oraz tablicę jego krawędzi
oraz tablicę jego krawędzi 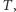 należy dla każdego zapytania
należy dla każdego zapytania 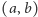 odpowiedzieć na pytanie ile spójnych składowych ma graf obcięty do krawędzi
odpowiedzieć na pytanie ile spójnych składowych ma graf obcięty do krawędzi ![T [a..b].](/math/temat/informatyka/2017/02/28/Pierwiastkowa_dekompozycja_zapyt/17x-bc7be24138d98d6981797b512b0a2527f4bc7cfd-im-33,33,33-FF,FF,FF.gif) Każde z tych zadań można rozwiązać za pomocą opisanej w artykule techniki, nazywanej pierwiastkową dekompozycją zapytań, jednakże wymagają one dodatkowego pomysłu. Mam nadzieję, że rozwiązywanie tych zadań przyniesie Czytelnikom dużo frajdy.
Każde z tych zadań można rozwiązać za pomocą opisanej w artykule techniki, nazywanej pierwiastkową dekompozycją zapytań, jednakże wymagają one dodatkowego pomysłu. Mam nadzieję, że rozwiązywanie tych zadań przyniesie Czytelnikom dużo frajdy.