W nauce, szczególnie w matematyce i informatyce, jest wiele rodzajów złożoności:

• złożoność obliczeniowa (czasowa lub pamięciowa) algorytmów: ilość zasobów (czasu, pamięci) potrzebnych do algorytmicznego rozwiązania danego problemu, w zależności od rozmiaru danych wejściowych,
• złożoność informacyjna Kołmogorowa: długość najkrótszego programu generującego dane słowo,
• złożoność cyklomatyczna: stopień skomplikowania programu komputerowego, liczba możliwych ścieżek wykonania kodu źródłowego.

Czy istnieją definicje i miary złożoności na tyle ogólne, aby dla wszystkich rzeczywistych lub abstrakcyjnych bytów jednoznacznie ocenić, czy coś jest złożone, czy nie? Wydaje się, że jest zbyt dużo skomplikowanych struktur, które mają ze sobą niewiele wspólnego, aby takie uniwersalne definicje i miary miały sens. Okazuje się, że istnieje dziedzina nauki o nazwie złożone systemy (ang. complex systems), zajmująca się badaniem właśnie takich pozornie zupełnie różnych struktur, mających jednak specyficzne cechy powodujące, że struktury te i procesy z nimi związane określa się jako złożone. Z uwagi na różnorodność badanych systemów trudno nawet zdefiniować tę dziedzinę i systemy będące przedmiotem jej badań. W wielu pracach naukowych przyjmuje się dość ogólną definicję:

Przedstawiona definicja jest (celowo) nieprecyzyjna, nie mówi, jak dużo ma być komponentów systemu, czym są emergentne własności i interakcja. Istnieją mniej lub bardziej ogólne wersje tej definicji oraz zupełnie odmienne (czasem zamiast ścisłej definicji podaje się przykłady systemów uważanych za złożone oraz ich wspólne cechy powodujące tę złożoność). W większości definicji występują takie pojęcia jak: wiele komponentów, interakcja, emergencja. Pod tym ostatnim pojęciem kryje się istota złożonych systemów, emergencja oznacza, że "całość to więcej niż suma części". Dla matematyków może być to zaskakujące, przecież 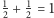! Więc jak to możliwe? Komponenty złożonych systemów są dużo prostsze niż całe systemy, to samo dotyczy ich pojedynczych interakcji - zazwyczaj nie są one skomplikowane. To kolektywna interakcja wielu prostszych elementów powoduje, że cały system jest bardziej skomplikowany niż elementy składowe, czy nawet ich suma, ale bez interakcji. Przyjrzyjmy się przykładom złożonych systemów.

Społeczeństwo - grupa ludzi, których interakcja może prowadzić do wybuchu wojen, epidemii, powstawania nowych pomysłów, czy budowy skomplikowanych urządzeń (które też mogą być złożone, np. komputery, samochody i samoloty składają się z wielu prostszych części, które same nie są w stanie wiele zrobić, a złożone w odpowiednie konfiguracje potrafią kolektywnie sprawić, że samoloty latają, samochody jeżdżą, a komputery wykonują skomplikowane obliczenia). Czasem jeden człowiek sam nie potrafi rozwiązać pewnego bardzo trudnego problemu, np. matematycznego. Grupa 100 świetnych matematyków również może sobie nie poradzić, jeżeli będą oni pracować osobno, nawet gdy zsumujemy wyniki samodzielnej pracy każdego z nich, to i tak nie znajdziemy w nich rozwiązania. Jednak kiedy zaczną oni współpracować, wymieniać się pomysłami (czyli będą w interakcji), to ich wiedza może się świetnie uzupełniać, wyniki jednej osoby mogą zainspirować pozostałych, pokonanie jednej z przeszkód spowoduje, że kolejna osoba będzie mogła wykorzystać swoją wiedzę, aby wykonać kolejny krok na drodze do rozwiązania problemu. W taki sposób funkcjonuje nauka i (emergentnie) pojawia się postęp techniczny.

Inne przykłady emergentnych zjawisk w społeczeństwie dotyczą giełdy i rynków finansowych: interakcja wielu użytkowników poprzez handel produktami może prowadzić do powstawania bańki spekulacyjnej, kryzysu finansowego. Sytuacja na giełdzie zależy od wielu czynników zewnętrznych, np. sytuacji gospodarczej. Jest to przykład ważnej cechy wielu złożonych systemów - są one otwarte, może na nie wpływać otoczenie, a one mogą się adaptować do jego warunków. Systemy mające tę cechę określa się mianem złożone systemy adaptacyjne.

Kolejnym przykładem jest ruch drogowy: interakcja ludzi i używanych przez nich pojazdów może prowadzić do wypadków i zatorów. Ciekawe jest to, że zatory w ruchu drogowym można rozładowywać oraz im przeciwdziałać za pomocą innego złożonego systemu: systemu zarządzania ruchem, w którym programy sterujące sygnalizacją świetlną na skrzyżowaniach mogą ze sobą współpracować (np. wymieniać informacje o natężeniu ruchu), aby nie dopuścić do powstania zatoru.

Sam człowiek, element składowy społeczeństwa, też jest złożonym systemem: jego organizm składa się z wielu narządów, które muszą współpracować, aby podtrzymywać życie, a narządy zbudowane są z komórek, które również są w interakcji. Dalej: komórki zbudowane są z substancji chemicznych, które powstają poprzez reakcję (interakcję) jeszcze prostszych substancji. Przykład ten ilustruje następną cechę złożonych systemów - hierarchiczność (w tym przypadku: od substancji chemicznych i komórek do człowieka i społeczeństwa).

Skąd u człowieka biorą się tak złożone cechy jak inteligencja, świadomość i emocje? Przypuszcza się, że wynikają one z prostych interakcji neuronów w mózgu. A genom ludzki? Poprzez interakcje w sieciach regulatorowych kontrolowana jest ekspresja genów, co decyduje o budowie i złożoności ludzkiego organizmu.

Złożone systemy nie dotyczą jedynie ludzi, występują też w świecie zwierząt i roślin. Proste interakcje między zwierzętami powodują, że podróżują one w zorganizowanych strukturach, takich jak ławice ryb, klucze ptaków, a kolonia mrówek może wybudować mrowisko i dostarczać do niego pożywienie. Na przykładzie ludzi i zwierząt widać, że z interakcją związane jest przekazywanie i przetwarzanie informacji (np. mowa, feromony, informacja wizualna), co jest kolejną wspólną cechą wielu złożonych systemów.

Złożone systemy nie dotyczą też jedynie istot żywych (choć często sprawiają wrażenie, że są "żywe"), np. interakcja poprzez siły grawitacji może formować tak skomplikowane struktury, jak Układ Słoneczny. Problem wyznaczenia toru ruchu ciał oddziałujących zgodnie z prawami grawitacji Newtona trudno rozwiązać analitycznie z uwagi na nieliniowość interakcji (nie da się ich opisać za pomocą układu równań liniowych), a także numerycznie - z uwagi na wrażliwość na warunki początkowe (niewielka zmiana parametrów układu, jego komponentów lub interakcji może powodować całkowicie inną jego ewolucję). Zarówno nieliniowość, jak i wrażliwość na warunki początkowe to typowe własności złożonych systemów.

Złożone systemy nie dotyczą też jedynie bytów fizycznych. Przykładem abstrakcyjnego złożonego systemu, który ma wiele zastosowań praktycznych, są automaty komórkowe. Zostały one odkryte przez Stanisława Ulama i Johna von Neumanna w Los Alamos w latach 40. XX wieku, a potem spopularyzowane m.in. poprzez Grę w życie Johna Conwaya. Składają się ze zbioru komórek rozmieszczonych na regularnej siatce (np. na płaszczyźnie), które w każdej chwili mają określony stan pochodzący ze skończonego zbioru możliwych stanów. Ewolucja automatu odbywa się w dyskretnych krokach, w każdym kroku stan danej komórki zależy od stanów pewnego podzbioru komórek (komórki są więc w interakcji). W definicjach automatów komórkowych ten podzbiór zazwyczaj pochodzi z otoczenia komórki, a reguły przejścia pomiędzy stanami są deterministyczne i takie same dla wszystkich komórek. Są jednak wyjątki, np. model Nagela-Schreckenberga (model Na-Sch), którego opis pojawi się w dalszej części artykułu.

Z uwagi na interakcje często trudno jest dokładnie przewidzieć ewolucję automatu komórkowego bez jej obserwacji, np. poprzez uruchomienie symulacji komputerowej. Cechę tę, znaną jako obliczeniowa nieredukowalność, wprowadził w książce A New Kind of Science Stephen Wolfram. Jest to kolejna wspólna cecha wielu złożonych systemów. Inną własnością, widoczną świetnie na przykładzie automatów komórkowych, jest współistnienie cech (samo)organizacji i dezorganizacji (chaosu). Choć ewolucja systemu może wyglądać na chaotyczną, można w niej odnaleźć uporządkowane wzorce, dające wrażenie, że system jest w pewien sposób zorganizowany pomimo nieskoordynowanych interakcji i braku centralnego sterowania. Złożone systemy są więc czymś pomiędzy układami prostymi, w których wszystko można szybko i precyzyjnie obliczyć, a układami losowymi, dla których można prowadzić głównie rozważania statystyczne.

Jak widać, złożone systemy występują w wielu obszarach, od skali mikro do makro. Jest to intrygujące, gdyż niewiele jest w nauce przypadków tak dużej uniwersalności pojęć i praw! Fascynujące jest też to, że wiele złożonych systemów ma znacznie więcej wspólnych cech, niż sugeruje to ich definicja, a przez to w badaniach dotyczących pewnych złożonych systemów czasami korzysta się z innych!

Przykładem może być wspomniany już ruch drogowy, którego modelowaniem zajmuje się naukowo autor niniejszego artykułu. W zjawisku tym wielu agentów (kierowcy, a w przyszłości - pojazdy autonomiczne) stara się osiągnąć cel, którym zazwyczaj jest szybkie dotarcie do punktu docelowego, korzystając z dostępnej infrastruktury drogowej i przestrzegając przepisów. Agenci współdzielą infrastrukturę, więc są w interakcji ze sobą i z otoczeniem, np. dostosowują prędkość do warunków jazdy, wyprzedzają inne pojazdy. Te interakcje mogą powodować emergentne zjawiska: wypadki, powstawanie zatorów. W przyszłości, gdy powszechna będzie komunikacja pomiędzy pojazdami autonomicznymi (komunikacja V2V - vehicle-to-vehicle) oraz pojazdami i infrastrukturą (V2I - vehicle-to-infrastructure), możliwych interakcji będzie więcej, np. synchronizowanie manewrów, informowanie o zamiarze wyprzedzania, zbliżaniu się do skrzyżowania. Emergentnych sytuacji będzie też więcej (i będą zależeć od algorytmów jazdy zaimplementowanych w komputerach pokładowych pojazdów), np. wspólna jazda w stabilnym układzie, podobnie do lotu klucza ptaków lub ruchu ławicy ryb.

Ruch drogowy może być modelowany matematycznie za pomocą innego złożonego systemu i to relatywnie bardzo prostego: automatu komórkowego! Przykładem może być wspomniany już model Na-Sch, w którym automat komórkowy reprezentowany jest jako jednowymiarowa, cykliczna taśma podzielona na komórki. Czas jest dyskretny, w każdym kroku komórki mogą być puste (stan null) lub zajęte przez 1 pojazd (stan to prędkość pojazdu). Pojazdy poruszają się w jednym kierunku (gdy dotrą do końca taśmy, pojawiają się na jej początku) z dyskretnymi prędkościami odpowiadającymi liczbie komórek, o które pojazd się przemieścił.

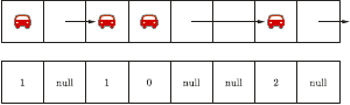
Automat komórkowy ilustrujący model Na-Sch - stan komórek to prędkość, z jaką pojazd się przemieścił

Położenia i prędkości pojazdów w każdym kroku obliczane są zgodnie z czteroetapową regułą ruchu. Najpierw każdy pojazd stara się przyspieszyć o 1 jednostkę, ale tak, aby nie przekroczyć maksymalnej dopuszczalnej prędkości (w oryginalnym modelu Na-Sch było to 5 komórek). Drugi etap to warunek bezpieczeństwa: prędkość jest redukowana tak, aby na pewno nie wjechać w inny pojazd. Trzeci etap wprowadza niedeterminizm: z pewnym prawdopodobieństwem prędkość obliczona w pierwszych dwóch krokach jest redukowana o 1 jednostkę. W czwartym etapie pojazd przemieszcza się do przodu o liczbę komórek odpowiadającą obliczonej prędkości.

Model Na-Sch stał się bardzo popularny i doczekał się wielu rozszerzeń (np. wiele pasów ruchu, model dwuwymiarowy, graf skierowany), gdyż pomimo swojej prostoty modeluje bardzo złożony ruch drogowy z dużą zgodnością z rzeczywistością oraz wyjaśnia ważne zjawiska, np. spontaniczne formowanie się korków. Pokazuje to uniwersalność złożonych systemów i olbrzymie możliwości w nich ukryte.