Co to jest?

Losowość w komputerze

Od komputera oczekujemy przede wszystkim precyzji i dokładności. Program szukający wzorca w edytowanym tekście czy arkusz kalkulacyjny podsumowujący nasze miesięczne wydatki ma po prostu dać poprawny wynik. Wszelkie przejawy niedeterminizmu, losowości czy jakiejś niestabilności przywołują skojarzenia z działaniem niepożądanym. Zwykle to prawda: dobry program ma obliczyć, narysować czy wyanimować dokładnie to, czego od niego chcemy. Okazuje się jednak, że czasem losowość jest nie tylko wskazana, ale wręcz niezbędna.

Losowości potrzebuje komputer chociażby wtedy, gdy użytkownik ma ochotę na pogranie w niektóre gry (jak kultowy Saper czy aktualnie będący na topie 2048). Także niektóre procesy fizyczne najlepiej modeluje się na komputerze tak zwaną metodą Monte Carlo, która jest przecież silnie niedeterministyczna. Losowość jest również niezbędna w kryptologii.

No dobrze, ale skąd komputer bierze - jak już wiemy, niezbędne mu - losowe bity?

Sprawa wcale nie jest tak banalna, jak by się mogło wydawać. Przecież w komputerze nie ma ukrytej monety, którą mógłby on w razie potrzeby podrzucać. Więcej: cała jego konstrukcja jest tak pomyślana, żeby jego zachowanie było w pełni przewidywalne (bo opisane przez wykonywane programy). Na losowość w komputerze trzeba więc patrzeć tak, jak na swoisty zasób, który komputer musi jakoś pozyskać. I pozyskuje, mierząc czy analizując wszystko co wokół, a co nie jest w pełni deterministyczne. Trzecia cyfra po przecinku pomiaru temperatury procesora (w komputerze jest termometr!) czy krzywizna ruchu myszki, którą operuje użytkownik, to przykłady zjawisk, które komputer ma w zasięgu cyfrowego wzroku. Są to z pewnością zjawiska w jakiejś mierze losowe, ale z pewnością nie jednostajnie losowe, a takie będą dla nas najcenniejsze.

Na szczęście nie wszystko stracone. Istnieją metody pozwalające (w deterministyczny sposób!) z losowości słabej wyprodukować losowość niemal jednostajną! Podamy prosty przykład: załóżmy, że mamy niesymetryczną monetę (orzeł trafia się z szansą 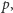$p,$ a reszka 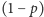$(1− p)$ ). Potrzebujemy jednego prawdziwie losowego bitu. Rzućmy monetą dwukrotnie. I tak: jeśli wypadły dwa orły albo dwie reszki, to próbę uznajemy za spaloną i eksperyment powtarzamy. Umówmy się teraz, że wynik OR interpretujemy jako orła, a RO - jako reszkę. Jaka jest szansa na ciąg OR? Oczywiście 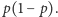$|p(1− p).$ A na ciąg RO? Widać, że 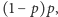$(1− p)p,$ czyli dokładnie tyle samo! A więc ani "nowy orzeł", ani "nowa reszka" nie mają żadnej przewagi.

Wszystko jest dokładnie symetryczne, a więc możemy w ten sposób produkować naprawdę losowe bity.

Metody takie jak wyżej nazywamy w informatyce ekstraktorami losowości. Dobry ekstraktor to taki, który po prostu produkuje coś bardzo losowego z czegoś słabo losowego. W tym miejscu należałoby dokładnie zdefiniować, co rozumiemy pod tymi terminami.

Kluczowym pojęciem, które posłuży jako "miara losowości" jest tutaj tak zwana min-entropia rozkładu prawdopodobieństwa. Dla rozkładu skończonego określamy

)=minx>X(−log(P(X=x))). H

Łatwo sprawdzić, że jeśli dopuszczamy 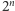$2n$ różnych wartości pomiaru, to rozkład jednostajny ma min-entropię równą 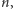$n,$ a rozkład skupiony w jednym punkcie ma min-entropię zero. Dobry ekstraktor to taki, który ze źródła (albo kilku niezależnych źródeł) o słabej min-entropii (czyli gdy stosunek min-entropii do logarytmu z mocy nośnika jest mały) generuje rozkład bliski jednostajnemu (sama min-entropia przy deterministycznym przekształceniu wzrosnąć nie może, ale już opisany stosunek tak, o ile tylko przeciwdziedzina jest istotnie mniejsza niż dziedzina).

Badania nad ekstraktorami to poważna i ciekawa dziedzina twardej matematyki. Do niedawna problemem otwartym było podanie przykładu ekstraktora dwuźródłowego, który oblicza choć jeden niemal losowy bit, przy założeniu, że oba niezależne źródła mają min-entropię poniżej połowy maksymalnie możliwej (a więc mniejszej niż 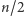$n/2$ ).

Pierwszy taki przykład podał w roku 2005 laureat medalu Fieldsa, Jean Bourgain. W roku bieżącym wynik ten poprawili spektakularnie Eshan Chattopadhyay oraz David Zuckerman, podając konstrukcję, która działa dla dwóch niezależnych źródeł o min-entropii co najmniej 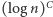$(logn)C$ dla pewnej (dużej) stałej 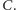$C.$ Ich praca Explicit Two-Source Extractors and Resilient Functions była prezentowana w czerwcu na konferencji STOC 2016 (48th Annual Symposium on Theory of Computing) w Massachusetts Institute of Technology i została wyróżniona jedną z trzech równorzędnych nagród przyznawanych za najlepsze prace.