Informatyczny kącik olimpijski
Kuglarz
W tym miesiącu omówimy zadanie Kuglarz z pierwszej rundy Potyczek Algorytmicznych 2014. Tytułowy kuglarz zaprasza przechodniów do następującej gry...
Zadanie 1. Na stoliku w rzędzie ustawił 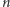 kubków z numerami
kubków z numerami 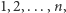 a zawczasu pod niektórymi schował kauczukowe kulki. Jeśli grający dokładnie odgadnie, które to kubki, to dostaje nagrodę. Kuglarz odpłatnie udziela grającemu podpowiedzi. Za
a zawczasu pod niektórymi schował kauczukowe kulki. Jeśli grający dokładnie odgadnie, które to kubki, to dostaje nagrodę. Kuglarz odpłatnie udziela grającemu podpowiedzi. Za 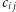 bajtogroszy (dla
bajtogroszy (dla 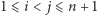 ) gotów jest zdradzić, jaka jest parzystość liczby kulek schowanych pod kubkami o kolejnych numerach
) gotów jest zdradzić, jaka jest parzystość liczby kulek schowanych pod kubkami o kolejnych numerach 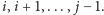 Znając ceny wszystkich możliwych podpowiedzi, należy wyznaczyć koszt zebrania informacji, które pozwolą określić z całą pewnością, pod którymi kubkami znajdują się kulki. Ściślej rzecz biorąc, należy znaleźć najmniejszą taką liczbę
Znając ceny wszystkich możliwych podpowiedzi, należy wyznaczyć koszt zebrania informacji, które pozwolą określić z całą pewnością, pod którymi kubkami znajdują się kulki. Ściślej rzecz biorąc, należy znaleźć najmniejszą taką liczbę 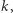 że istnieje strategia zadawania pytań, która niezależnie od odpowiedzi kuglarza pozwala na zlokalizowanie kulek za co najwyżej
że istnieje strategia zadawania pytań, która niezależnie od odpowiedzi kuglarza pozwala na zlokalizowanie kulek za co najwyżej 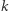 bajtogroszy.
bajtogroszy.
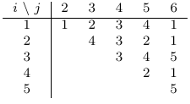
Rys. 1 Przykładowa tabela kosztów dla 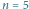 kubków. Koszt
kubków. Koszt 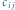 pytania
pytania 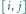 znajduje się na przecięciu wiersza
znajduje się na przecięciu wiersza 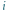 z kolumną
z kolumną 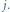

Spróbujmy wyznaczyć rozwiązanie dla tabelki kosztów z rysunku 1. Naiwne zadanie pytań o jednokubkowe przedziały kosztowałoby 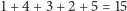 bajtogroszy. Czy da się lepiej? Oznaczmy przez
bajtogroszy. Czy da się lepiej? Oznaczmy przez ![|[i, j]](/math/temat/informatyka/2015/04/19/Kuglarz/2x-17ad7e88a54f9f0a1eb440b32c7f5177ce445291-im-33,33,33-FF,FF,FF.gif) podpowiedź na temat parzystości liczby kulek pod kubkami o numerach
podpowiedź na temat parzystości liczby kulek pod kubkami o numerach 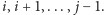 Zacznijmy od pytań o małych kosztach: pytanie
Zacznijmy od pytań o małych kosztach: pytanie ![|[1,2]](/math/temat/informatyka/2015/04/19/Kuglarz/4x-17ad7e88a54f9f0a1eb440b32c7f5177ce445291-im-33,33,33-FF,FF,FF.gif) daje nam informację, czy pod pierwszym kubkiem znajduje się kulka, a pytanie
daje nam informację, czy pod pierwszym kubkiem znajduje się kulka, a pytanie ![[1,6]](/math/temat/informatyka/2015/04/19/Kuglarz/5x-17ad7e88a54f9f0a1eb440b32c7f5177ce445291-im-33,33,33-FF,FF,FF.gif) o parzystość liczby wszystkich kulek. Zadanie ich kosztuje
o parzystość liczby wszystkich kulek. Zadanie ich kosztuje 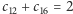 bajtogrosze. Następne pytanie o małym koszcie to
bajtogrosze. Następne pytanie o małym koszcie to ![| [2,6],](/math/temat/informatyka/2015/04/19/Kuglarz/7x-17ad7e88a54f9f0a1eb440b32c7f5177ce445291-im-33,33,33-FF,FF,FF.gif) ale czy rzeczywiście opłaca się je zadawać? Nie, gdyż na podstawie poprzednich podpowiedzi, znamy parzystość kulek na pozycjach od 2 do 5.
ale czy rzeczywiście opłaca się je zadawać? Nie, gdyż na podstawie poprzednich podpowiedzi, znamy parzystość kulek na pozycjach od 2 do 5.
Tę obserwację można nieco uogólnić: na podstawie odpowiedzi na dwa dowolne pytania z trójki ![[i, j],[ j,k]](/math/temat/informatyka/2015/04/19/Kuglarz/1x-d59ff70ca6e7a4815f0b4340e6a32c6a95d0c9af-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![[i,k]](/math/temat/informatyka/2015/04/19/Kuglarz/2x-d59ff70ca6e7a4815f0b4340e6a32c6a95d0c9af-im-33,33,33-FF,FF,FF.gif) jesteśmy w stanie wyznaczyć odpowiedź na trzecie z tych pytań. Tutaj następuje kluczowy pomysł: zbudujmy graf pusty
jesteśmy w stanie wyznaczyć odpowiedź na trzecie z tych pytań. Tutaj następuje kluczowy pomysł: zbudujmy graf pusty 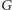 o
o 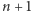 wierzchołkach
wierzchołkach 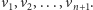 Dla każdego zadanego przez nas pytania
Dla każdego zadanego przez nas pytania ![[i, j],](/math/temat/informatyka/2015/04/19/Kuglarz/6x-d59ff70ca6e7a4815f0b4340e6a32c6a95d0c9af-im-33,33,33-FF,FF,FF.gif) będziemy w tym grafie łączyć krawędzią wierzchołki
będziemy w tym grafie łączyć krawędzią wierzchołki 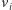 oraz
oraz 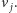 Zachodzi teraz następujący fakt: jeśli wierzchołki
Zachodzi teraz następujący fakt: jeśli wierzchołki 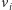 oraz
oraz 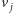 należą do tej samej spójnej składowej grafu, to albo zadaliśmy już kiedyś pytanie
należą do tej samej spójnej składowej grafu, to albo zadaliśmy już kiedyś pytanie ![| [i, j],](/math/temat/informatyka/2015/04/19/Kuglarz/11x-d59ff70ca6e7a4815f0b4340e6a32c6a95d0c9af-im-33,33,33-FF,FF,FF.gif) albo jesteśmy w stanie wyznaczyć na nie odpowiedź na podstawie dotychczasowych podpowiedzi kuglarza. Istotnie: jeśli wierzchołki te łączy ścieżka
albo jesteśmy w stanie wyznaczyć na nie odpowiedź na podstawie dotychczasowych podpowiedzi kuglarza. Istotnie: jeśli wierzchołki te łączy ścieżka 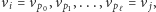 to przez indukcję można pokazać, że możemy wyznaczyć odpowiedzi na kolejne pytania
to przez indukcję można pokazać, że możemy wyznaczyć odpowiedzi na kolejne pytania ![| [p0,p1],[p0, p2],...,[p0,p ℓ].](/math/temat/informatyka/2015/04/19/Kuglarz/13x-d59ff70ca6e7a4815f0b4340e6a32c6a95d0c9af-im-33,33,33-FF,FF,FF.gif)
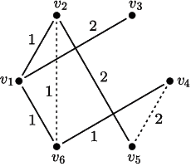
Rys. 2 Graf  po rozważeniu podpowiedzi o kosztach 1 i 2. Zadajemy pytania odpowiadające pogrubionym krawędziom.
po rozważeniu podpowiedzi o kosztach 1 i 2. Zadajemy pytania odpowiadające pogrubionym krawędziom.
Z powyższych rozważań wynikają następujące wnioski. Nie opłaca się prosić o podpowiedzi, które spowodują powstanie cyklu w grafie, zatem po zadaniu dokładnie  pytań graf
pytań graf  który nam powstanie, będzie drzewem, a zdobyte informacje umożliwią zlokalizowanie wszystkich kulek (obecność kulki pod
który nam powstanie, będzie drzewem, a zdobyte informacje umożliwią zlokalizowanie wszystkich kulek (obecność kulki pod 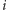 -tym kubkiem to odpowiedź na pytanie
-tym kubkiem to odpowiedź na pytanie ![[i,i + 1]](/math/temat/informatyka/2015/04/19/Kuglarz/4x-3e52682ee12c1e50797610fbf66888e1efb95124-im-33,33,33-FF,FF,FF.gif) ). Zauważmy, że musimy zadać
). Zauważmy, że musimy zadać  pytań, bo każda podpowiedź kuglarza daje nam co najwyżej 1 bit informacji, a musimy zgromadzić
pytań, bo każda podpowiedź kuglarza daje nam co najwyżej 1 bit informacji, a musimy zgromadzić 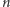 bitów, żeby wyznaczyć lokalizację kulek. Ponadto, kolejność zadawania pytań nie ma znaczenia. Pozostaje kwestia, jak wybierać pytania. Rozważając je w kolejności od najmniejszych kosztów i pomijając pytania, na które znamy odpowiedź, możemy znaleźć strategię dla przykładu o koszcie 7 bajtogroszy (Rys. 2).
bitów, żeby wyznaczyć lokalizację kulek. Ponadto, kolejność zadawania pytań nie ma znaczenia. Pozostaje kwestia, jak wybierać pytania. Rozważając je w kolejności od najmniejszych kosztów i pomijając pytania, na które znamy odpowiedź, możemy znaleźć strategię dla przykładu o koszcie 7 bajtogroszy (Rys. 2).
Zauważmy, że postępując w taki sposób, obliczyliśmy nic innego, jak drzewo rozpinające o minimalnym koszcie dla nieskierowanego grafu pełnego, w którym każda para wierzchołków 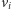 i
i 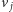 jest połączona krawędzią o wadze
jest połączona krawędzią o wadze 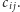 Nasza strategia zachłanna działa dokładnie tak jak algorytm Kruskala, służący do wyznaczania tego drzewa. Ponieważ, jak powiedzieliśmy wyżej, każda strategia zadawania pytań wyznacza nam drzewo rozpinające, zatem, aby znaleźć optymalną strategię, należy znaleźć drzewo rozpinające o minimalnej wadze.
Nasza strategia zachłanna działa dokładnie tak jak algorytm Kruskala, służący do wyznaczania tego drzewa. Ponieważ, jak powiedzieliśmy wyżej, każda strategia zadawania pytań wyznacza nam drzewo rozpinające, zatem, aby znaleźć optymalną strategię, należy znaleźć drzewo rozpinające o minimalnej wadze.
Standardowo robi się to, korzystając właśnie z algorytmu Kruskala lub algorytmu Prima z kolejką priorytetową zrealizowaną za pomocą kopca binarnego. Dla grafu o  wierzchołkach i
wierzchołkach i 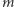 krawędziach oba algorytmy działają w czasie
krawędziach oba algorytmy działają w czasie 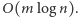 W naszym przypadku mamy jednak do czynienia z grafem pełnym, w którym
W naszym przypadku mamy jednak do czynienia z grafem pełnym, w którym 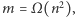 co daje czas
co daje czas 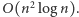 Można ten czas poprawić, zastępując kolejkę priorytetową w algorytmie Prima zwykłą tablicą, w której czas wyszukiwania będzie
Można ten czas poprawić, zastępując kolejkę priorytetową w algorytmie Prima zwykłą tablicą, w której czas wyszukiwania będzie 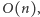 ale czas aktualizacji krawędzi będzie stały. Dzięki temu złożoność rozwiązania zmniejszy się do
ale czas aktualizacji krawędzi będzie stały. Dzięki temu złożoność rozwiązania zmniejszy się do 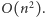
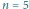 kubków. Koszt
kubków. Koszt 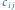 pytania
pytania 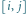 znajduje się na przecięciu wiersza
znajduje się na przecięciu wiersza 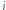 z kolumną
z kolumną 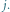
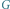 po rozważeniu podpowiedzi o kosztach 1 i 2. Zadajemy pytania odpowiadające pogrubionym krawędziom.
po rozważeniu podpowiedzi o kosztach 1 i 2. Zadajemy pytania odpowiadające pogrubionym krawędziom.