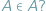
Można spróbować wyobrazić sobie podjęcie próby zdefiniowania czegoś w rodzaju granicy ciągu jednoelementowych zbiorów 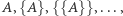ale w ramach teorii zbiorów trudno sobie wyobrazić, jak można by, na przykład, zinterpretować napis zaczynający się i kończący nieskończoną liczbą kropek 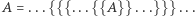wyrażający próbę zapisania takiego zbioru, w dodatku jednoelementowego! Porzućmy ten trop.

Czy jest w ogóle możliwe, żeby było 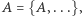czyli żeby zbiór 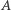miał jako element siebie i oprócz tego być może jeszcze coś? Nazwijmy zbiory, które spełniają taki warunek samowsobnymi. Istnienie takiego fenomenu, jak zbiór mający samego siebie wśród swoich elementów doprowadziło do słynnego paradoksalnego odkrycia Georga Cantora, że nie istnieje zbiór wszystkich zbiorów. Bo gdybyśmy założyli jego istnienie, to dałoby się go podzielić na dwa podzbiory: zbiorów takich, które należą do siebie, czyli są samowsobne, i pozostałych, czyli w miarę normalnych. Zatem istniałby zbiór 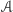złożony z wszystkich zbiorów normalnych, a próba odpowiedzi na pytanie, czy taki zbiór 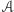należy do siebie, czy też nie, prowadzi do nieuchronnej sprzeczności. Przyjęcie założenia, że 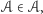oznacza, że 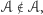bo przecież 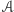składa się właśnie z takich zbiorów, które do siebie nie należą. Zaś przyjęcie założenia, że 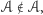oznacza, że 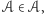bo przecież w 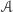są wszystkie zbiory normalne. Otrzymana sprzeczność dowodzi tego, że przyjęte założenie o istnieniu zbioru wszystkich zbiorów jest fałszywe, więc taki zbiór nie może istnieć.

Zauważmy, że w powyższym rozumowaniu w ogóle nie jest istotne, czy istnieje choć jeden taki zbiór samowsobny. Mogłoby się wydawać, że zbiór samowsobny jest jakimś dziwactwem i nikt poważny takiego zbioru zapewne nigdy nie widział.

Nic bardziej mylnego! Ja sam nie tylko taki zbiór widziałem, ale go kiedyś wręcz zrobiłem. No, może przesadziłem, nie sam zbiór, ale jego fizyczny model, niemniej jednak mogłem się na własne oczy przekonać o jego istnieniu i zobaczyć, jak funkcjonuje.

Jestem przekonany, że wielu Czytelników po przeczytaniu poniższej recepty zechce sobie przetestować i powtórzyć mój eksperyment sprzed lat. Wystarczy do tego mieć komputer i system operacyjny, który organizuje pliki w katalogi. No właśnie: co to są katalogi? Wszyscy wiedzą, że to są kolekcje plików i innych katalogów. Innych? A czemu innych? Co by się stało, gdyby w katalogu o nazwie, powiedzmy, A umieścić jako podkatalog właśnie to A? Jak to zrobić? Tak normalnie to się nie da. Żeby podołać temu zadaniu, trzeba dokonać pewnej sztuczki hakerskiej.

Najpierw jednak trzeba zrozumieć, jak komputer definiuje strukturę katalogów i plików. W większości systemów operacyjnych jest tabela adresów, pod którymi znajdują się opisy poszczególnych podkatalogów oraz plików, które w danym katalogu występują. Pod takim typowym adresem będziemy więc mieli nazwę naszego katalogu oraz listę występujących w nim elementów: nadkatalogu, oznaczanego graficznie przez dwie kropki, jego podkatalogów oraz plików. Pliki już takiej listy nie będą zawierały, tylko opis rozmieszczenia kolejnych fragmentów w sektorach dyskowych. Jeśli chcemy wejść do podkatalogu, to pobieramy z listy adres odpowiadający jego nazwie, a następnie pod tym adresem szukamy opisu podanego według tego samego schematu i w odpowiedni sposób uzyskaną informację wyświetlamy. Z tej możliwości korzysta np. system operacyjny, wyświetlając nam zawartość aktualnego katalogu, czy wręcz pokazując od razu całe drzewo katalogów.

Jeśli, znajdując się w jakimś katalogu, chcemy stworzyć jego podkatalog, to nasza lista ulegnie wydłużeniu o nowy element: właśnie wygenerowany przez system operacyjny adres powstającego w tym momencie podkatalogu. Nie wiem, czy już widać, co trzeba zrobić, żeby było śmiesznie. Wystarczy dobrać się do tej listy i podmienić istniejący poprawny adres jednego ze swoich podkatalogów na własny adres katalogu, w którym właśnie przebywamy. Od tego system operacyjny zgłupieje. Nie będzie problemów z dodawaniem nowych plików, czy podkatalogów oraz ich usuwaniem. Jeśli dodamy nowy plik, powiedzmy dane.dat, to zobaczymy go pośród dostępnych elementów, wśród których będzie w szczególności nasz katalog A. Gdy wejdziemy do tego katalogu, wówczas wydłuży się ścieżka o kolejne A, a poza tym będziemy widzieli dokładnie taką samą zawartość, w szczególności dodany przed chwilą plik dane.dat: A stał się elementem samego siebie!

Kłopot się zacznie z chwilą, gdy będziemy próbowali usunąć katalog A. Reakcja komputera zależy tu od tego, jakiego systemu operacyjnego używamy. Zazwyczaj, aby nie zaśmiecać pamięci, systemy operacyjne zanim usuną katalog, usuwają jego zawartość. Niektóre systemy po prostu odmawiają usunięcia niepustego katalogu i każą użytkownikowi samemu o to zadbać, pisząc coś w rodzaju "nie można usunąć katalogu, gdyż nie jest pusty". Pewnie że nie jest, skoro sam do siebie należy! Inne systemy mogą się wręcz zawiesić przy tej akcji, gdyż zgodnie z regułami sztuki próbują przed usunięciem katalogu same usunąć jego zawartość. Orientują się, że katalog nie jest pusty i - co gorsza - zawiera podkatalog, więc najpierw trzeba zapewnić jego opróżnienie. Wchodzą więc pod wskazany adres, a tam widzą, że znowu jest jakiś podkatalog (oczywiście wciąż ten sam!) do usunięcia I tak bez końca.

Właściwie trudno jest dokładnie opisać matematycznie, co się nam udało zrobić, ale przynajmniej widać, jak to działa! Rzadka sytuacja. Zazwyczaj jest na odwrót. Potrafimy coś wyrazić matematycznie, ale nie wiemy, jak to działa i wygląda!

Pozostaje pytanie, jak dokonać tej sztuczki z podmianą adresów. Pozostaje! Ja tego nie ujawnię.