Jajo
Od lat prowadzę ćwiczenia z przedmiotu Języki, Automaty i Obliczenia, w skrócie JAiO, zwanego potocznie „jajo”.
Ma on swój standardowy zbiór zadań, a w nim następujące pytanie-zadanie:
Zadanie. Czy istnieje taki nieregularny język
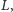 że
że
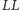 jest
językiem regularnym?
jest
językiem regularnym?
Ma się rozumieć, odpowiedź należy uzasadnić.

Długo by opowiadać, co to są języki, w tym języki regularne, co oznacza mnożenie języków (a tak naprawdę konkatenacja). Oczywiście, nie mogę tego wyjaśnić, bo wówczas Redakcja na pewno nie przyjęłaby mi tego artykułu do numeru pod hasłem „Jakie to proste”.
Jeśli jednak studenci nie wymyślą wystarczająco szybko jakiegoś innego rozwiązania, zaczynam udzielać im podpowiedzi. Tak się miło składa, że po kilku takich podpowiedziach zadanie w sam raz nadaje się do pokazania tutaj.
Wygląda ono wtedy tak:
Zadanie. Czy istnieje zbiór
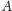 liczb naturalnych, który sam nie jest
prawie-okresowy, ale zbiór
liczb naturalnych, który sam nie jest
prawie-okresowy, ale zbiór
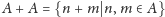 jest
prawie-okresowy?
jest
prawie-okresowy?
Zbiór
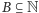 jest okresowy, gdy dla pewnego
jest okresowy, gdy dla pewnego
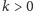 i każdej
liczby naturalnej
i każdej
liczby naturalnej
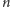 mamy
mamy
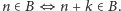 Łatwo sobie taki
zbiór wyobrazić: informacja o tym, które liczby naturalne z przedziału
Łatwo sobie taki
zbiór wyobrazić: informacja o tym, które liczby naturalne z przedziału
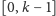 należą do
należą do
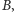 determinuje go całkowicie, bo dalej ten
sam szablon należy/nie należy powtarza się w nieskończoność – trochę
jakby był namalowany na osi przez malarza, który ma wzorzysty wałek do
malowania o obwodzie długości
determinuje go całkowicie, bo dalej ten
sam szablon należy/nie należy powtarza się w nieskończoność – trochę
jakby był namalowany na osi przez malarza, który ma wzorzysty wałek do
malowania o obwodzie długości
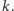 Zbiór jest prawie-okresowy jeśli
można go otrzymać ze zbioru okresowego przez dodanie lub usunięcie
skończenie wielu elementów.
Zbiór jest prawie-okresowy jeśli
można go otrzymać ze zbioru okresowego przez dodanie lub usunięcie
skończenie wielu elementów.
Teraz można już bardzo łatwo udowodnić, że taki zbiór
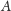 istnieje.
istnieje.
Zacznijmy od
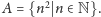 Ten zbiór na pewno nie jest prawie-okresowy,
bo odstępy pomiędzy jego kolejnymi elementami coraz bardziej rosną,
a w zbiorze prawie-okresowym tak nie ma prawa być.
Ten zbiór na pewno nie jest prawie-okresowy,
bo odstępy pomiędzy jego kolejnymi elementami coraz bardziej rosną,
a w zbiorze prawie-okresowym tak nie ma prawa być.
Przyjrzyjmy się teraz
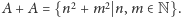
Niewątpliwie
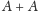 jest prawie-okresowy albo nie jest prawie-okresowy,
ale sprawdzenie, która konkretnie z tych możliwości zachodzi, wymagałoby
chyba trochę pracy. Na szczęście możemy się obyć bez tego.
jest prawie-okresowy albo nie jest prawie-okresowy,
ale sprawdzenie, która konkretnie z tych możliwości zachodzi, wymagałoby
chyba trochę pracy. Na szczęście możemy się obyć bez tego.
W pierwszym przypadku, gdy
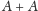 jest prawie-okresowy, żądanym
przykładem jest zbiór
jest prawie-okresowy, żądanym
przykładem jest zbiór
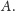
W drugim przypadku żądanym przykładem jest zbiór
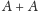 (wówczas nie jest on prawie-okresowy). Zastanówmy się, dlaczego zbiór
(wówczas nie jest on prawie-okresowy). Zastanówmy się, dlaczego zbiór
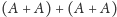 na pewno jest prawie-okresowy.
na pewno jest prawie-okresowy.
Otóż
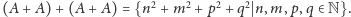 Teraz
przypominamy sobie twierdzenie Lagrange’a, mówiące, że
Teraz
przypominamy sobie twierdzenie Lagrange’a, mówiące, że
Twierdzenie. każda liczba naturalna jest sumą czterech kwadratów liczb naturalnych.
A zatem zdefiniowany w skomplikowany sposób zbiór
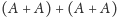 to po prostu
to po prostu
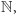 a ten jest oczywiście
prawie-okresowy, a nawet okresowy.
a ten jest oczywiście
prawie-okresowy, a nawet okresowy.
To już koniec dowodu istnienia, i to bez definitywnego wskazania żadnego przykładu.
No właśnie: czy umiesz, Czytelniku, podać konkretny przykład takiego
zbioru
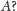 Jeśli nie, kliknij tutaj.
Jeśli nie, kliknij tutaj.
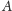 będzie zbiorem tych liczb naturalnych, które nie są
postaci
będzie zbiorem tych liczb naturalnych, które nie są
postaci
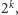 dla
dla
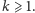 Wówczas
Wówczas
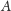 nie jest zbiorem
prawie-okresowym, gdyż odstępy pomiędzy kolejnymi elementami brakującymi w
nie jest zbiorem
prawie-okresowym, gdyż odstępy pomiędzy kolejnymi elementami brakującymi w
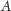 coraz bardziej rosną. Jednak zbiór
coraz bardziej rosną. Jednak zbiór
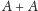 jest prawie-okresowy,
gdyż po prostu
jest prawie-okresowy,
gdyż po prostu
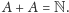 Żeby to zobaczyć weźmy dowolne
Żeby to zobaczyć weźmy dowolne
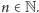 Jeśli
Jeśli
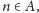 to
to
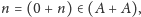 jako że
jako że
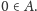 Jeśli zaś
Jeśli zaś
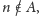 to
to
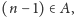 ponieważ nie
istnieją dwie sąsiednie liczby naturalne większe lub równe
ponieważ nie
istnieją dwie sąsiednie liczby naturalne większe lub równe
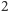 będące
potęgami dwójki. A zatem
będące
potęgami dwójki. A zatem
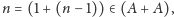 jako, że
jako, że
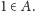 Czytelnik dociekliwy może zauważyć, że taka definicja zbioru
Czytelnik dociekliwy może zauważyć, że taka definicja zbioru
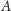 dalece nie jest jedyna możliwa, w szczególności korzystaliśmy
jedynie z bardzo niewielu własności funkcji
dalece nie jest jedyna możliwa, w szczególności korzystaliśmy
jedynie z bardzo niewielu własności funkcji