Ze świata USOS
Część 5 - Oceanarium, czyli o nurkowaniu w otchłani danych
Co wspólnego ma ocean i system USOS? Okazuje się, że znacznie więcej niż tylko literę „o” występującą w obydwu słowach.
Eksploracja oceanu to bardzo wciągający temat. Co znajduje się w otchłani? Źródła minerałów, piękne widoki, dziwaczne stwory? Każdy może bawić się na brzegu w szukanie muszelek, ale aby zejść głębiej i zobaczyć coś, czego nikt inny jeszcze nie widział, potrzebny jest i trening, i specjalistyczny sprzęt.
A co z systemem USOS? Bazy danych tego systemu zawierają wiele informacji. Począwszy od danych, takich jak oceny wystawione studentom, poprzez wyniki ankiet wystawione przez studentów, do wyników z rekrutacji, preferencji w zapisach na przedmioty itp. Początki systemu USOS sięgają roku 1999, przez te kilkanaście lat na niektórych wydziałach zebrał się prawdziwy ocean danych.
Analizując te dane, możemy dowiedzieć się czegoś ciekawego o życiu na uczelni. Oczywiście, co innego będzie ciekawe dla dziekana, co innego dla prowadzącego zajęcia, a jeszcze co innego dla studenta. Zdecydowana większość użytkowników systemu USOS to studenci, dlatego poniżej spojrzymy na ten ocean danych z perspektywy studenta.
Postawimy trzy pytania oraz pokażemy, jak wygląda proces znajdowania odpowiedzi na każde z nich. Każde kolejne pytanie wymagać będzie coraz sprawniejszego aparatu matematycznego i będzie bardziej wymagające obliczeniowo.

Zbieramy muszelki, czyli co znajdziemy na brzegu
Pierwsze pytanie, które często przychodzi na myśl studentom, to Na jakie inne zajęcia zapisana jest ta brunetka, która chodzi ze mną na mikroekonomię? Odpowiedź na takie pytanie jest stosunkowo prosta, o ile ma się bezpośredni dostęp do bazy systemu USOS. Dane są przechowywane w postaci tabel, które odpowiadają relacjom, np. takim jak student X jest zapisany na zajęcia Y.
Aby dowiedzieć się, na jakie inne zajęcia chodzi kolega/koleżanka z naszej
grupy, musimy znać strukturę tych tabel. Najpierw wśród osób
zapisanych z nami na mikroekonomię odnajdziemy interesującą studentkę
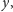 a następnie sprawdzimy, na jakie inne zajęcia
a następnie sprawdzimy, na jakie inne zajęcia
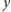 jest
zapisana. Wystarczy dostęp do bazy danych i znajomość języka zapytań
SQL.
jest
zapisana. Wystarczy dostęp do bazy danych i znajomość języka zapytań
SQL.
Snorkeling, czyli pływanie z maską i rurką
Drugie pytanie, które zadamy, dotyczyć będzie mapy „popularności” i „trudności” przedmiotów. Na wielu wydziałach studenci mogą samodzielnie wybierać przedmioty z puli przedmiotów obieralnych. Czyż nie byłoby wspaniale mieć mapę raf i mielizn? Mapę z zaznaczoną zdawalnością dla każdego przedmiotu oraz informacją, jak oceniali go studenci w poprzednich semestrach.
W przeciwieństwie do pierwszego pytania informacja o„popularności”, czy „trudności” przedmiotu nie jest bezpośrednio przechowywana w bazie danych. Te charakterystyki trzeba wyznaczyć na podstawie danych z tabel (nazywanych surowymi, nieprzetworzonymi danymi), tworząc agregaty. Jednym z takich agregatów może być średnia arytmetyczna opinii studentów o przedmiocie. Na podstawie danych z wynikami ankiet możemy obliczyć
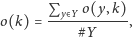 |
gdzie
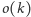 to średnia opinia o przedmiocie
to średnia opinia o przedmiocie
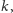
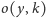 to
opinia o przedmiocie
to
opinia o przedmiocie
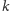 studenta
studenta
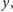
 to zbiór wszystkich
studentów, a symbolem
to zbiór wszystkich
studentów, a symbolem
 oznaczamy liczność zbioru studentów.
W podobny sposób możemy obliczyć procent studentów, którzy zaliczyli
przedmiot
oznaczamy liczność zbioru studentów.
W podobny sposób możemy obliczyć procent studentów, którzy zaliczyli
przedmiot

Obliczywszy dla każdego przedmiotu „popularność” (średnia ocena z ankiet) i „trudność” (zdawalność), możemy te dwie charakterystyki przedstawić na wykresie punktowym. Gdy wybieralnych przedmiotów jest dużo, z wykresu odczytać można więcej niż z tabeli liczb. Poniższy wykres przedstawia sytuacje z Wydziału MIMUW. Każdy przedmiot jest przedstawiony za pomocą pojedynczej kropki. Nazwy przedmiotów usunięto, zamazałyby one cały wykres. Jak widzimy, w ofercie są przedmioty o bardzo wysokiej zdawalności i o niższej zdawalności. Co ciekawe, wydaje się, że zdawalność nie ma większego związku z oceną przedmiotu w ankietach.
Płetwonurkowanie, czyli schodzimy głębiej
Pierwsze z zadanych pytań dotyczyło chwili obecnej. Na jakie przedmioty zapisana jest ta urocza brunetka w tym semestrze? Drugie pytanie dotyczyło danych historycznych, ale wynik rodzi pokusę, by ekstrapolować go na przyszłość. Gdy ja będę wybierał przedmiot na przyszły semestr, jaka jest szansa, że ten przedmiot będzie mnie się podobał i jaka jest szansa, że ja będę miał trudności z zaliczeniem tego przedmiotu?
Chciałbym więc mieć bardziej spersonalizowaną mapę, opartą na danych studentów takich jak ja. Ale, oczywiście, nie ma studentów dokładnie takich jak ja. Studenci są różni i żadnych dwóch nie jest takich samych (prowadzę zajęcia dla studentów od wielu lat i jeszcze nie zdarzyło mi się nie móc rozróżnić dwóch osób). Przewidując więc, jak bardzo dany przedmiot będzie mi się podobał, będę szukał opinii studentów podobnych do mnie. To już głębsze rejony oceanu. Musimy jakoś określić miarę podobieństwa studentów.
Interesuje nas określenie miary niepodobieństwa dwóch studentów,
oznaczmy ich przez
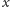 i
i
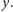 Ich niepodobieństwo będziemy
oznaczać
Ich niepodobieństwo będziemy
oznaczać
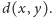 Niektóre algorytmy analizy danych wymagają od
funkcji
Niektóre algorytmy analizy danych wymagają od
funkcji
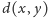 symetrii
symetrii
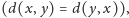 rozróżnialności
rozróżnialności
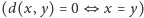 i spełniania warunku trójkąta. Nie zawsze jednak
da się wszystkie te wymagania spełnić. Poniżej opiszemy metody wymagające
jedynie symetrii.
i spełniania warunku trójkąta. Nie zawsze jednak
da się wszystkie te wymagania spełnić. Poniżej opiszemy metody wymagające
jedynie symetrii.
Funkcja
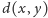 opisuje, jak bardzo studenci
opisuje, jak bardzo studenci
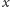 i
i
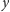 są
niepodobni. Ale można być podobnym/niepodobnym na wiele sposobów. Na
przykład, są podobni, bo chodzili do tej samej szkoły. Podobni, bo mają zbliżone
wyniki z rekrutacji. Podobni, bo na pierwszym semestrze mieli podobne
oceny.
są
niepodobni. Ale można być podobnym/niepodobnym na wiele sposobów. Na
przykład, są podobni, bo chodzili do tej samej szkoły. Podobni, bo mają zbliżone
wyniki z rekrutacji. Podobni, bo na pierwszym semestrze mieli podobne
oceny.
Z tego powodu wygodnie jest definiować podobieństwo przez składowe, np. tak
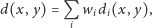 |
gdzie
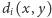 to składowa
to składowa
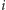 niepodobieństwa, a
niepodobieństwa, a
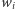 to
waga, z jaką ta składowa wpływa na końcową wartość niepodobieństwa.
Wagi są istotne, ponieważ jeżeli będziemy chcieli przewidzieć, czy jakiś
przedmiot nam się będzie podobał, to będziemy szukać studentów
o podobnych gustach, będziemy więc większą wagę przykładać do składowych
opisujących gusta (np. podobne wybory przedmiotów obieralnych). Jeżeli
interesować nas będzie trudność przedmiotu, to będziemy większą
wagę przykładać do składowych związanych z biegłością w danej
dziedzinie.
to
waga, z jaką ta składowa wpływa na końcową wartość niepodobieństwa.
Wagi są istotne, ponieważ jeżeli będziemy chcieli przewidzieć, czy jakiś
przedmiot nam się będzie podobał, to będziemy szukać studentów
o podobnych gustach, będziemy więc większą wagę przykładać do składowych
opisujących gusta (np. podobne wybory przedmiotów obieralnych). Jeżeli
interesować nas będzie trudność przedmiotu, to będziemy większą
wagę przykładać do składowych związanych z biegłością w danej
dziedzinie.
Mając miarę podobieństwa/niepodobieństwa, możemy chcieć wiedzieć, czy nie da się ze zbioru wszystkich studentów wydzielić podzbiorów studentów „podobnych”. Aby zilustrować to zagadnienie, rozważmy następującą funkcję niepodobieństwa
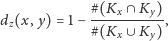 |
gdzie
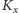 to zbiór przedmiotów, na które zapisany jest student
to zbiór przedmiotów, na które zapisany jest student
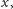
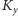 to zbiór przedmiotów, na które zapisany jest student
to zbiór przedmiotów, na które zapisany jest student
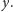

W naszym przykładzie dla Wydziału MIMUW mamy dane dla trzech tysięcy studentów. Macierz niepodobieństwa dla każdej pary studentów ma więc trzy tysiące wierszy i trzy tysiące kolumn. Jak coś zobaczyć w takiej macierzy?
Z pomocą przyjdzie nam technika skalowania wielowymiarowego
(Multidimensional scaling), która pozwala na znalezienie
 -wymiarowej
reprezentacji obiektów dobrze odwzorowującej niepodobieństwo między
obiektami. Dla
-wymiarowej
reprezentacji obiektów dobrze odwzorowującej niepodobieństwo między
obiektami. Dla
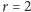 otrzymamy dwuwymiarowy opis dla każdego
studenta, który możliwie dobrze zachowa opisaną funkcję niepodobieństwa.
Przypadek
otrzymamy dwuwymiarowy opis dla każdego
studenta, który możliwie dobrze zachowa opisaną funkcję niepodobieństwa.
Przypadek
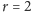 jest interesujący, ponieważ dwa wymiary można
przedstawić na wykresie punktowym.
jest interesujący, ponieważ dwa wymiary można
przedstawić na wykresie punktowym.
Zamieszczony obok wykres przedstawia wynik skalowania dla wspomnianych trzech tysięcy studentów. Każdy punkt odpowiada jednemu studentowi. Punkty bliskie sobie powinny odpowiadać studentom podobnym według zadanej miary niepodobieństwa, a punkty dalekie od siebie odpowiadać powinny studentom niepodobnym.
Jak widzimy, punkty nie tworzą jednej chaotycznej chmury, ale odnaleźć można podgrupy studentów wybierających podobne przedmioty! Niektóre z nich odpowiadają specjalnościom, widać jednak, że granice między grupami nie są ostre i wielu studentów jest „gdzieś pomiędzy”.
Co jeszcze możemy zrobić z macierzą niepodobieństwa? Wykorzystajmy
ją do oszacowania/odgadnięcia
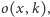 czyli opinii studenta
czyli opinii studenta
 o przedmiocie
o przedmiocie
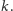
Przyjmując, że opinia studenta
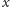 będzie podobna do opinii studentów
podobnych do
będzie podobna do opinii studentów
podobnych do
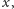 mogę np. uśrednić opinię 10 studentów najbardziej
podobnych do
mogę np. uśrednić opinię 10 studentów najbardziej
podobnych do
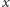 lub studentów o niepodobieństwie mniejszym od
lub studentów o niepodobieństwie mniejszym od
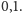 W wielu przypadkach dobre wyniki daje uśrednianie opinii wielu
studentów poprzez ważenie głosu studenta
W wielu przypadkach dobre wyniki daje uśrednianie opinii wielu
studentów poprzez ważenie głosu studenta
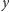 w zależności od tego,
jak bardzo jest on podobny do studenta
w zależności od tego,
jak bardzo jest on podobny do studenta
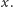 Im bardziej podobny, tym
ważniejsza będzie jego opinia.
Im bardziej podobny, tym
ważniejsza będzie jego opinia.
Tak otrzymujemy wzór na ocenę opinii studenta
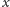 o przedmiocie
o przedmiocie
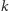 jako ważoną średnią opinii innych studentów
jako ważoną średnią opinii innych studentów
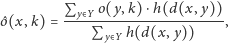 |
gdzie
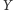 to zbiór wszystkich studentów,
to zbiór wszystkich studentów,
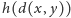 to funkcja
określająca, jak niepodobieństwo studentów
to funkcja
określająca, jak niepodobieństwo studentów
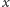 i
i
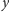 przekłada się
na wagę opinii studenta
przekłada się
na wagę opinii studenta
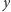 w przewidywaniu gustów studenta
w przewidywaniu gustów studenta
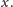 Jednym z częstych wyborów jest
Jednym z częstych wyborów jest
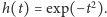

Możemy teraz oszacować opinię studenta
 o każdym z przedmiotów.
Podobnie możemy oszacować jego szanse zaliczenia przedmiotu i przedstawić
mu bardziej spersonalizowaną mapę „trudność–popularność”.
o każdym z przedmiotów.
Podobnie możemy oszacować jego szanse zaliczenia przedmiotu i przedstawić
mu bardziej spersonalizowaną mapę „trudność–popularność”.
Przedstawiony wzór na „średnią” można dowolnie modyfikować. Na przykład, zamiast wyznaczania średniej zdawalności możemy wyznaczyć rozkład ocen wśród podobnych studentów ważony podobieństwem do wybranego studenta.
Zobaczmy, jak to wygląda na konkretnym przykładzie. Weźmy pod lupę
przedmiot Pakiety statystyczne: R i SAS, który prowadzę. Następnie wybierzmy
studenta o wdzięcznym identyfikatorze
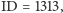 który na ten
przedmiot jeszcze nie uczęszczał, i zobaczmy, czy wśród studentów, którzy
ten przedmiot realizowali, ci podobni do
który na ten
przedmiot jeszcze nie uczęszczał, i zobaczmy, czy wśród studentów, którzy
ten przedmiot realizowali, ci podobni do
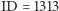 otrzymywali lepsze czy
gorsze oceny.
otrzymywali lepsze czy
gorsze oceny.
Na poniższym wykresie przedstawiono procent studentów, którzy otrzymali
określoną ocenę z przedmiotu Pakiety statystyczne: R i SAS. Dolny pasek
opisuje sytuacje wszystkich studentów realizujących ten przedmiot. Pasek na
górze jest ważony podobieństwem do
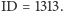 Okazuje się, że
„podobni” studenci mają częściej lepsze oceny. Również szanse niezaliczenia
(oznaczone jako NK) są niższe niż w przypadku „losowego” studenta. Nic,
tylko się zapisywać!
Okazuje się, że
„podobni” studenci mają częściej lepsze oceny. Również szanse niezaliczenia
(oznaczone jako NK) są niższe niż w przypadku „losowego” studenta. Nic,
tylko się zapisywać!

Na podobnej zasadzie działają systemy rekomendacyjne sugerujące zakup książki w księgarni internetowej czy proponujące film do obejrzenia. I podobnie jak w przypadku książek czy filmów, nie ma gwarancji, że to, co podobało się osobom o podobnych profilach do naszego, spodoba się również nam. Gwarancji nie ma, ale czasem nawet informacja „niepewna” może być użyteczna.
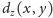 może być równe
może być równe
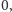 nawet gdy
nawet gdy
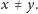 Wystarczy, by
Wystarczy, by
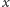 i
i
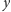 byli zapisani na te same
przedmioty. Trzeba z tym żyć albo zmienić funkcję niepodobieństwa.
byli zapisani na te same
przedmioty. Trzeba z tym żyć albo zmienić funkcję niepodobieństwa.
 oznacza szacowanie opinii. Aby poznać
prawdziwą opinię
oznacza szacowanie opinii. Aby poznać
prawdziwą opinię
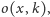 student
student
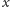 musiałby się na przedmiot
musiałby się na przedmiot
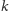 zapisać, a później musiałby go ocenić.
zapisać, a później musiałby go ocenić.